Session 07-03 - Combinatorics & Counting
Section 07: Probability & Statistics
Entry Quiz - 10 Minutes
Quick Review from Session 07-02
Test your understanding of Basic Probability
If \(P(A) = 0.4\) and \(P(B) = 0.3\) and A and B are independent, find \(P(A \cap B)\).
Use the complement rule: If \(P(\text{rain}) = 0.25\), find \(P(\text{no rain})\).
If \(P(A) = 0.5\), \(P(B) = 0.4\), and \(P(A \cap B) = 0.2\), find \(P(A \cup B)\).
Are events A and B from question 3 independent? Why or why not?
Homework Discussion - 12 Minutes
Your Questions from Session 07-02
Let’s clarify notation before counting gets harder.
- Independent vs mutually exclusive events
- Complement strategy for “at least one”
- Translating set notation into plain language
Learning Objectives
What You’ll Master Today
- Apply the fundamental counting principle for sequential events
- Calculate permutations: \(P(n,r) = \frac{n!}{(n-r)!}\)
- Calculate combinations: \(C(n,r) = \binom{n}{r} = \frac{n!}{r!(n-r)!}\)
- Distinguish when order matters vs. doesn’t matter
- Connect counting to probability calculations
. . .
Combinatorics is essential for calculating probabilities on the exam!
Part A: Fundamental Counting Principle
Sequential Choices
If you make sequential choices with \(n_1, n_2, ..., n_k\) options:
\[\text{Total possibilities} = n_1 \times n_2 \times ... \times n_k\]
. . .
Example: Creating an outfit
- 4 shirts
- 3 pairs of pants
- 2 pairs of shoes
. . .
Total outfits: \(4 \times 3 \times 2 = 24\)
License Plate Example
A license plate has:
- 3 letters (A-Z, 26 options each)
- 4 digits (0-9, 10 options each)
. . .
Question: How many different plates are possible?
. . .
With repetition allowed: \[26 \times 26 \times 26 \times 10 \times 10 \times 10 \times 10 = 26^3 \times 10^4 = 175,760,000\]
. . .
Without repetition: \[26 \times 25 \times 24 \times 10 \times 9 \times 8 \times 7 = 78,624,000\]
Factorial Notation
Definition: Factorial
\[n! = n \times (n-1) \times (n-2) \times \dots \times 1\]
Special cases: \(0! = 1\) and \(1! = 1\)
. . .
Examples:
- \(5! = 5 \times 4 \times 3 \times 2 \times 1 = 120\)
- \(3! = 3 \times 2 \times 1 = 6\)
- \(10! = 3,628,800\)
Part B: Permutations
When Order Matters
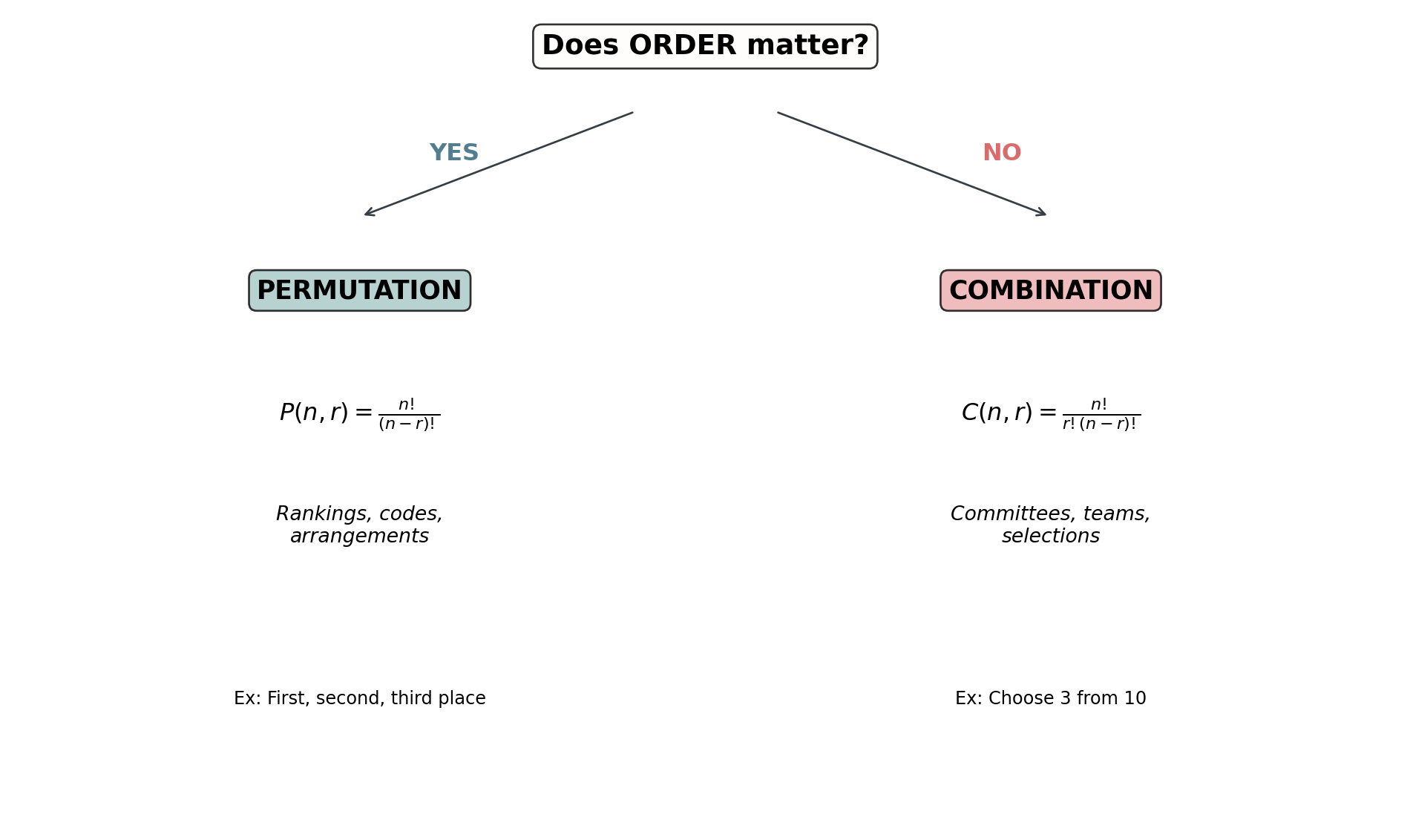
Definition: Permutation
A permutation is an arrangement of objects where order matters.
. . .
\[P(n,r) = \frac{n!}{(n-r)!}\]
. . .
= Number of ways to arrange \(r\) objects from \(n\) distinct objects
. . .
Example: How many ways can 3 people win gold, silver, and bronze from 8 competitors?
. . .
\[P(8,3) = \frac{8!}{5!} = \frac{8 \times 7 \times 6 \times 5!}{5!} = 8 \times 7 \times 6 = 336\]
Permutation Examples
Example 1: Arrange all letters in “MATH”
. . .
\[P(4,4) = 4! = 24 \text{ arrangements}\]
. . .
Example 2: How many 4-digit PINs with no repeated digits?
. . .
\[P(10,4) = \frac{10!}{6!} = 10 \times 9 \times 8 \times 7 = 5,040\]
. . .
Example 3: A president, VP, and treasurer from 12 candidates?
. . .
\[P(12,3) = 12 \times 11 \times 10 = 1,320\]
Part C: Combinations
When Order Doesn’t Matter
Definition: Combination
A combination is a selection of objects where order doesn’t matter.
. . .
\[C(n,r) = \binom{n}{r} = \frac{n!}{r!(n-r)!}\]
. . .
= Number of ways to choose \(r\) objects from \(n\) distinct objects
. . .
Insight: Each combination corresponds to \(r!\) permutations
. . .
\[C(n,r) = \frac{P(n,r)}{r!}\]
Combination Examples
Example 1: Choose 3 students from 10 for a committee
. . .
\[C(10,3) = \binom{10}{3} = \frac{10!}{3! \cdot 7!} = \frac{10 \times 9 \times 8}{3 \times 2 \times 1} = 120\]
. . .
Example 2: Choose 5 cards from a 52-card deck
. . .
\[C(52,5) = \binom{52}{5} = \frac{52!}{5! \cdot 47!} = \frac{52 \times 51 \times 50 \times 49 \times 48}{120} = 2,598,960\]
Decision Tree
If order matters, use permutations. If not, use combinations.
Quick Check - 6 Minutes
Decide the Method First
Work individually
For each situation, write either permutation or combination and compute:
- Choose 2 class representatives from 11 students.
- Assign president and vice president from 11 students.
- Number of 3-digit PINs from digits 0-9 (repetition allowed).
Break - 10 Minutes
Part D: Combinatorics in Probability
Connecting Counting to Probability
For equally likely outcomes:
\[P(A) = \frac{\text{Number of favorable outcomes}}{\text{Total number of outcomes}}\]
. . .
- Counting helps us find both numbers!
- Let’s look at some examples.
. . .
Question: Probability of being dealt exactly 2 hearts in a 5-card hand?
Example: Card Probability
Favorable: Choose 2 hearts from 13, AND 3 non-hearts from 39
. . .
\[\binom{13}{2} \times \binom{39}{3} = 78 \times 9,139 = 712,842\]
. . .
Total outcomes: Choose any 5 cards from 52
\[\binom{52}{5} = 2,598,960\]
. . .
Probability: \(P(\text{exactly 2 hearts}) = \frac{712,842}{2,598,960} \approx 0.274\)
Example: Committee Selection
A committee of 4 must be chosen from 6 men and 5 women.
Question: Probability that the committee has exactly 2 women?
- Total ways to form committee: \(\binom{11}{4} = 330\)
- Ways to get exactly 2 women: \(\binom{5}{2} \times \binom{6}{2} = 10 \times 15 = 150\)
- Probability: \(P(\text{exactly 2 women}) = \frac{150}{330} = \frac{5}{11} \approx 0.455\)
. . .
Do you see a pattern here?
Example: Quality Control
Box contains 20 items: 4 are defective. We select 3 items randomly:
- \(P(\text{none defective})\)
. . .
\[P = \frac{\binom{16}{3}}{\binom{20}{3}} = \frac{560}{1140} = \frac{14}{28.5} \approx 0.491\]
. . .
- \(P(\text{at least one defective})\)
. . .
\[P = 1 - P(\text{none}) = 1 - 0.491 = 0.509\]
Part E: Pascal’s Triangle
A Shortcut for Binomial Coefficients

. . .
You’ve been computing \(\binom{n}{r}\) all session — for card hands, committees, and defective items. Pascal’s triangle arranges all these values in a pattern that makes them easy to look up and verify.
Pascal’s Triangle
The recursive property — each entry is the sum of the two above it:
\[\binom{n}{r} + \binom{n}{r+1} = \binom{n+1}{r+1}\]
. . .
Why this matters: Instead of computing \(\binom{5}{2} = \frac{5!}{2!\,3!}\) from scratch, find row \(n=5\) and look up the entry for \(r=2\) → 10. This saves time when verifying combination calculations.
. . .
Or you use your calculator or R to compute \(\binom{n}{r}\).
Guided Practice - 20 Minutes
Practice Problems
Work in pairs
Problem 1: A password must have 3 letters followed by 2 digits. a) How many passwords are possible (with repetition)? b) How many if no repetition is allowed?
Problem 2: From 8 candidates, we select a president, VP, secretary, and treasurer. How many ways?
Problem 3: A lottery requires choosing 6 numbers from 49. How many possible combinations?
Chained Exam Mini-Problem
Work individually, then compare
A committee of 4 is chosen from 10 people, including 3 finance majors.
- Compute total possible committees.
- Compute committees with exactly 2 finance majors.
- Use (a) and (b) to compute the probability of exactly 2 finance majors.
Training Tasks I
Work individually
An ice cream shop offers 12 flavors. You order a bowl with 3 scoops.
- How many bowls are possible if you choose 3 different flavors and the order of scoops doesn’t matter?
- Your friend orders a cone where the stacking order matters. How many cones with 3 different flavors are possible?
- What is the probability that a randomly chosen bowl (from part a) contains your two favorite flavors?
Training Tasks II
Work individually
A class has 15 students: 9 from Business and 6 from Economics. The professor randomly forms a project team of 5 students.
- How many possible teams are there?
- How many teams have exactly 3 Business and 2 Economics students?
- What is the probability that the team has exactly 3 Business and 2 Economics students?
Coffee Break - 10 Minutes
Collaborative Problem-Solving - 20 Minutes
Group Challenge: Event Planning
Think individually, then work in groups
An event team must choose from 9 volunteers:
- A chairperson, vice-chairperson, and treasurer.
- A separate 4-person logistics team.
- The probability that exactly 2 of 5 selected panelists are international students, if 7 of 18 applicants are international.
For each part, explain clearly whether order matters and why.
Counting Principle: Travel Routes
Work in pairs
A sales representative must visit 3 cities. She can travel:
- From her office to City A by 4 routes
- From City A to City B by 3 routes
- From City B to City C by 2 routes
- How many different travel plans are possible?
- If she must also return from City C to her office and there are 3 return routes, how many round trips are possible?
- If one route from office to City A is closed, how many travel plans remain for part (a)?
Permutations vs. Combinations: Bookshelf
Work in pairs
A student has 8 different textbooks.
- How many ways can she arrange all 8 books on a shelf?
- How many ways can she choose 4 books to take on a trip?
- She wants to stack her 4 chosen books in a pile on her desk. How many different stacks are possible?
- Explain why (b) and (c) give different answers.
Probability with Combinatorics: Raffle Draw
Work individually, then compare
A company raffle has 30 tickets. You bought 4 tickets. Three winning tickets are drawn at random.
- How many ways can the 3 winning tickets be drawn?
- How many ways can all 3 winners come from your tickets?
- What is the probability that you win all 3 prizes?
- What is the probability that you win exactly 1 prize?
Mixed Problem: Digital Security
Work in groups
A company assigns 6-character access codes using digits 0-9 and uppercase letters A-Z (36 characters total).
- How many codes are possible if repetition is allowed?
- How many codes are possible if no character may repeat?
- A valid code must contain exactly 2 digits and 4 letters (no repetition, order matters). How many valid codes are there?
- If a code is generated at random (under the rules of part c), what is the probability that the two digits are adjacent?
Complement Strategy: Defective Parts
Work individually
A shipment contains 25 items, of which 5 are defective. A quality inspector selects 4 items at random.
- What is the probability that none of the selected items are defective?
- What is the probability that at least one selected item is defective?
- What is the probability that exactly 2 selected items are defective?
Final Assessment - 5 Minutes
Exit Ticket
Work individually
- How many 4-letter codes can be formed from 26 letters with repetition?
- How many ways to choose 3 students from 12?
- Which uses combinations: “arrange” or “choose”?
Wrap-Up & Key Takeaways
Today’s Essential Concepts
- Counting principle: Multiply choices for sequential events
- Factorial: \(n! = n \times (n-1) \times ... \times 1\)
- Permutations: Order matters - \(P(n,r) = \frac{n!}{(n-r)!}\)
- Combinations: Order doesn’t matter - \(C(n,r) = \frac{n!}{r!(n-r)!}\)
- Key question: Does the order of selection matter?
Next Session Preview
Coming Up: Conditional Probability
- Conditional probability: \(P(A|B)\)
- Multiplication rule
- Tree diagrams
- Independence revisited
. . .
Complete Tasks 07-03:
- Practice permutation and combination calculations
- Solve probability problems using combinatorics
