Session 03-02 - Linear Functions & Economic Applications
Section 03: Functions as Business Models
Entry Quiz - 10 Minutes
Review from Session 03-01
Work individually, then exchange with your neighbor for peer review
Given \(f(x) = 2x - 8\), find:
- \(f(5)\)
- The value of \(x\) when \(f(x) = 10\)
A company has cost function \(C(x) = 1000 + 25x\) and revenue function \(R(x) = 40x\). Find the break-even point.
Does the equation \(x = y^2 - 4\) represent \(y\) as a function of \(x\)? Explain using the vertical line test.
Homework Discussion - 20 Minutes
Forms of Linear Functions
Slope-Intercept Form
The most common form: y = mx + b
- m: slope (rate of change/ marginal change)
- Positive: increasing function
- Negative: decreasing function
- Zero: horizontal line
- b: y-intercept (starting value/ base value)
- Value when \(x = 0\)
- Often represents fixed costs or initial values
Point-Slope Form
Useful when you know a point and the slope
\[y - y_1 = m(x - x_1)\]
- \((x_1, y_1)\): known point on the line
- \(m\): slope of the line
- When to use:
- Given one data point and rate of change
- Finding equation from two points
- Modeling from observed data
Example: Price Change
We have already done this by intuition, now let’s formalize it
A product costs €50 when producing 100 units. Each additional unit reduces the price by €0.20.
. . .
\[p - 50 = -0.20(x - 100)\] \[p = -0.20x + 20 + 50\] \[p = -0.20x + 70\]
Parallel and Perpendicular Lines
Critical for understanding related economic functions
- Parallel lines: Same slope (\(m_1 = m_2\))
- Example: Two companies with same variable cost per unit
- Different fixed costs create parallel cost functions
- Perpendicular lines: \(m_1 \cdot m_2 = -1\)
- Less common in economics
- Sometimes seen in utility theory
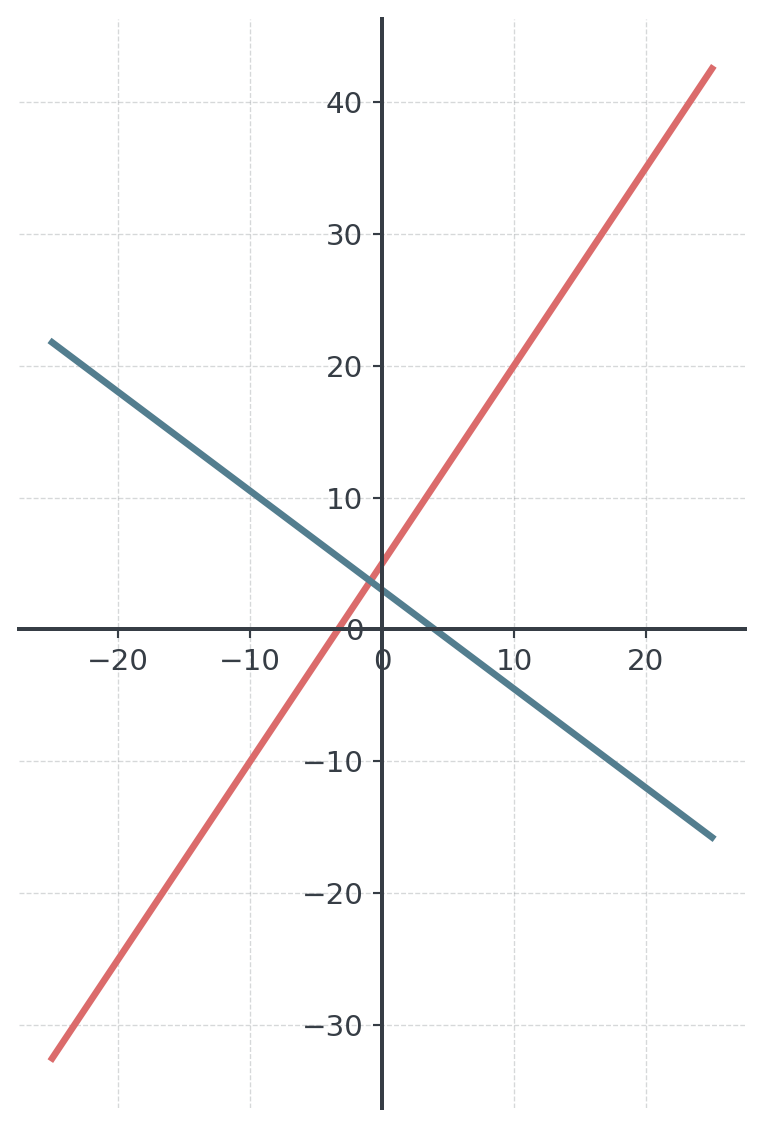
Visual: Perpendicular Lines
Business Example: Competing Firms
- Company A: \(C_A(x) = 3x + 1000\)
- Company B: \(C_B(x) = 3x + 1500\)
. . .
Question: What do you see here?
. . .
- Same variable cost (€3/unit), different fixed costs
- Parallel cost functions!
Visual: Competing Firms
Quick Practice - 5 Minutes
Let’s apply our new knowledge
1. Given: \(f(x) = -2x + 7\)
- What is the slope?
- What is the y-intercept?
- Is the function increasing or decreasing?
2. A profit function passes through (50, 2000) with a slope of 30.
- Write the profit function in point-slope form
- Convert to slope-intercept form
- What does the slope represent in this business context?
Break - 10 Minutes
Supply and Demand Functions
Understanding Demand
Demand shows how quantity purchased depends on price
- Generally decreasing: Higher price → Lower quantity
- Linear demand: \(Q_d = a - bp\) where \(p\) is price
- \(a\): maximum quantity (when price = 0)
- \(b\): sensitivity to price changes
- Alternative form: \(p = c - dQ_d\)
- Express price in terms of quantity
Example: Coffee Shop Demand
Daily coffee demand: \(Q_d = 500 - 50p\)
- At €0: Would “sell” 500 cups (theoretical maximum)
- At €10: Would sell 0 cups
- At €4: \(Q_d = 500 - 50(4) = 300\) cups
. . .
Question: Who can draw this?
Understanding Supply
Supply shows how quantity produced depends on price
- Generally increasing: Higher price → Higher quantity
- Linear supply: \(Q_s = -c + dp\) where \(p\) is price
- Often passes through origin or has positive intercept
- \(d\): production response to price
Example: Coffee Shop Supply
Daily coffee supply: \(Q_s = -100 + 100p\)
- Below €1: No supply (not profitable)
- At €3: \(Q_s = -100 + 100(3) = 200\) cups
- At €5: \(Q_s = -100 + 100(5) = 400\) cups
. . .
Question: Anyone who can draw this?
Market Equilibrium
Equilibrium occurs where supply equals demand
\[Q_d = Q_s\]
- Equilibrium price (\(p^*\)): Market-clearing price
- Equilibrium quantity (\(Q^*\)): Amount actually traded
- Graphically: Intersection of supply and demand curves
- Economically: No shortage or surplus
Finding Equilibrium Example
Using our coffee shop:
- Demand: \(Q_d = 500 - 50p\)
- Supply: \(Q_s = -100 + 100p\)
. . .
At €4 per cup, suppliers want to sell exactly 300 cups, and consumers want to buy exactly 300 cups. The market clears!
. . .
Question: How would this look like if we graph it?
Guided Practice - 25 Minutes
Individual Exercise Block I
Work alone for 10 minutes, then discuss
- Convert between forms:
- Given two points (2, 10) and (5, 19), find the slope-intercept form
- Rewrite \(2x - 3y = 12\) in slope-intercept form
- A local bakery faces:
- Demand: \(Q_d = 200 - 10p\) (loaves per day)
- Supply: \(Q_s = 50 + 15p\) (loaves per day)
Individual Exercise Block II
Work alone for 5 minutes, then discuss
- Two taxi companies have cost functions:
- Company A: \(C_A(x) = 5 + 2x\) (x in km)
- Company B: \(C_B(x) = 2 + 2.5x\)
- Which company is cheaper for a 5km ride? A 10km ride?
- At what distance do they cost the same?
- What do the parameters represent economically?
Coffee Break - 15 Minutes
Cost-Volume-Profit Analysis
The CVP Framework
Understanding the relationship between costs, volume, and profit
. . .
- Fixed Costs (FC): Independent of production volume
- Variable Costs (VC): Change with production volume
- Total Costs: \(TC = FC + VC \times Q\)
- Revenue: \(R = P \times Q\) (Price × Quantity)
- Profit: \(\Pi = R - TC = PQ - (FC + VC \times Q)\)
- Contribution Margin: \(CM = P - VC\)
. . .
Puzzled why we use a different notation now? Don’t worry, keep in mind that in mathematics you can assign any variable to any quantity, as long as you are consistent.
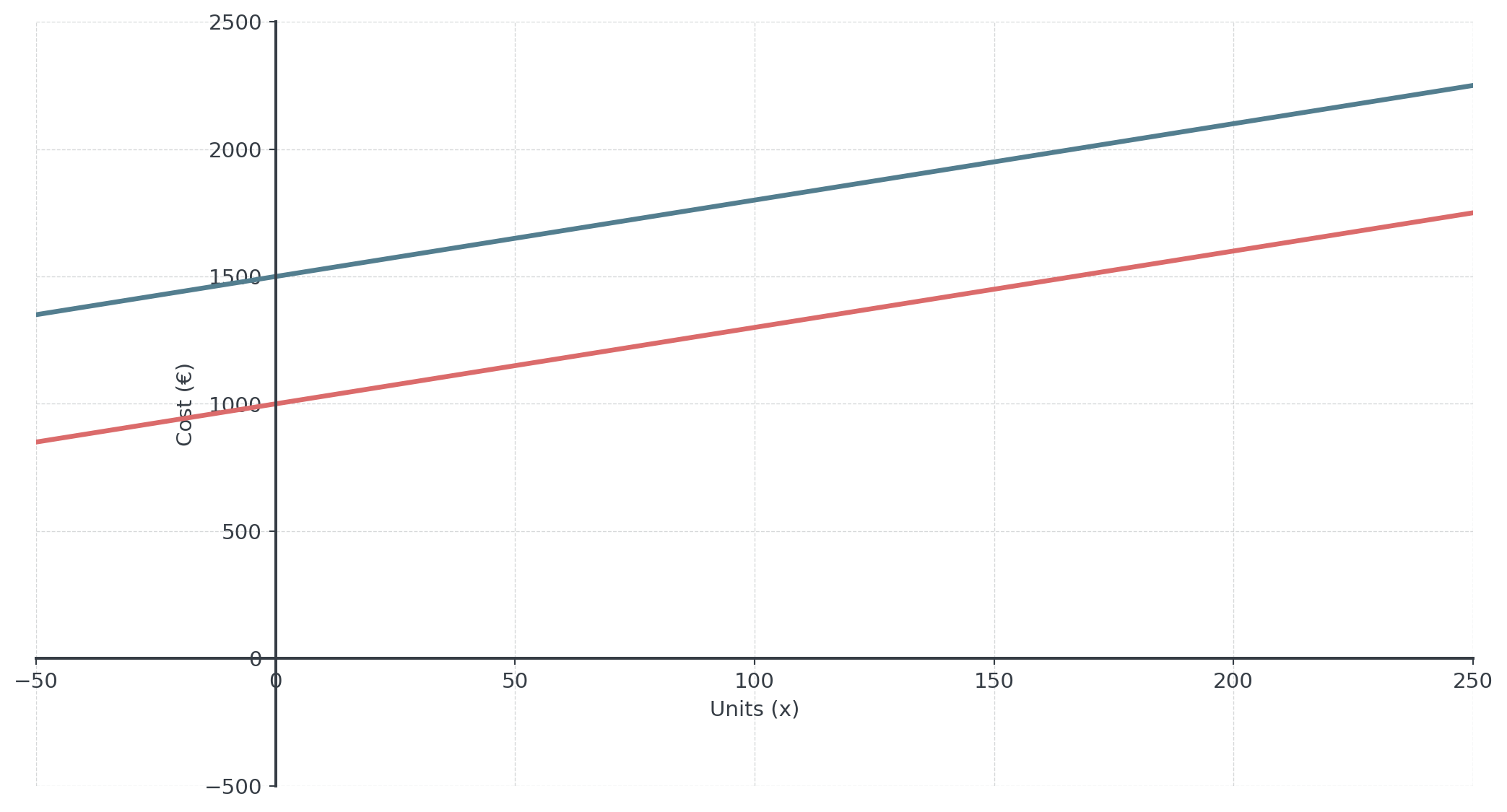
CVP Example: Restaurant
A restaurant has:
- Fixed costs: €8,000/month (rent, salaries)
- Variable cost per meal: €12 (ingredients, utilities)
- Selling price per meal: €25
- Contribution margin: €25 - €12 = €13 per meal
- Break-even quantity: \(Q_{BE} = \frac{8000}{13} \approx 616\) meals
- For 1000 meals: \(\Pi = 1000(13) - 8000 = 5,000\) profit
- Margin of safety: \(1000 - 616 = 384\) meals above break-even
Linear Modeling from Data
Creating Linear Models
From real-world observations to mathematical functions
Steps to create a linear model:
- Identify the variables (dependent vs. independent)
- Plot the data points (if possible)
- Calculate the slope between points
- Use point-slope form to find equation
- Interpret parameters in context
Example: Sales Forecasting
Monthly sales data:
| Month | Units Sold |
|---|---|
| 1 | 120 |
| 2 | 135 |
| 3 | 150 |
| 4 | 165 |
- Is there a linear trend? +15 units per month
- Using month 1: \(S - 120 = 15(m - 1)\)
- Simplified: \(S(m) = 15m + 105\)
Depreciation Models
Linear Depreciation
Straight-line depreciation: Constant value loss over time
\[V(t) = V_0 - dt\]
Where:
- \(V(t)\): Value at time \(t\)
- \(V_0\): Initial value
- \(d\): Depreciation rate per period
- Useful life: \(n = \frac{V_0}{d}\) periods
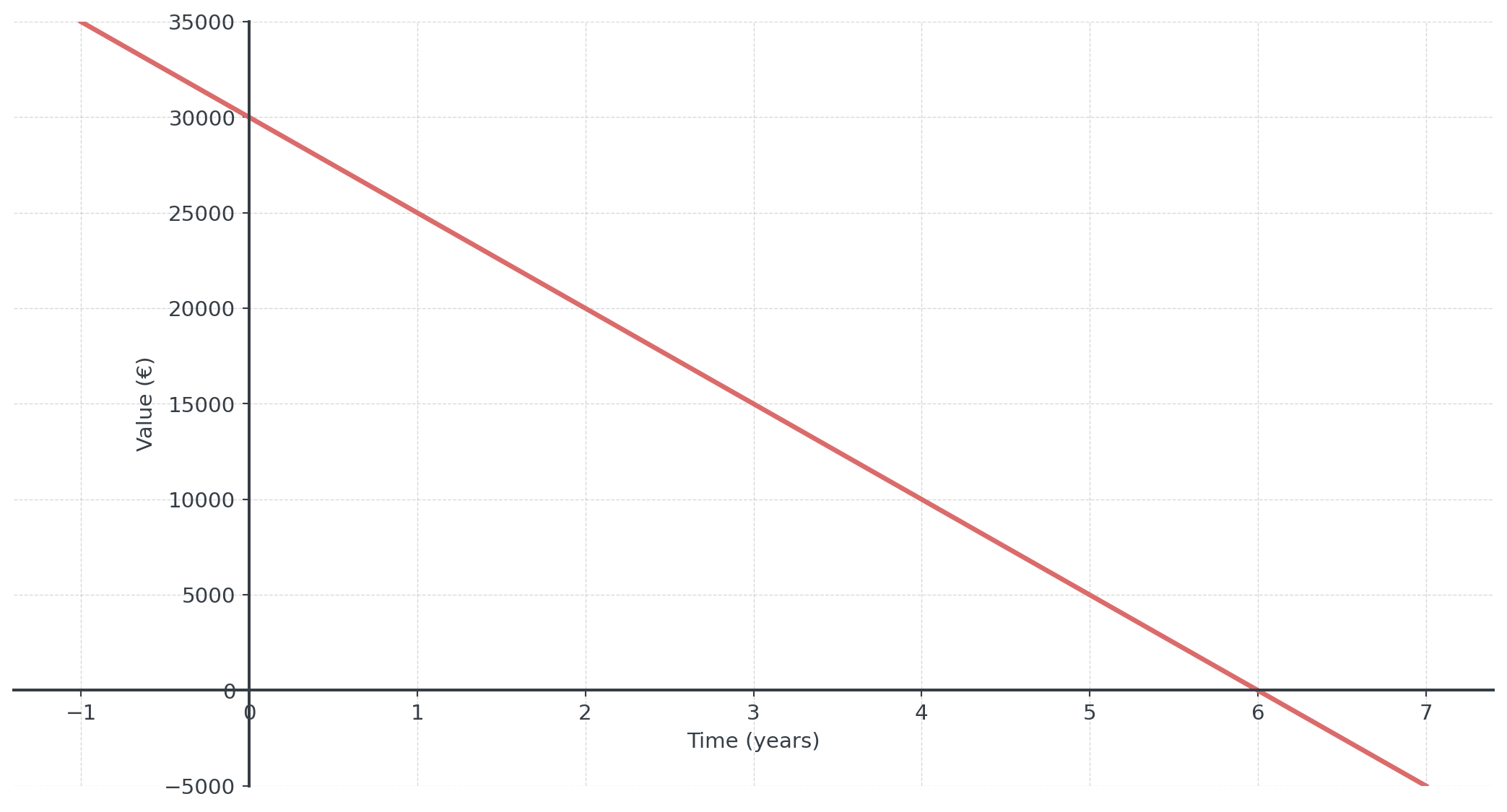
Example: Company Vehicle
A company buys a new vehicle
- Purchase price: €30,000
- Depreciation: €5,000 per year
- \(V(t) = 30000 - 5000t\)
- After 4 years: \(V(4) = 30000 - 20000 = 10,000\)
- Fully depreciated after 6 years
. . .
Important in financial planning and asset management!
Depreciation Visualization
Collaborative Problem-Solving - 30 Minutes
Market Analysis Scenario
The Scenario: Local Organic Farm Market
A new organic farm is entering the local market. Research shows:
- Current market demand: \(Q_d = 1000 - 40p\) (kg per week)
- Current market supply (other farms): \(Q_s = 200 + 20p\) (kg per week)
- The new farm can supply: \(Q_{new} = 50 + 10p\) (kg per week)
- The new farm has fixed costs of €500/week and variable costs of €8/kg
Your Tasks:
Work in groups of 3-4 students
Find the current market equilibrium (before the new farm)
Find the new market equilibrium after the farm enters
Determine if the new farm will be profitable at the new equilibrium price
What minimum price does the new farm need to break even if they sell their equilibrium quantity?
If the new farm could convince consumers that their organic produce is superior, shifting demand to \(Q_d = 1200 - 40p\), how would this affect their profitability?
Wrap-Up & Exit Ticket
Key Takeaways
- Linear functions model constant rates of change
- Supply and demand intersect at market equilibrium
- CVP analysis reveals break-even points
- Contribution margin shows unit profitability
- Real data can be modeled with linear approximations
Final Assessment
5 minutes - Individual work
A smartphone manufacturer has:
- Demand function: \(Q_d = 800 - 2p\)
- Supply function: \(Q_s = 100 + 3p\)
- Fixed costs: €50,000
- Variable costs: €80 per unit
- Find the market equilibrium price and quantity
- Calculate the manufacturer’s profit at equilibrium
- What is the contribution margin per unit?
Next Session Preview
Session 03-03: Quadratic Functions & Basic Optimization
- Parabolas and their properties
- Finding vertex using \(x = -\frac{b}{2a}\)
- Maximum and minimum values
- Revenue optimization with price-dependent demand
- Projectile motion applications
. . .
Homework Assignment: Complete Tasks 03-02!
