Session 05-05 - Graphical Calculus Mastery

Section 05: Differential Calculus

Entry Quiz - 10 Minutes

Quick Review from Session 05-04

Test your understanding of chain rule and implicit differentiation

1. Differentiate \(f(x) = (2x^3 - 5)^4\) using the chain rule.

2. Find \(\frac{dy}{dx}\) if \(x^2 + xy = 10\).

3. If \(f'(3) = 0\), what does this tell about the graph of \(f(x)\) at \(x = 3\)?

Homework Discussion - 15 Minutes

Your questions from Session 05-04

What questions do you have regarding the previous session?

Learning Objectives

What You’ll Master Today

• Sketch \(f'(x)\) from the graph of \(f(x)\) by analyzing slopes
• Determine properties of \(f(x)\) from the graph of \(f'(x)\)
• Understand concavity through second derivatives \(f''(x)\)
• Identify critical points and their classification
• Find inflection points where concavity changes
• Master visual analysis - a heavily tested exam skill!

. . .

NoteKey Insight

Being able to translate between graphs of \(f\), \(f'\), and \(f''\) is one of the most important visual skills in calculus and frequently tested!

Part A: From Function to Derivative

Understanding the Derivative Graph

The graph of \(f'(x)\) shows the slope of \(f(x)\) at each point.

. . .

What to look for in \(f(x)\):

• Where \(f\) is increasing → \(f'(x) > 0\) (derivative is positive)
• Where \(f\) is decreasing → \(f'(x) < 0\) (derivative is negative)
• Where \(f\) has a horizontal tangent → \(f'(x) = 0\) (crosses x-axis)
• Where \(f\) is steep → \(|f'(x)|\) is large
• Where \(f\) is flat → \(|f'(x)|\) is small

. . .

This shouldn’t be too complicated, right?

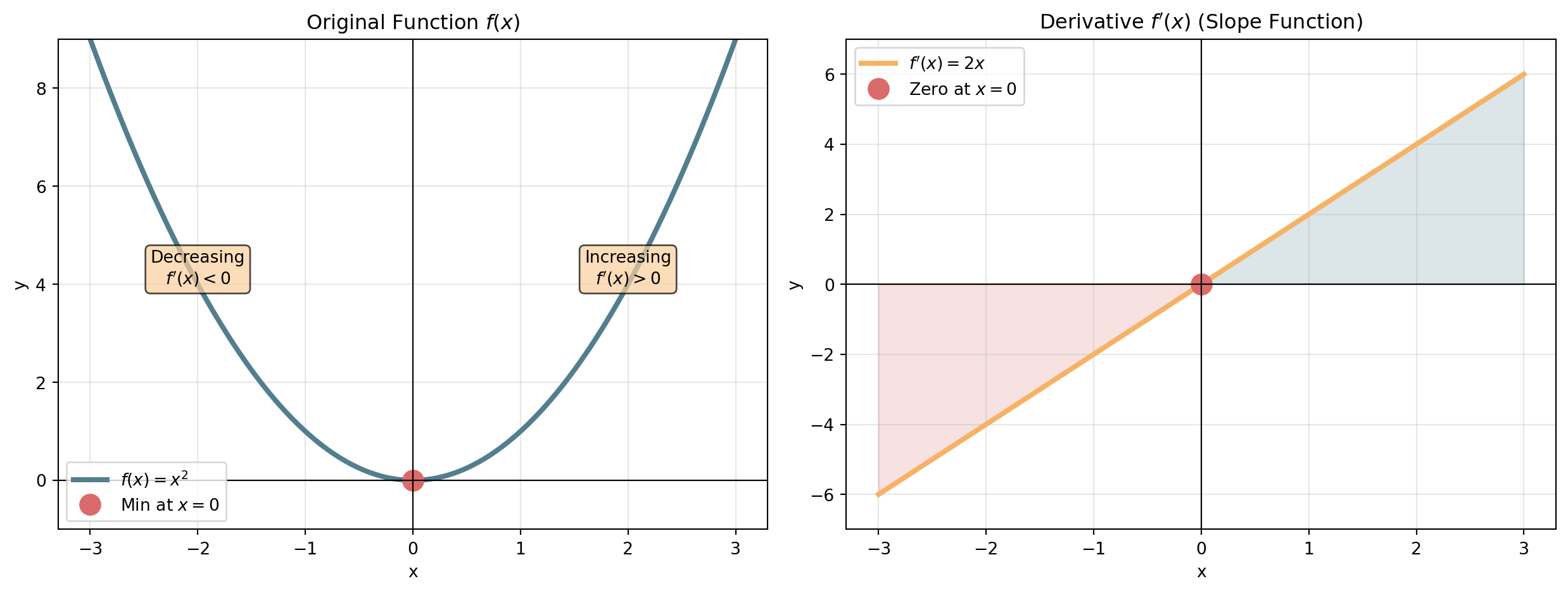
Sketching \(f'\) from \(f\)

A parabola and its derivative: \(f(x) = x^2\)

. . .

\(f\) has minimum at \(x = 0\) → \(f'\) crosses zero

Step-by-Step: Sketching the Derivative

The process is rather straightforward:

1. Identify critical points: Where does \(f\) have horizontal tangents? Mark these as zeros of \(f'\)

2. Determine sign: Where is \(f\) increasing/decreasing? Make \(f'\) positive/negative accordingly

3. Consider steepness:

   • Where is \(f\) very steep? Make \(|f'|\) large.
   • Where is \(f\) nearly flat? Make \(|f'|\) small.

4. Check concavity: Is \(f'\) increasing or decreasing? This tells you about the concavity of \(f\)

Complex Example

A cubic function and its derivative.

. . .

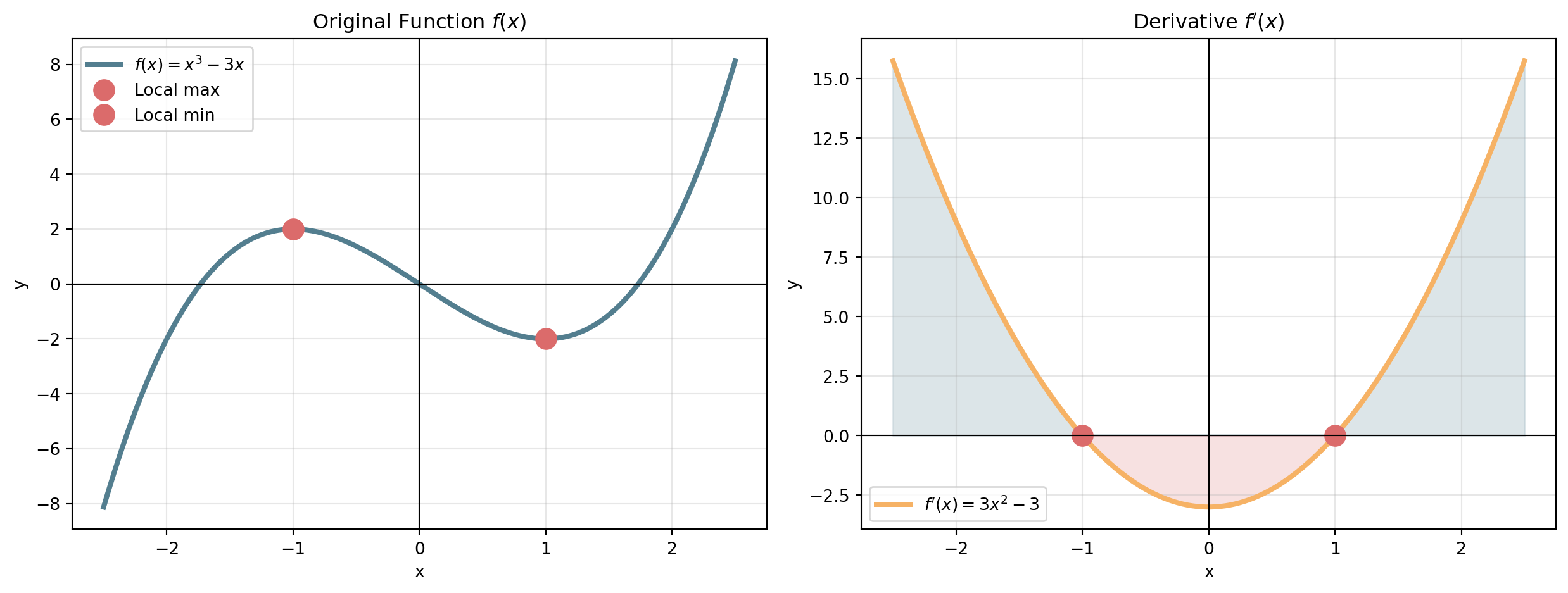
\(f\) increasing, then decreasing, then increasing → \(f'\) crosses zero twice

Critical Points

A point \(x = c\) where either:

• \(f'(c) = 0\) (horizontal tangent), or
• \(f'(c)\) does not exist (corner, cusp, vertical tangent)

. . .

TipClassification of Critical Points

• Local maximum: \(f'\) changes from positive to negative
• Local minimum: \(f'\) changes from negative to positive
  
• Neither: \(f'\) doesn’t change sign (e.g., \(f(x) = x^3\) at \(x = 0\))

Part B: From Derivative to Function

Reading Information from \(f'(x)\)

Given the graph of \(f'(x)\), we can determine:

1. Where \(f\) is increasing/decreasing:

   • \(f'(x) > 0\) → \(f\) is increasing
   • \(f'(x) < 0\) → \(f\) is decreasing

2. Where \(f\) has local extrema: \(f'\) crosses zero

   • Sign change determines type!

3. Where \(f\) is steepest: Where \(|f'(x)|\) is largest

4. Relative heights: Cannot determine absolute \(y\)-values!

   • Can determine relative changes!

Example: Reading from \(f'(x)\)

. . .

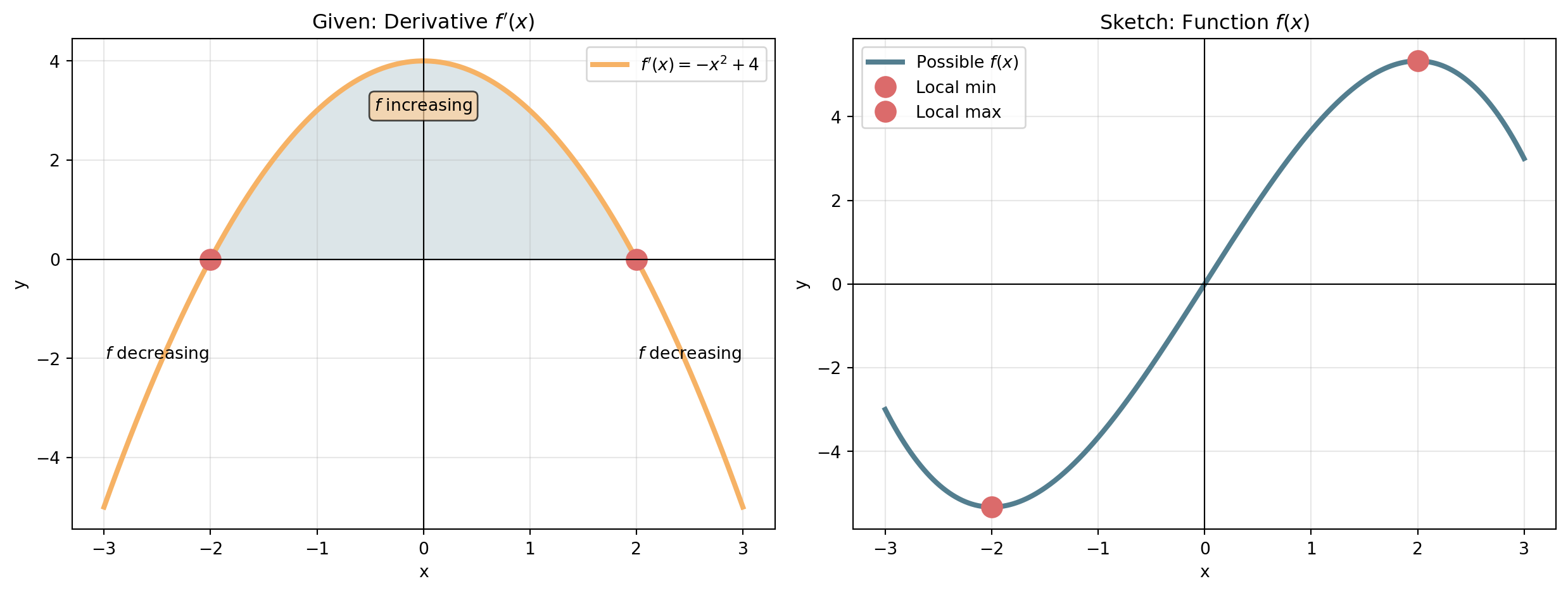
• \(f' > 0\) on \((-2, 2)\) → \(f\) increasing, \(f' < 0\) for \(|x| > 2\) → \(f\) decreasing
• \(f'\) changes at \(x = -2, 2\) → \(f\) has local extrema

Quick Practice - 10 Minutes

Individual Exercise I

Sketch the derivative of this function!

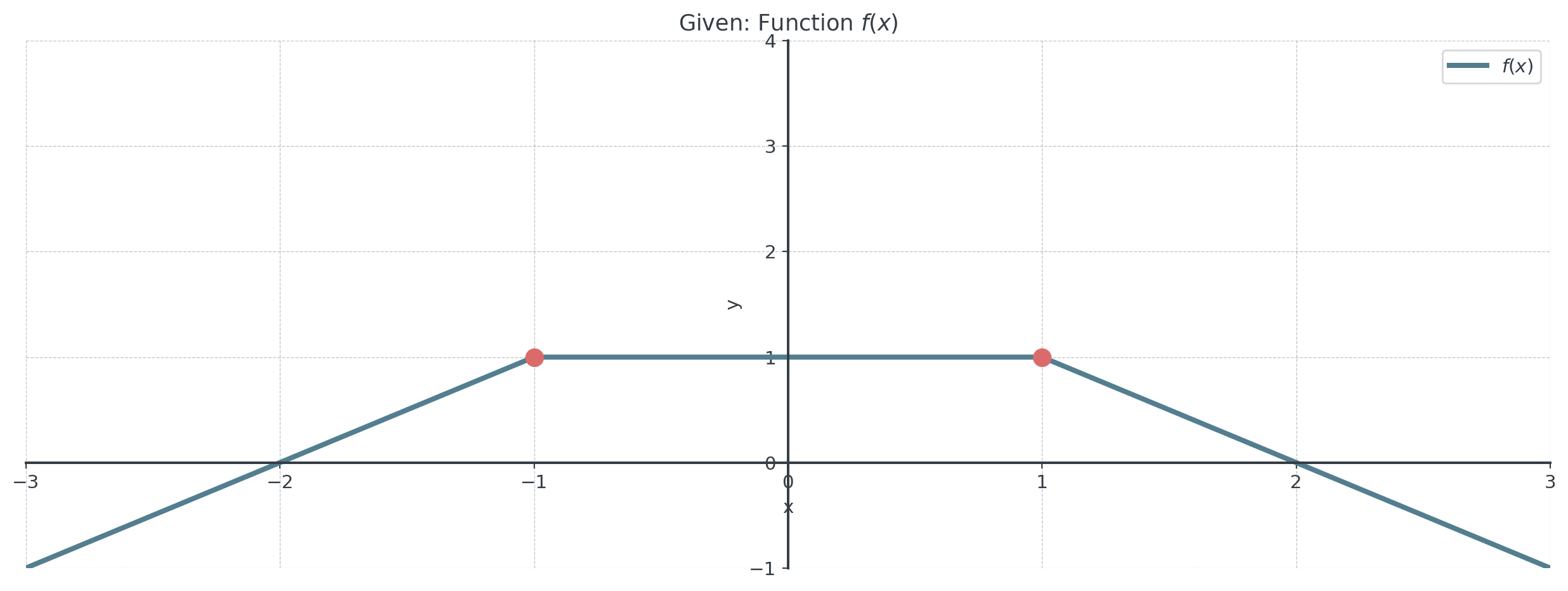
Individual Exercise II

The Questions:

1. Where is \(f'(x) > 0\), \(f'(x) < 0\), and \(f'(x) = 0\)?

2. Sketch the graph of \(f'(x)\).

3. At what points does \(f'(x)\) not exist?

Break - 10 Minutes

Part C: Second Derivatives and Concavity

Understanding Concavity

Describes the curving behavior of a function.

. . .

• Concave up (⌣): Curves upward like a smile
  • \(f''(x) > 0\)
  • The slope \(f'(x)\) is increasing
  • “Holds water”
• Concave down (⌢): Curves downward like a frown
  • \(f''(x) < 0\)
  • The slope \(f'(x)\) is decreasing
  • “Spills water”

Visualizing Concavity

Concave up vs. concave down

. . .

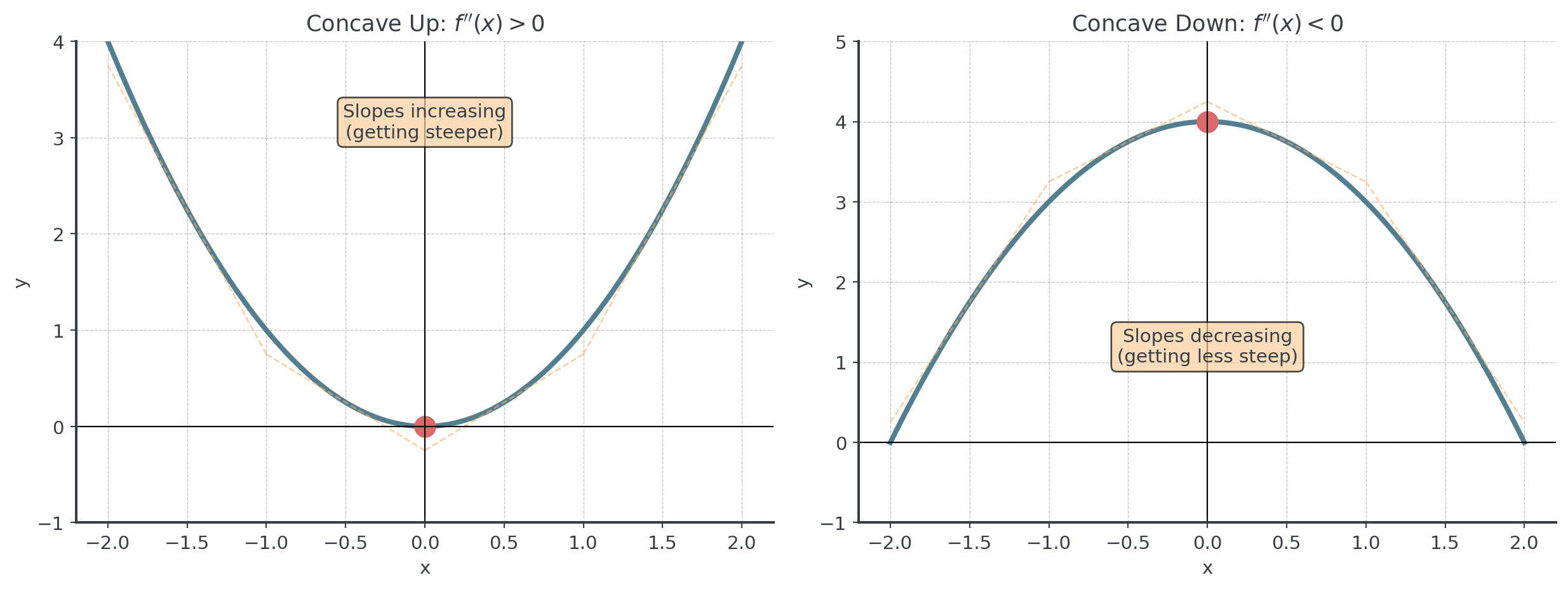
\(f''(x)\) tells us how \(f'(x)\) is changing, which determines the shape of \(f(x)\).

Inflection Points

A point where concavity changes!

. . .

• \(f''(x) = 0\) or \(f''(x)\) does not exist
• Concavity changes (from ⌣ to ⌢ or vice versa)

. . .

Example: \(f(x) = x^3\)

• \(f'(x) = 3x^2\)
• \(f''(x) = 6x\)
• \(f''(0) = 0\) and concavity changes at \(x = 0\)
• So \((0, 0)\) is an inflection point

Relationships Between \(f\), \(f'\), and \(f''\)

. . .

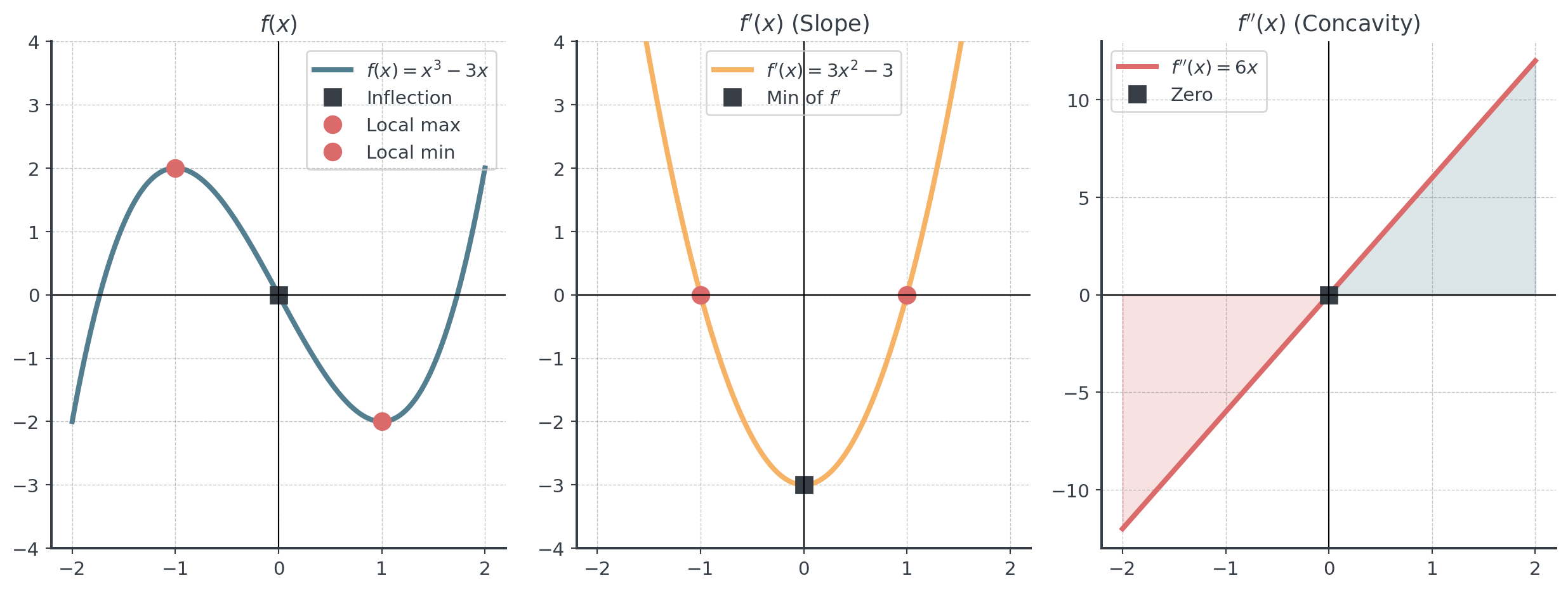
• Where \(f'' < 0\): \(f\) concave down, \(f'\) decreasing, where \(f'' > 0\): \(f\) concave up, \(f'\) increasing
• Where \(f'' = 0\): Inflection point in \(f\), extremum in \(f'\)

Part D: Complete Analysis

The Complete Picture

Given a function \(f(x)\), complete analysis involves:

1. Critical points: Solve \(f'(x) = 0\)
2. First derivative test: Check sign changes of \(f'\) to classify extrema
3. Inflection points: Solve \(f''(x) = 0\) and check for concavity change
4. Intervals: Determine where \(f\) is increasing/decreasing and where concave up/down
5. Key points: Evaluate \(f\) at critical points and inflection points

Example: Complete Analysis

Analyze \(f(x) = x^4 - 4x^3\)

. . .

First derivative:

. . .

\[f'(x) = 4x^3 - 12x^2 = 4x^2(x - 3)\]

. . .

Critical points: \(x = 0, 3\)

. . .

Second derivative:

. . .

\[f''(x) = 12x^2 - 24x = 12x(x - 2)\]

. . .

Inflection points: \(x = 0, 2\)

Analysis Visualization

Complete analysis of f(x) = x⁴ - 4x³

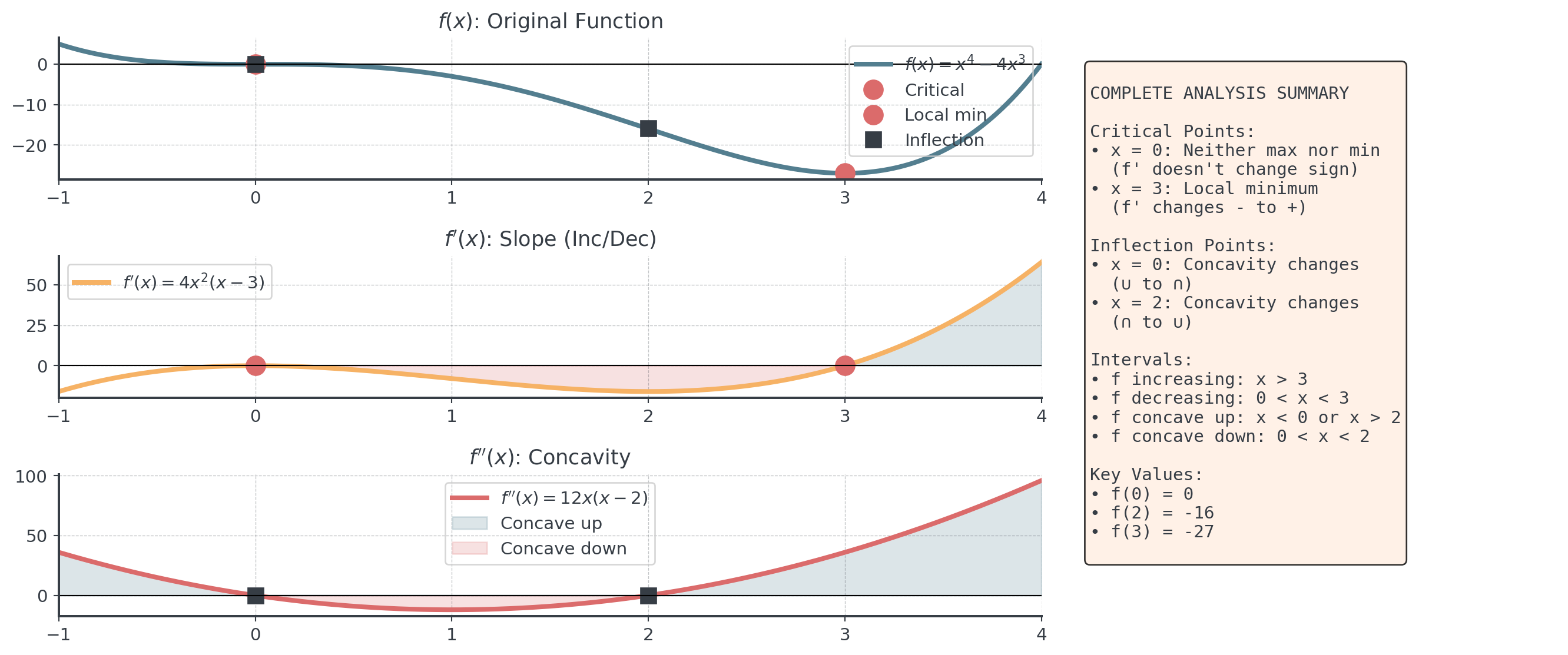
Guided Practice

Practice Set A: Sketching Derivatives

For each function graphed below, sketch \(f'(x)\) and identify:

• Where \(f'(x) > 0, < 0, = 0\) and any points where \(f'\) does not exist

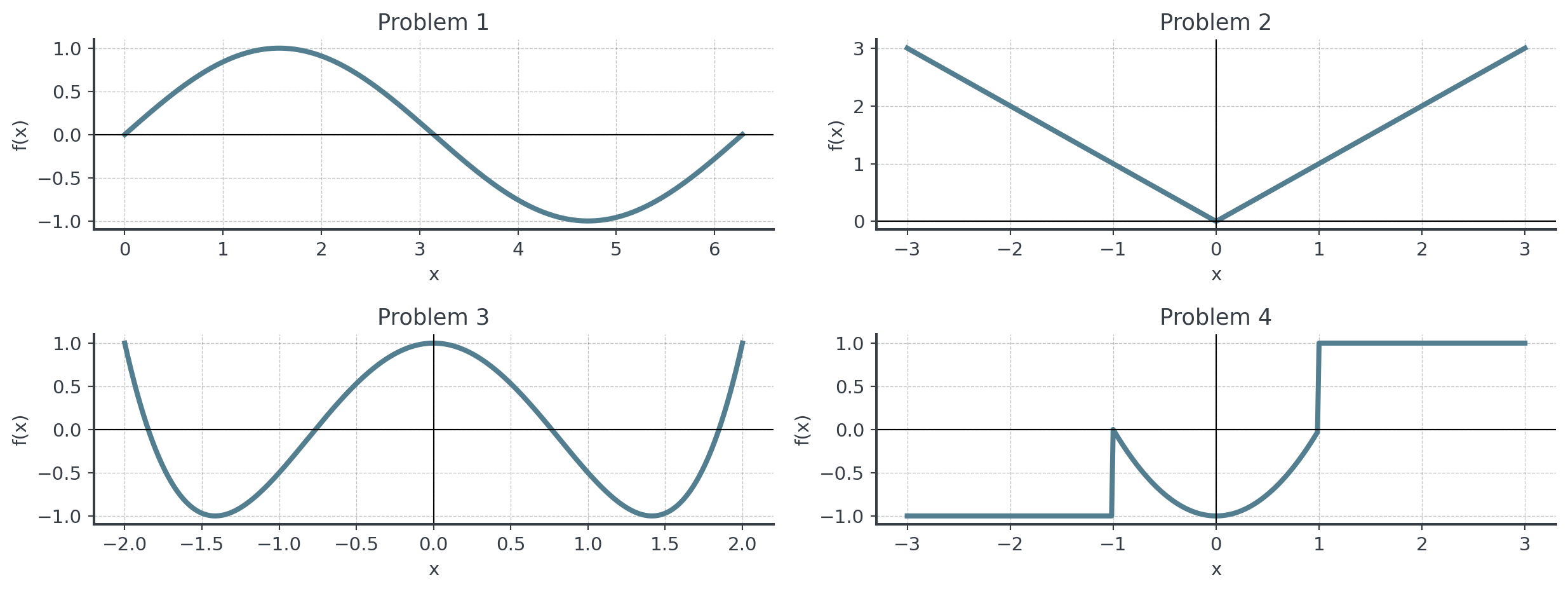
Practice B: From Derivative I

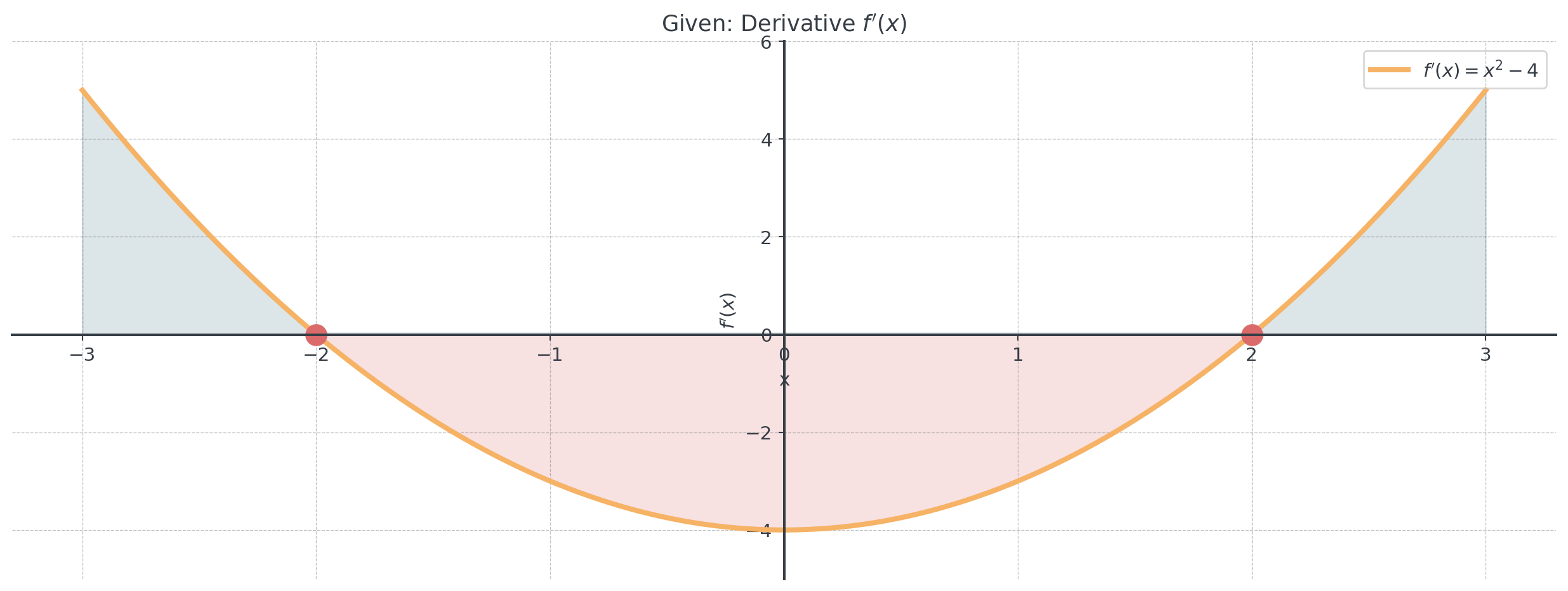
Continue working for 10 minutes

Given the graph of \(f'(x)\), answer:

1. Where is \(f(x)\) increasing/decreasing?
2. Where does \(f(x)\) have local extrema? Classify them.
3. Sketch a possible graph of \(f(x)\).

Practice B: From Derivative II

Quick Practice: Derivative Sketching

Work individually for 5 minutes

For each function described, sketch both \(f(x)\) and \(f'(x)\):

1. \(f(x) = x^3 - 3x\) (cubic with local max and min)

2. \(f(x) = |x - 2|\) (V-shape shifted right)

3. \(f(x)\) is constant for \(x < 0\), then increases linearly for \(x \geq 0\)

4. \(f(x)\) has \(f'(x) > 0\) everywhere but \(f'(x) \to 0\) as \(x \to \infty\)

Coffee Break - 15 Minutes

Business Applications

Profit Function Analysis

Business Context: A company’s monthly profit (in thousands €) is modeled by: \[P(t) = -t^3 + 12t^2 - 36t + 50\] where \(t\) is months since product launch.

. . .

Questions:

1. When is profit increasing/decreasing?
2. When does profit reach local extrema?
3. When is the rate of profit change accelerating/decelerating?

Profit Analysis Solution

First derivative (profit rate of change): \[P'(t) = -3t^2 + 24t - 36 = -3(t^2 - 8t + 12) = -3(t - 2)(t - 6)\]

. . .

Critical points: \(t = 2, 6\) months

. . .

Second derivative (acceleration of profit change): \[P''(t) = -6t + 24 = -6(t - 4)\]

. . .

Inflection point: \(t = 4\) months

Profit Visualization

. . .

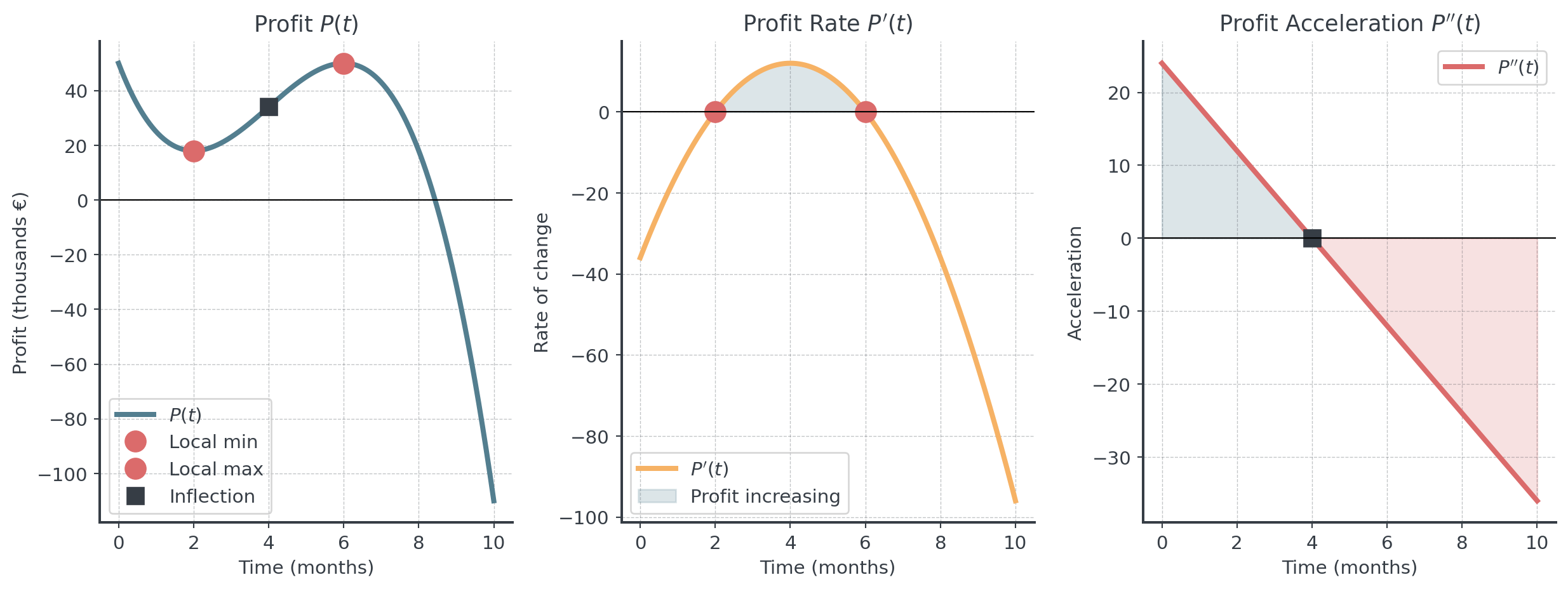
Question: How would you describe the behaviour?

Profit Interpretation

TipReading Business Graphs: Quick Rules

• \(P'(t) > 0\) → Profit is growing (good news!)
• \(P'(t) < 0\) → Profit is shrinking (warning sign)
• \(P'(t) = 0\) → Profit has reached a turning point (decision time)

The sign of the derivative tells you the direction of change!

. . .

NoteInflection Points in Business

The inflection point (\(P''(t) = 0\) at month 4) marks where:

• Before: Profit is accelerating (growth speeding up)
• After: Profit is decelerating (growth slowing down)

Business insight: Month 4 is when the company should start planning for the eventual peak. Growth is still positive but momentum is fading!

Collaborative Problem-Solving

Challenge: Complete Function Analysis

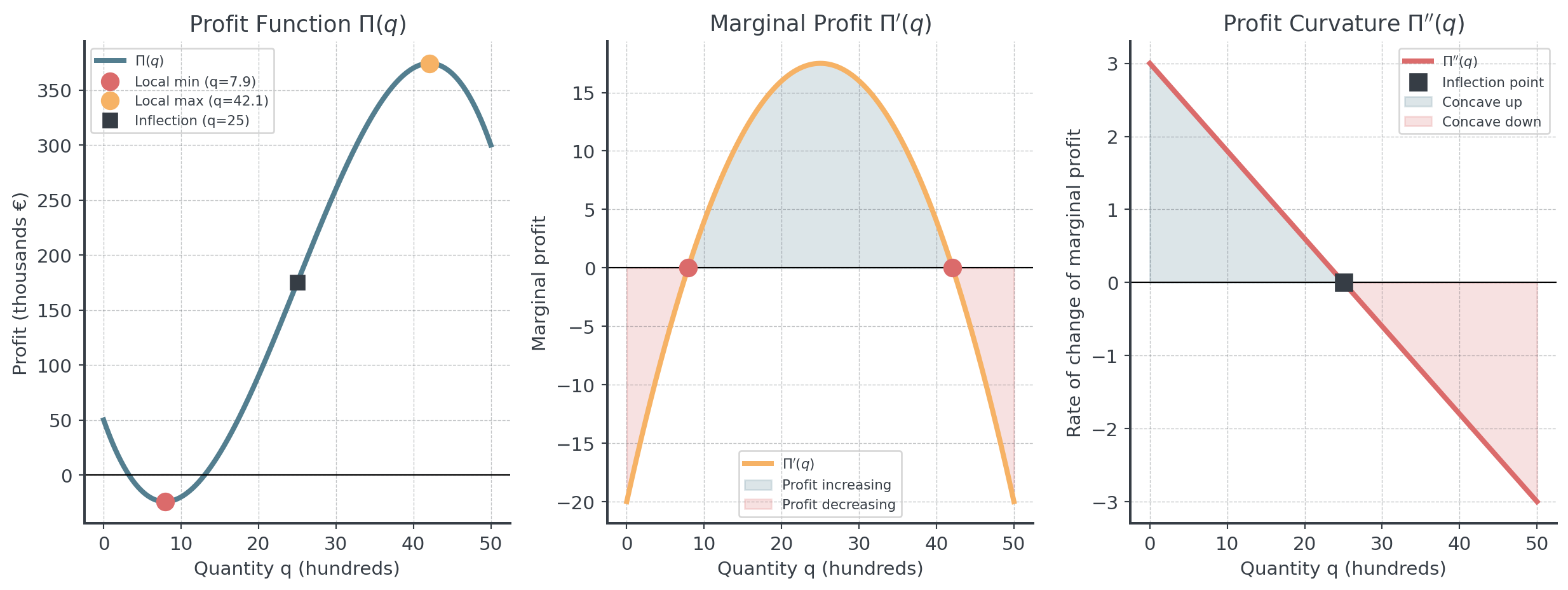
Scenario: A manufacturing company models their weekly profit (in thousands €) as a function of production quantity:

\[\Pi(q) = -0.02q^3 + 1.5q^2 - 20q + 50\]

where \(q\) is quantity produced (in hundreds of units), with \(q \in [0, 50]\).

Tasks

Work in groups of 3-4

1. Find \(\Pi'(q)\) and determine where profit is increasing vs. decreasing. Interpret economically.

2. Find \(\Pi''(q)\) and locate any inflection points - what do they say about profit growth?

3. Sketch the graphs of \(\Pi(q)\), \(\Pi'(q)\), and \(\Pi''(q)\) on \(q \in [0, 50]\).

4. Find all critical points and classify them as local maxima or minima using the second derivative test.

5. Business question: Current production is 1,500 units (\(q = 15\)) - raise or lower it, and by how much? Justify with calculus.

Think-Pair-Share - 7 Minutes

Discussion Question

Think individually, then discuss with class

Question: Consider these scenarios:

• Company A: Stock price \(S_A(t)\) is \(S'_A > 0\) but \(S''_A < 0\)
• Company B: Stock price \(S_B(t)\) is \(S'_B < 0\) but \(S''_B > 0\)

1. Which company is in a better position right now?
2. Which company shows more promising momentum for the future?
3. In financial terms, what do \(S'\) and \(S''\) represent?
4. Can you think of real-world examples of each scenario?

Wrap-Up & Key Takeaways

The Derivative Overview

If you know…	You can determine…
\(f' > 0\)	\(f\) is increasing
\(f' < 0\)	\(f\) is decreasing
\(f' = 0\)	Possible local extremum
\(f'' > 0\)	\(f\) concave up, \(f'\) increasing
\(f'' < 0\)	\(f\) concave down, \(f'\) decreasing
\(f'' = 0\)	Possible inflection point

. . .

These are heavily Tested Skills in FSP!!!

Final Assessment - 5 Minutes

Quick Check I

Consider this function:

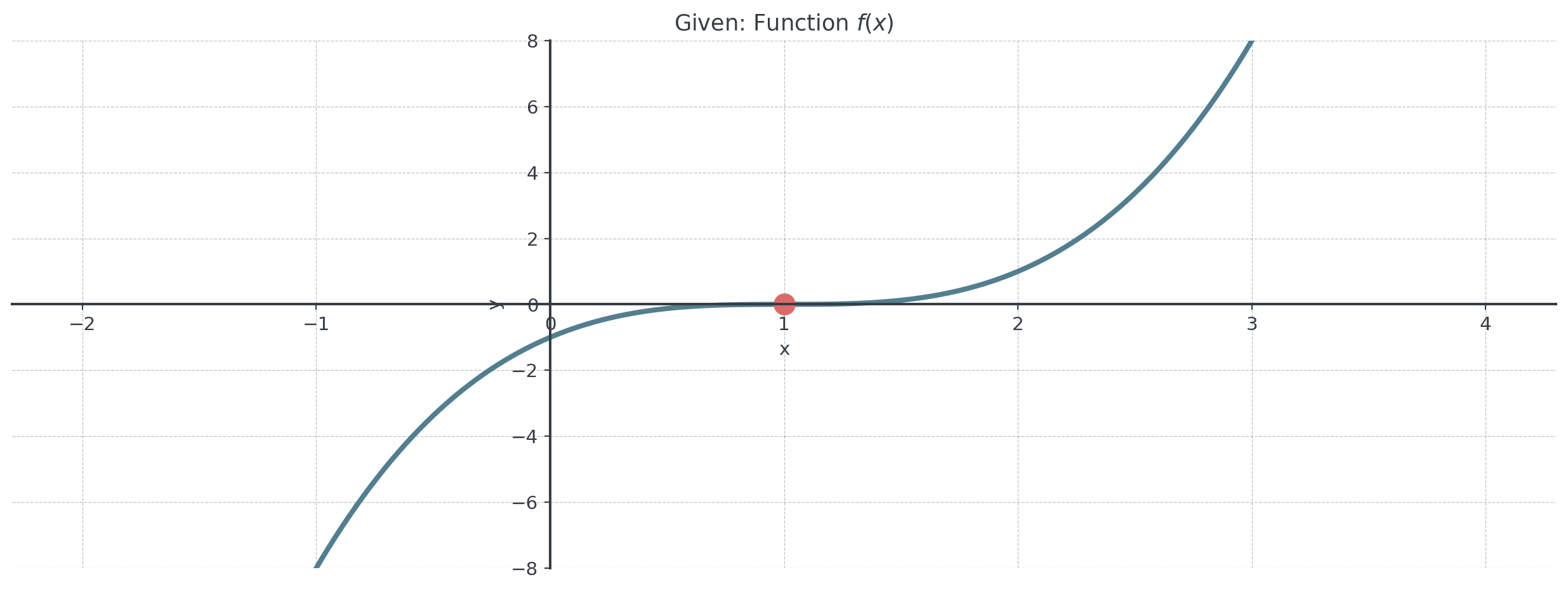
Quick Check II

Work individually, then we compare

1. Where is \(f'(x) > 0\)?

2. At \(x = 1\), is this a local max, local min, or neither?

3. Where is \(f(x)\) concave up?

4. True or False: If \(f'(c) = 0\), then \(f\) must have a local extremum at \(x = c\).

Next Session Preview

Session 05-06

Optimization & Curve Sketching

• First and second derivative tests for extrema classification
• Global maxima/minima on closed intervals
• Complete curve sketching algorithm (6 steps)
• Business optimization: profit maximization, cost minimization
• Interpreting results in real-world context

. . .

Complete Tasks 05-05!

Appendix

Profit function and its derivatives