Session 05-07 - Function Determination & Funktionsscharen

Section 05: Differential Calculus

Author

Dr. Nikolai Heinrichs & Dr. Tobias Vlćek

Entry Quiz - 10 Minutes

Quick Review from Session 05-06

Test your understanding of optimization and curve sketching

For \(f(x) = x^3 - 6x^2 + 9x\), find all critical points and classify them.
What is the difference between a local maximum and an absolute maximum?
Find the absolute extrema of \(g(x) = x^2 - 4x + 1\) on \([0, 3]\).
A profit function is \(P(x) = -2x^2 + 40x - 100\). What production level maximizes profit?

Homework Discussion - 15 Minutes

Your questions from Session 05-06

What questions do you have regarding the previous session?

Learning Objectives

What You’ll Master Today

Set up systems of equations from function conditions
Apply point conditions to determine unknown coefficients
Use tangent/slope conditions with derivatives
Incorporate extrema conditions (f’(a) = 0 and f(a) = b)
Master Funktionsscharen (function families with parameters)
Analyze how parameters affect zeros, extrema, and inflection points
Apply systematic problem-solving to business scenarios

. . .

Funktionsscharen are heavily tested on exams! Both function determination and Funktionsscharen share a key skill: setting up equations from conditions systematically.

Part A: Point Conditions and System Setup

The General Approach

Strategy for Finding Unknown Functions:

Choose the function form (polynomial degree, rational, etc.)
Count unknowns (how many coefficients?)
Identify conditions (points, slopes, extrema, etc.)
Set up equations from conditions
Solve the system
Verify the solution

. . .

Number of conditions = Number of unknowns

For a function with \(n\) unknowns, you need exactly \(n\) independent conditions!

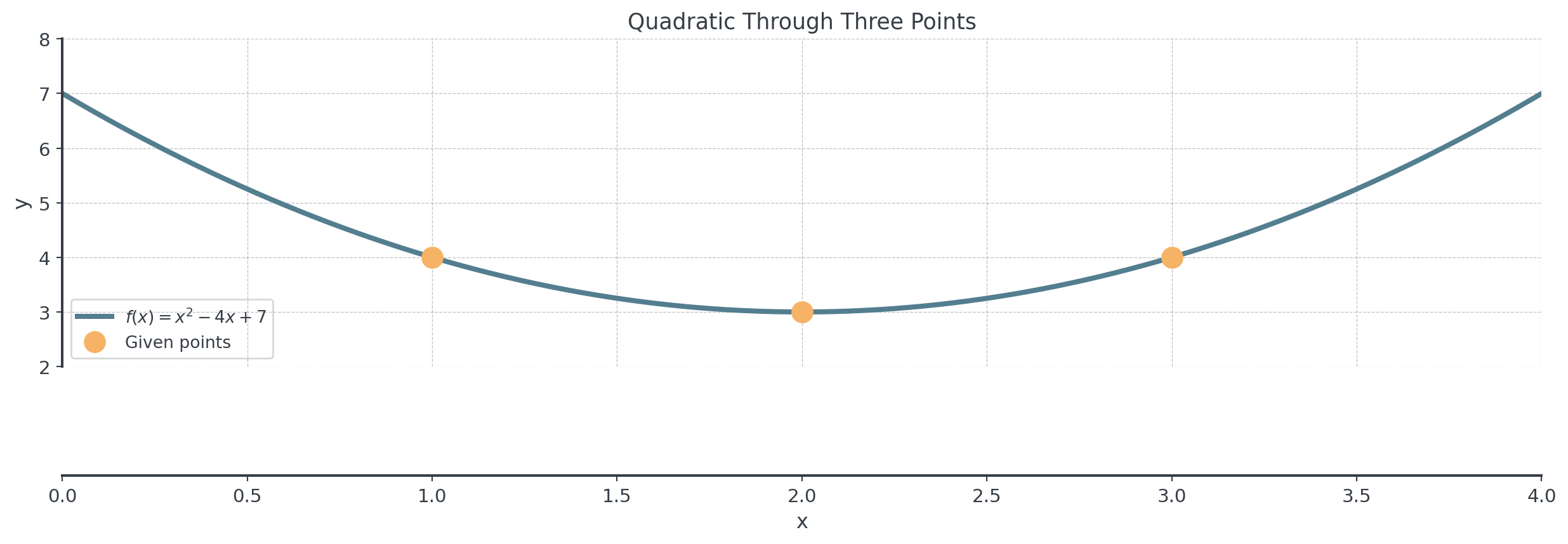
Example: Quadratic Three Points

Problem:

Find the quadratic function \(f(x) = ax^2 + bx + c\) passing through \((1, 4)\), \((2, 3)\), and \((3, 4)\).

. . .

Solution:

Function form: \(f(x) = ax^2 + bx + c\) (3 unknowns: \(a, b, c\))
Three point conditions (need 3 equations)
- \(f(1) = 4: \quad a(1)^2 + b(1) + c = 4 \quad \implies \quad a + b + c = 4\)
- \(f(2) = 3: \quad a(4) + b(2) + c = 3 \quad \implies \quad 4a + 2b + c = 3\)
- \(f(3) = 4: \quad a(9) + b(3) + c = 4 \quad \implies \quad 9a + 3b + c = 4\)

Solving the System

System of equations:

\(\begin{cases} a + b + c = 4 \\ 4a + 2b + c = 3 \\ 9a + 3b + c = 4 \end{cases}\)

. . .

Answer: \(f(x) = x^2 - 4x + 7\)

. . .

Check: Does \(f(x) = x^2 - 4x + 7\) pass through all three points?

. . .

\(f(1) = 1 - 4 + 7 = 4\) ✓
\(f(2) = 4 - 8 + 7 = 3\) ✓
\(f(3) = 9 - 12 + 7 = 4\) ✓

Visualizing the Solution

Part B: Tangent and Derivative Conditions

Using Derivative Conditions

Key Idea: Derivative conditions give us additional equations!

. . .

Common derivative conditions:

Slope at a point: \(f'(a) = m\)
- “The tangent line at \(x = a\) has slope \(m\)”
Horizontal tangent: \(f'(a) = 0\)
- “The function has a horizontal tangent at \(x = a\)”
Parallel tangents: \(f'(a) = f'(b)\)
- “Slopes at two points are equal”

. . .

Remember: Each derivative condition counts as one equation!

Example 2: Quadratic Point and Slope

Problem:

Find \(f(x) = ax^2 + bx + c\) such that:
- Passes through \((1, 3)\)
- Has slope \(2\) at \(x = 1\)
- Passes through \((2, 5)\)

. . .

Solution:

. . .

Step 1: \(f(x) = ax^2 + bx + c\) and \(f'(x) = 2ax + b\) (3 unknowns)

Solving with Derivative Conditions

Step 2: Set up equations from conditions:

Point \((1, 3)\): \(a + b + c = 3\)
Slope at \(x=1\): \(f'(1) = 2a + b = 2\)
Point \((2, 5)\): \(4a + 2b + c = 5\)

. . .

System: \(\begin{cases} a + b + c = 3 \\ 2a + b = 2 \\ 4a + 2b + c = 5 \end{cases}\)

. . .

Answer: \(f(x) = 2x + 1\) (actually linear, not quadratic!)

Part C: Extrema Conditions

Extrema Give TWO Conditions

Important: When a function has an extremum (max or min) at \((a, b)\):

. . .

You get TWO conditions:

Point condition: \(f(a) = b\) (the function passes through the point)
Horizontal tangent: \(f'(a) = 0\) (slope is zero at extremum)

. . .

Total: 2 equations from one extremum condition!

. . .

Don’t forget the \(f'(a) = 0\) condition!

An extremum at \((a, b)\) gives you both the point and the derivative condition.

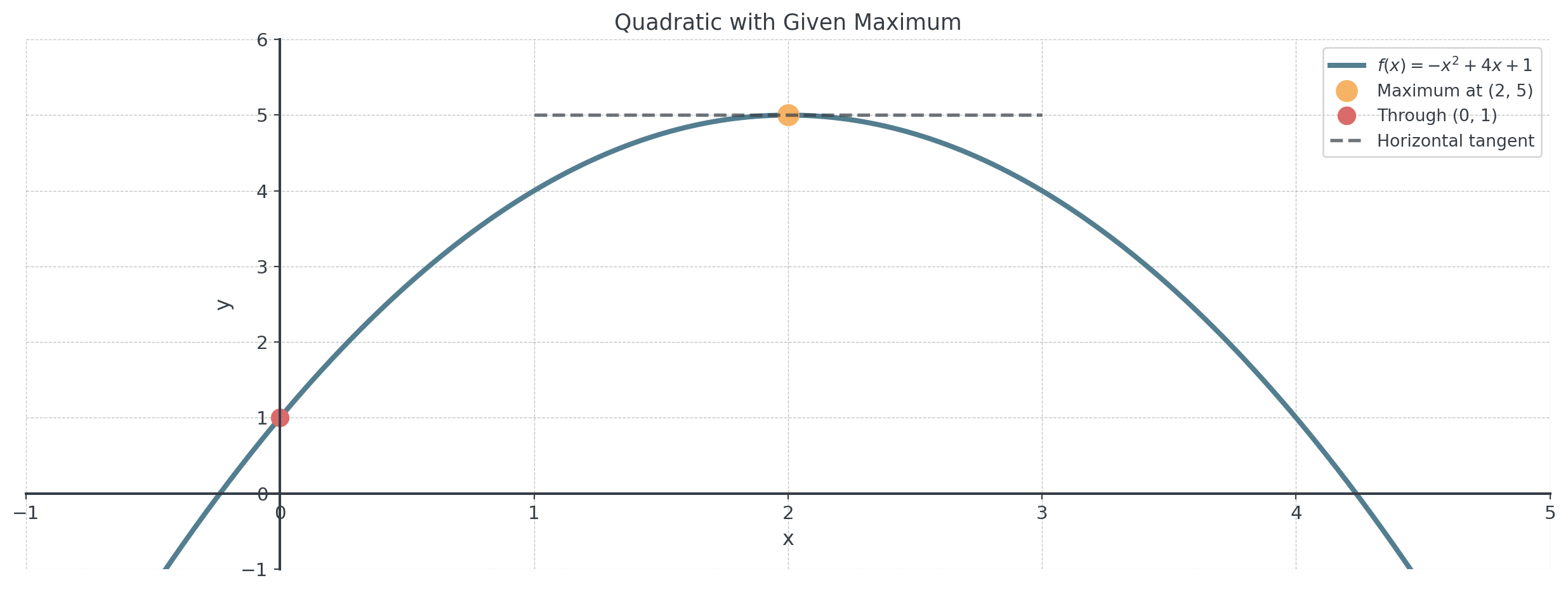
Example 3: Quadratic with Maximum

Problem: Find the quadratic function with a maximum at \((2, 5)\) that passes through \((0, 1)\).

. . .

Solution:

. . .

\(f(x) = ax^2 + bx + c\) (3 unknowns)

. . .

Conditions:

Point \((0, 1)\): \(f(0) = 1\)
Maximum at \((2, 5)\): \(f(2) = 5\)
Horizontal tangent at max: \(f'(2) = 0\)

Solving the Extremum System

Important: \(f'(x) = 2ax + b\)

. . .

Equations:

\(\begin{cases} c = 1 & \text{from } f(0) = 1 \\ 4a + 2b + c = 5 & \text{from } f(2) = 5 \\ 4a + b = 0 & \text{from } f'(2) = 0 \end{cases}\)

. . .

Answer: \(f(x) = -x^2 + 4x + 1\)

. . .

Verification: \(f''(x) = -2 < 0\) confirms maximum ✓

Visualizing the Maximum

Example 4: Parabola with Vertex Form

Problem: Find the parabola with vertex at \((3, -2)\) passing through \((1, 6)\).

. . .

Two approaches:

Approach 1 - Standard form: \(f(x) = ax^2 + bx + c\) (harder)
Approach 2 - Vertex: \(f(x) = a(x - h)^2 + k\) where \((h, k)\) vertex

. . .

Now it’s easy!

Using vertex form with \((h, k) = (3, -2)\):
\(f(x) = a(x - 3)^2 - 2\)
Only 1 unknown (\(a\)) now!

Vertex Simplification

Condition: Passes through \((1, 6)\):

\(f(1) = a(1 - 3)^2 - 2 = 6\)
\(4a - 2 = 6\)
\(a = 2\)

. . .

Answer:

\(f(x) = 2(x - 3)^2 - 2\)
Expanded: \(f(x) = 2x^2 - 12x + 16\)

Break - 10 Minutes

Part D: Mixed Conditions and Function Families

Multiple Conditions I

Strategy for Complex Problems:

List all unknowns clearly
Identify each condition type:
- Point: \(f(a) = b\)
- Slope: \(f'(a) = m\)
- Extremum: \(f(a) = b\) AND \(f'(a) = 0\)
- Inflection: \(f''(a) = 0\) (and possibly \(f(a) = b\))

. . .

Remember that the number of unknowns must match the number of conditions!

Multiple Conditions II

Strategy for Complex Problems:

Write derivative(s) before setting up equations
Organize your system (group similar types)
Solve systematically (substitution or elimination)
Verify your answer

. . .

Not too complicated, right?

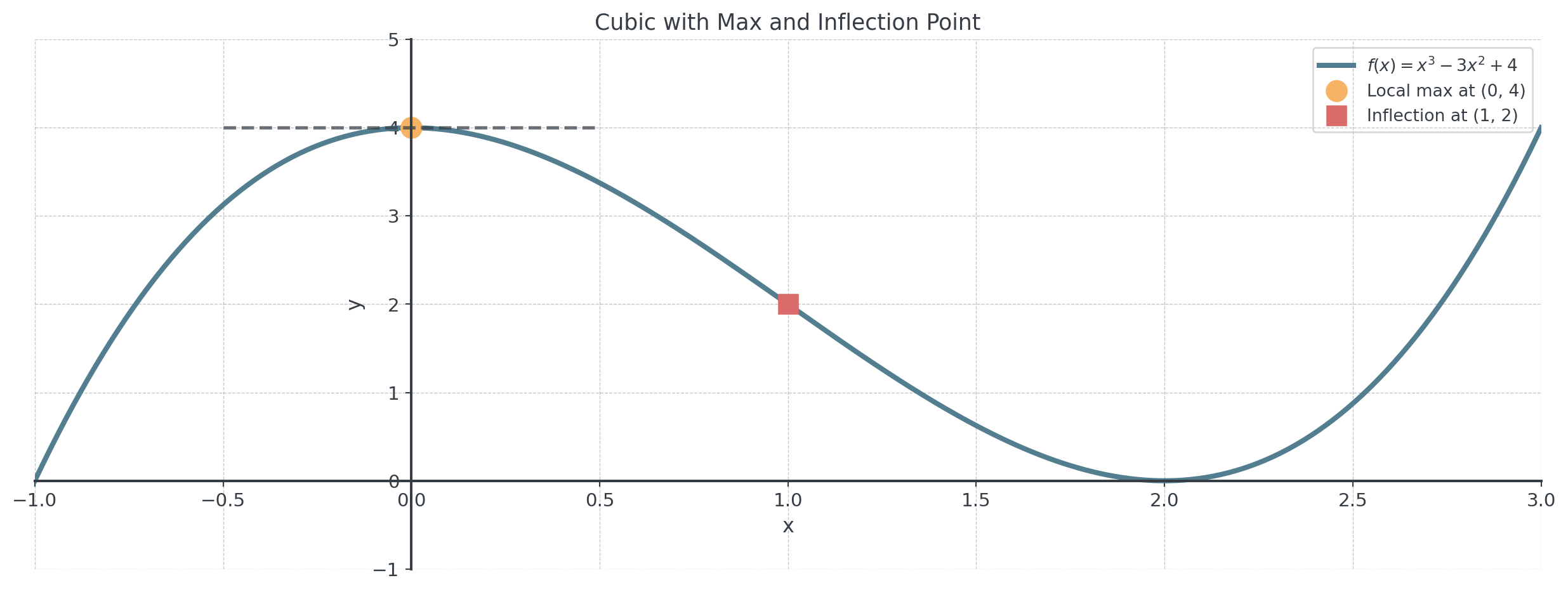
Example 5: Cubic Mixed Conditions

Problem: Find \(f(x) = ax^3 + bx^2 + cx + d\) such that:

Has a local maximum at \((0, 4)\)
Has an inflection point at \((1, 2)\)

. . .

Analysis: 4 unknowns, need 4 equations

Derivatives:
- \(f'(x) = 3ax^2 + 2bx + c\)
- \(f''(x) = 6ax + 2b\)

The Conditions

Now, remember the conditions we have:

\(f(0) = 4\): point condition
\(f'(0) = 0\): horizontal tangent at max
\(f(1) = 2\): point condition at inflection
\(f''(1) = 0\): inflection point condition

. . .

You will need to know these by heart in the exam!

Solving the Equations

Problem: Find \(f(x) = ax^3 + bx^2 + cx + d\) such that:

Has a local maximum at \((0, 4)\)
Has an inflection point at \((1, 2)\)

. . .

Equations:

\(f(0) = 4\): \(d = 4\)
\(f'(0) = 0\): \(c = 0\)
\(f(1) = 2\): \(a + b + c + d = 2\), so \(a + b = -2\)
\(f''(1) = 0\): \(6a + 2b = 0\), so \(3a + b = 0\)

Verification

Answer: \(f(x) = x^3 - 3x^2 + 4\)

. . .

Check all conditions for \(f(x) = x^3 - 3x^2 + 4\):

\(f(0) = 4\) ✓
\(f'(x) = 3x^2 - 6x\), so \(f'(0) = 0\) ✓
\(f(1) = 1 - 3 + 4 = 2\) ✓
\(f''(x) = 6x - 6\), so \(f''(1) = 0\) ✓

. . .

Additional check: \(f''(0) = -6 < 0\), confirming local maximum ✓

Visualizing Mixed Conditions

Part E: Funktionsscharen (Function Families)

Introduction to Funktionsscharen

Definition: A Funktionenschar is a family of functions that depend on a parameter we can vary (usually \(t\), \(a\), or \(k\)).

Notation: \(f_t(x)\) or \(f(x, t)\)
Example: \(f_t(x) = x^2 - tx + 1\)
- When \(t = 0\): \(f_0(x) = x^2 + 1\)
- When \(t = 2\): \(f_2(x) = x^2 - 2x + 1 = (x-1)^2\)
- When \(t = 4\): \(f_4(x) = x^2 - 4x + 1\)
Each value of \(t\) gives a different parabola!

Visualizing a Function Family

. . .

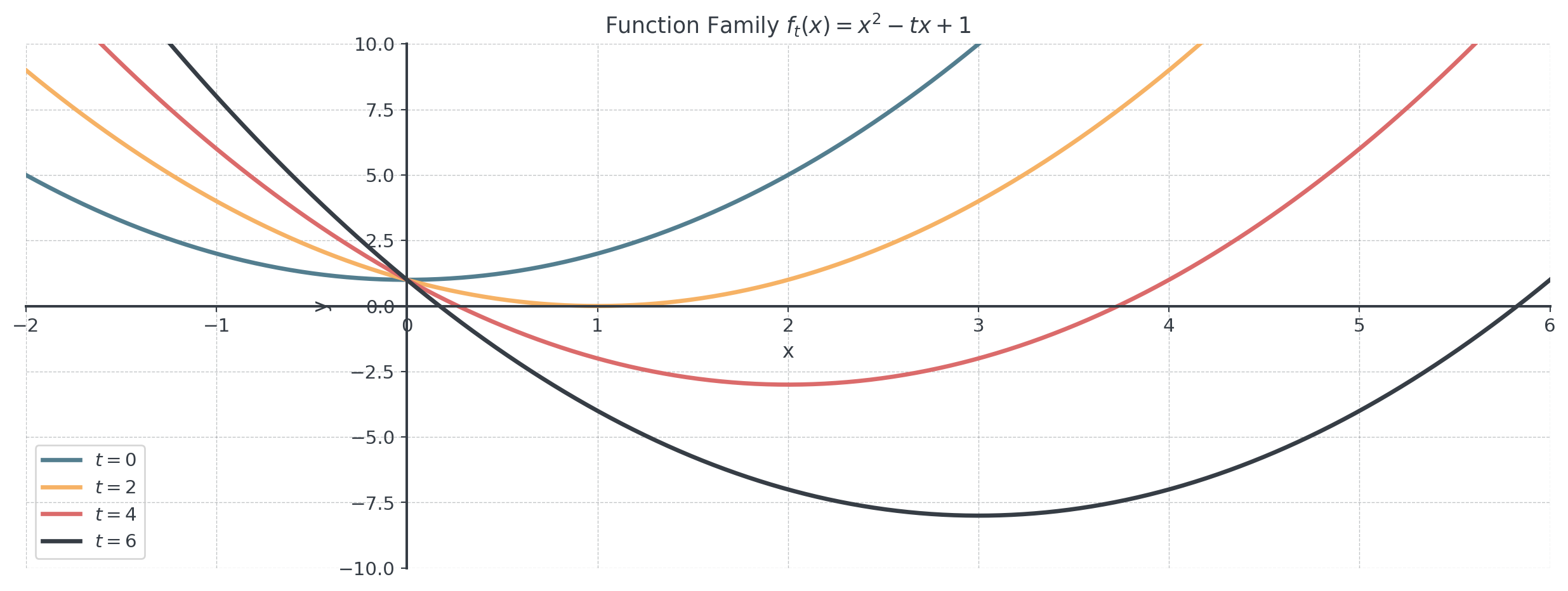
Its a collection of functions that are related to each other by a parameter.

Why Study Funktionsscharen?

Heavily tested on exams! Common question types:

For which \(t\) does \(f_t(x)\) have exactly 2 zeros?
For which \(t\) does \(f_t(x)\) have a local maximum at \(x = 3\)?
For which \(t\) is \(f_t(2) = 5\)?
Find the parameter \(t\) such that the inflection point is at \(x = 1\).

. . .

Practice these on your own as well, as we are coming to the end of this section!

Example

Problem: For which \(t\) does \(f_t(x) = x^2 - tx + t\) have exactly one zero?

. . .

Solution: Exactly one zero when the discriminant equals zero.
For \(x^2 - tx + t = 0\):
- \(\Delta = b^2 - 4ac = (-t)^2 - 4(1)(t) = t^2 - 4t\)
Set \(\Delta = 0\):
- \(t^2 - 4t = 0\)
- \(t(t - 4) = 0\)
- \(t = 0 \text{ or } t = 4\)
Answer: For \(t = 0\) or \(t = 4\), the function has exactly one zero.

General Strategy for Funktionsscharen

Identify condition: zeros, extrema, inflection points, function values
Set up the equation:
- Zeros: Use discriminant or factor
- Extrema: \(f_t'(x) = 0\)
- Inflection: \(f_t''(x) = 0\)
- Function value: \(f_t(a) = c\)
Substitute the given point (if specified)
Solve for the parameter \(t\)
Verify your answer makes sense

Guided Practice - 15 Minutes

Set A - Work in Pairs

Complete these problemsand then we discuss

Find the quadratic passing through \((1, 0)\), \((2, 3)\), and \((3, 8)\).
Find the cubic \(f(x) = ax^3 + bx^2 + cx + d\) with \(f(0) = 2\), \(f(1) = 3\), \(f'(0) = 1\), and \(f'(1) = 4\).
Find the parabola with vertex at \((2, -1)\) passing through \((0, 7)\).
For \(h_t(x) = x^2 - tx + 3\), find \(t\) such that \(h_t(2) = 5\).

Set B - Funktionsscharen Practice

Work individually for 10 minutes, then compare

For each Funktionschar, solve the given problem:

For \(f_t(x) = x^2 - 2tx + 3\), find all \(t\) such that \(f_t\) has exactly two zeros.
For \(g_t(x) = tx^2 - 4x + t\), find \(t\) such that \(g_t\) has a zero at \(x = 2\).
For \(h_t(x) = x^3 - tx^2 + 3x\), find \(t\) such that \(h_t\) has a local extremum at \(x = 1\).
For \(p_t(x) = x^2 + tx - 2t\), find \(t\) such that \(p_t(3) = 10\).
For \(q_t(x) = tx^2 - 6x + 9\), for which \(t\) does \(q_t\) have exactly one zero?

Coffee Break - 15 Minutes

Business Applications

Cost Function from Marginal Cost

Scenario: A company knows its marginal cost is:

\[MC(x) = C'(x) = 3x^2 - 12x + 20\]

The fixed cost (when \(x = 0\)) is €500.

. . .

Question: Find the total cost function \(C(x)\).

. . .

Solution: We need to find \(C(x)\) such that \(C'(x) = 3x^2 - 12x + 20\).

Integration

Integration (reverse of differentiation):

. . .

\[C(x) = x^3 - 6x^2 + 20x + k\]

where \(k\) is a constant.

. . .

Use the fixed cost condition \(C(0) = 500\):

. . .

\[C(0) = 0 - 0 + 0 + k = 500\]

. . .

\[k = 500\]

. . .

Answer: \(C(x) = x^3 - 6x^2 + 20x + 500\)

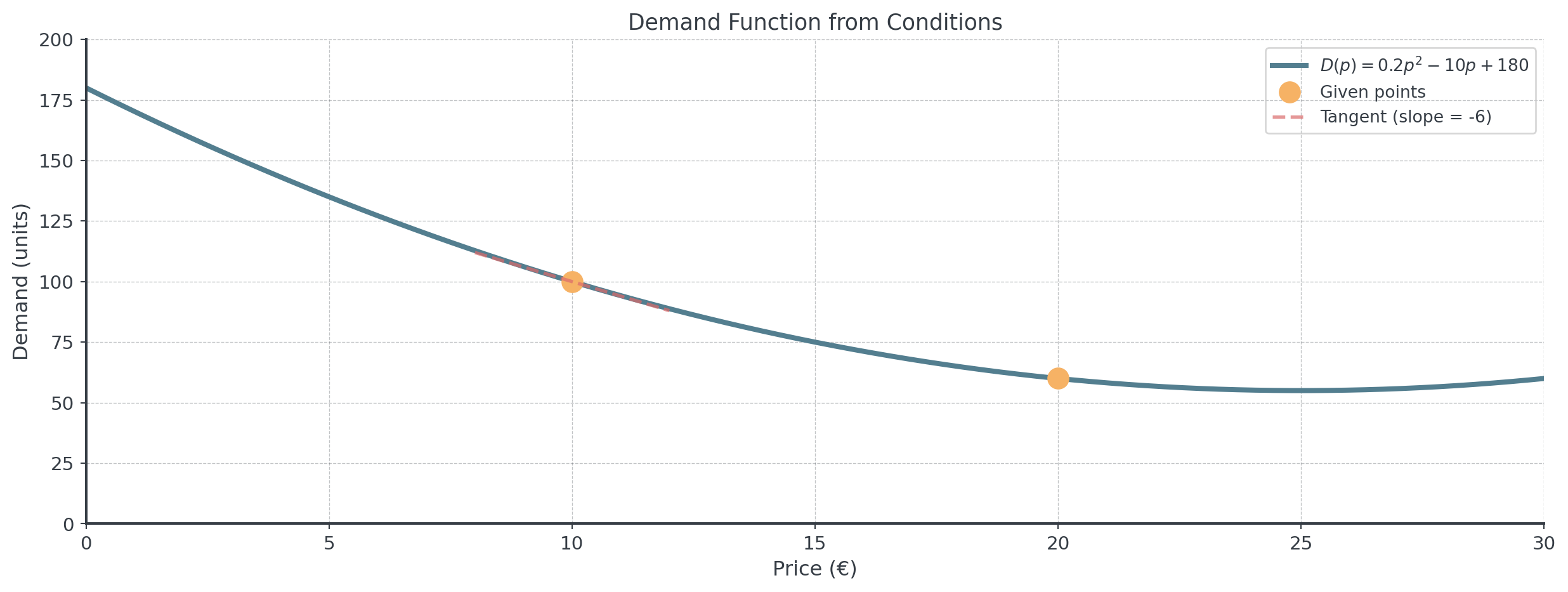
Demand Function Determination

Scenario: A product’s demand function is quadratic: \(D(p) = ap^2 + bp + c\) where \(p\) is price.

. . .

Known information:

At price €10, demand is 100 units: \(D(10) = 100\)
At price €20, demand is 60 units: \(D(20) = 60\)
The rate of change of demand at \(p = 10\) is \(-6\) units/euro
- \(D'(10) = -6\)

. . .

Question: Find the demand function.

Solving the Demand System

\(D'(p) = 2ap + b\)

. . .

System: \[\begin{cases} 100a + 10b + c = 100 \\ 400a + 20b + c = 60 \\ 20a + b = -6 \end{cases}\]

. . .

Answer: \(D(p) = 0.2p^2 - 10p + 180\)

Visualizing the Demand Function

Demand function D(p) = 0.2p² - 10p + 180

Collaborative Problem-Solving - 20 Minutes

Group Challenge I

Scenario:

An engineer is designing a roller coaster section modeled by a cubic function \(h(x) = ax^3 + bx^2 + cx + d\), where \(h\) is height (meters) and \(x\) is horizontal distance (meters).

Design requirements:

Starts at ground level: \(h(0) = 0\)
Reaches a peak (maximum) of 20 meters at \(x = 4\)
Returns to ground level at \(x = 10\): \(h(10) = 0\)

Group Challenge II

Work in groups of 3-4 students

How many unknowns and conditions do you have?
Set up the complete system of equations.
Solve for the coefficients \(a, b, c, d\).
Verify that \(x = 4\) is indeed a maximum (not minimum).
Find the height at \(x = 2\) and \(x = 8\).
Sketch the roller coaster section.

Wrap-Up & Key Takeaways

Summary of Session 05-07

Function Determination - Systematic Approach:

Count unknowns = count conditions needed
Write derivatives before setting up equations
Organize conditions by type: point, slope, extremum, inflection

. . .

Funktionsscharen - Parameter Analysis:

Identify the parameter (usually \(t\), \(a\), or \(k\))
Set up condition equations involving the parameter
Solve for parameter values meeting given criteria

Final Assessment - 5 Minutes

Quick Check

Complete individually and then discuss

How many conditions do you need to find a cubic function? How many does an extremum at \((a, b)\) provide?
Find the parabola with vertex at \((1, 4)\) passing through \((0, 2)\).
For \(f_t(x) = x^2 - 2tx + t\), find \(t\) such that \(f_t(x)\) has exactly one zero.
Find the quadratic \(g(x) = ax^2 + bx + c\) with \(g(0) = 3\), \(g(1) = 2\), and \(g'(1) = -4\).

Next Session Preview

Looking Ahead: Session 05-08

Topic: First Complete Assessment (Full Mock Exam)

180-minute mock exam under exam conditions
3 complete multi-part problems
Coverage: All differential calculus topics
Exact exam conditions, no assistance
Review of solutions after completion
Bring calculator

. . .

Get a good night’s sleep!

Thank You!

See you next session!