Tasks 05-01 - Limits & Continuity Through Graphs
Section 05: Differential Calculus
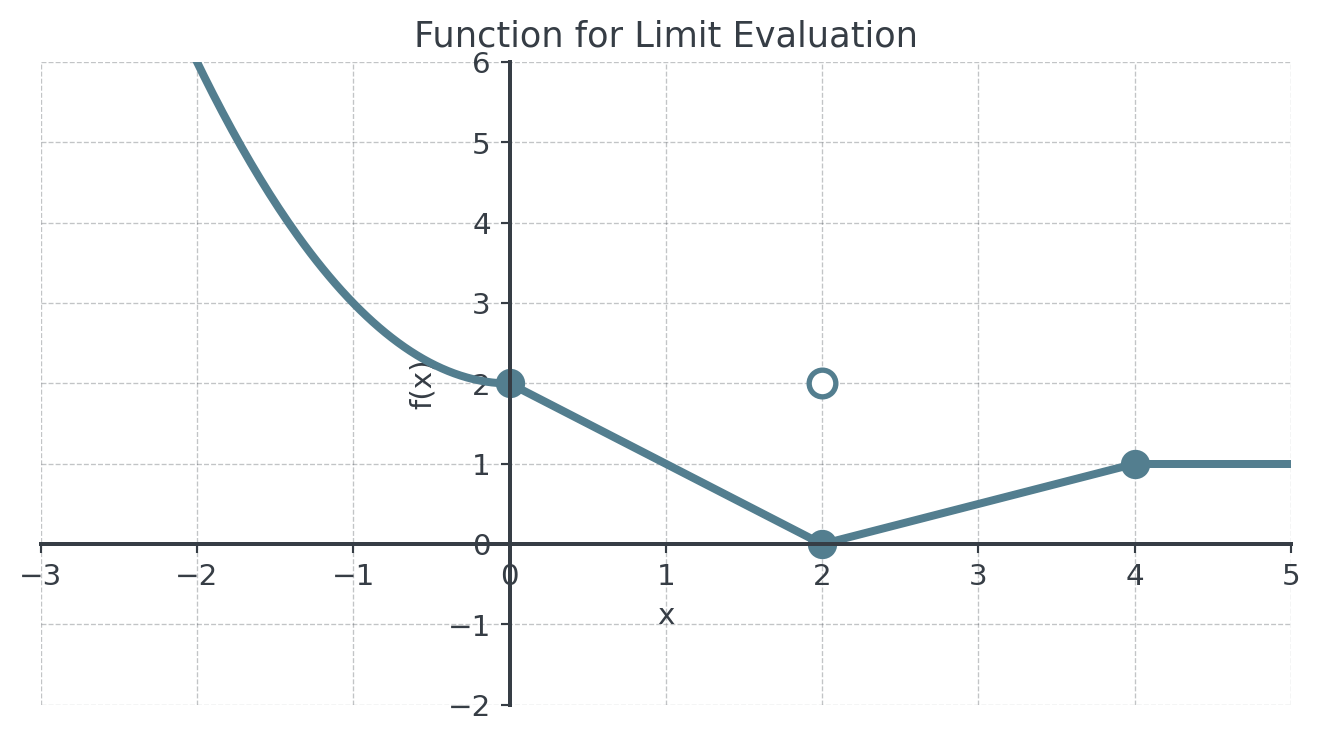
Problem 1: Basic Limit Evaluation (x)
Given the graph below, evaluate the following limits:
Determine \(\lim_{x \to 0} f(x)\)
Compute \(\lim_{x \to 2^-} f(x)\) and \(\lim_{x \to 2^+} f(x)\)
Verify whether \(\lim_{x \to 2} f(x)\) exists. If it does, give its value.
Explain why \(\lim_{x \to 4} f(x) = 1\)
Problem 2: One-Sided Limits and Discontinuities (x)
A company’s discount policy is given by the following function, where \(D(x)\) represents the discount percentage for an order of \(x\) units:
\[D(x) = \begin{cases} 0 & \text{if } 0 < x < 50 \\ 5 & \text{if } x = 50 \\ 10 & \text{if } 50 < x < 100 \\ 15 & \text{if } x \geq 100 \end{cases}\]
Determine \(\lim_{x \to 50^-} D(x)\) and \(\lim_{x \to 50^+} D(x)\)
Compute \(\lim_{x \to 100^-} D(x)\) and \(\lim_{x \to 100^+} D(x)\)
Verify whether the discount function is continuous at \(x = 50\) and \(x = 100\)
Sketch the graph of \(D(x)\) for \(0 < x < 150\)
Problem 3: Tax Bracket Analysis (xx)
A progressive tax system has the following marginal tax rates:
| Income Range | Marginal Tax Rate |
|---|---|
| €0 - €20,000 | 0% |
| €20,001 - €50,000 | 20% |
| €50,001 - €100,000 | 30% |
| Above €100,000 | 40% |
The tax owed function \(T(x)\) for income \(x\) is:
\[T(x) = \begin{cases} 0 & \text{if } 0 \leq x \leq 20000 \\ 0.2(x - 20000) & \text{if } 20000 < x \leq 50000 \\ 6000 + 0.3(x - 50000) & \text{if } 50000 < x \leq 100000 \\ 21000 + 0.4(x - 100000) & \text{if } x > 100000 \end{cases}\]
Investigate the continuity of \(T(x)\) at the bracket boundaries: €20,000, €50,000, and €100,000.
Compute the effective tax rate \(E(x) = \frac{T(x)}{x}\) for incomes of €19,999, €20,001, €49,999, and €50,001.
Argue why it’s important that \(T(x)\) is continuous while the marginal rate function is not.
Graph both \(T(x)\) and the marginal tax rate function for \(0 \leq x \leq 150000\).
Problem 4: Business Application - Production Cost Model (xx)
A manufacturer has different production methods available depending on quantity:
- Hand-crafted (0-50 units): \(C_1(x) = 100x + 200\)
- Semi-automated (50-200 units): \(C_2(x) = 40x + 3200\)
- Fully automated (200+ units): \(C_3(x) = 25x + 6200\)
The actual cost function includes a one-time setup cost of €500 when switching methods.
Determine the complete cost function \(C(x)\) including setup costs at transition points.
Calculate all limits at the transition points \(x = 50\) and \(x = 200\).
Assess whether it’s ever beneficial to produce exactly 50 or 200 units.
Decide on the optimal production quantity if demand is estimated between 180 and 220 units. Substantiate your recommendation.
Problem 5: Rational Function Analysis (xxx)
Consider the rational function: \[f(x) = \frac{x^3 - 8}{x^2 - 4}\]
Show that this function can be simplified and identify any holes.
Investigate the behavior of \(f(x)\) as \(x\) approaches 2 and -2. Determine all relevant limits.
Verify whether \(f\) can be made continuous by redefining it at certain points. If so, give the continuous extension.
Sketch the complete graph of \(f\), clearly marking all discontinuities, asymptotes, and key features.
Interpret this function as a cost model where discontinuities represent equipment failures. Explain the economic implications.
Problem 6: Complex Production Optimization (xxx)
A tech company manufactures smart home devices with a complex cost structure that depends on production volume and quality level. The cost function is:
\[C(x, q) = \begin{cases} 1000 + 50x + 10qx & \text{if } 0 < x < 100 \text{ (Prototype phase)} \\ 5000 + 30x + 8qx & \text{if } 100 \leq x < 500 \text{ (Small batch)} \\ 8000 + 25x + 5qx & \text{if } x \geq 500 \text{ (Mass production)} \end{cases}\]
where \(x\) is the number of units and \(q\) is the quality level (1 ≤ q ≤ 5).
The revenue function is \(R(x, q) = x \cdot (80 + 20q)\) (higher quality commands higher prices).
Part A: Continuity Analysis
Investigate whether the cost function is continuous at the transition points x = 100 and x = 500 for a fixed quality level q = 3.
Determine all quality levels \(q\) for which the cost function is continuous at x = 100.
Part B: Profit Optimization
Calculate the profit function \(P(x, q) = R(x, q) - C(x, q)\) for each production phase when q = 3.
Decide which production level maximizes profit if the company can produce between 450 and 550 units. Consider the transition at x = 500.
Graph the profit function for q = 3 over the range 0 < x < 700 and mark all discontinuities.
Argue whether the company should implement a continuous cost structure. What are the trade-offs?
