Rational & Logarithmic Functions

Session 04-05: Advanced Function Analysis

Author

Mathematics for Business Students

Entry Quiz - 10 Minutes

Review from Session 04-04

Work individually for 5 minutes, then we discuss

Transformations: If $g(x) = 2f(x-3) + 1$, describe all transformations from $f(x)$.
Logarithms: Simplify $\log_2(8x)$ using logarithm properties.
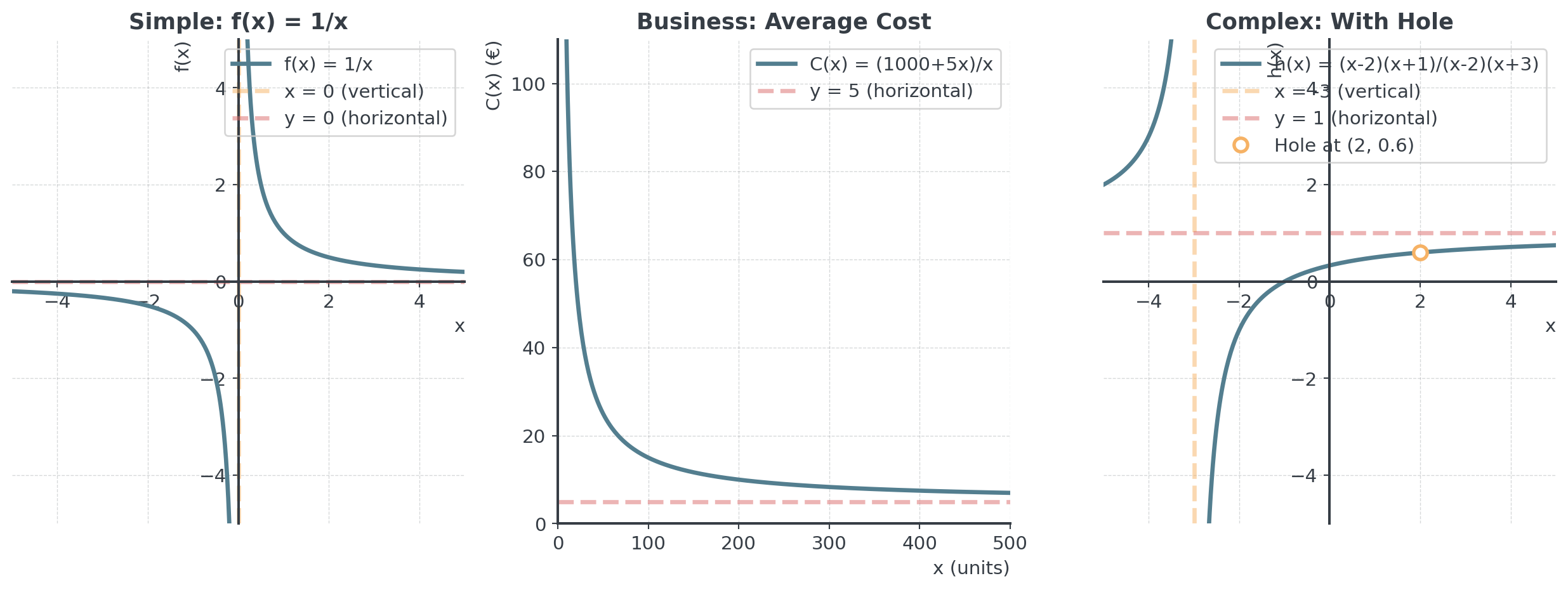
Rational Behavior: What happens to $\frac{1}{x}$ as $x \to 0^+$? As $x \to 0^-$?
Exponential Equation: Solve $2^{x-1} = 16$.

Homework Discussion - 15 Minutes

Your Questions from Tasks 04-04

Let’s discuss the problems you found challenging

Learning Objectives

Today’s Goals

By the end of this session, you will be able to:

Analyze rational functions completely (asymptotes, holes, intercepts)
Understand logarithmic properties and transformations
Master semi-log and log-log scales
Model business scenarios with average cost functions
Interpret exponential growth using logarithmic scales
Solve complex equations involving logs and rationals

. . .

This session connects algebra with real business applications!

Rational Functions Deep Dive

Structure of Rational Functions

A rational function has the form:

\[f(x) = \frac{P(x)}{Q(x)}\]

where $P(x)$ and $Q(x)$ are polynomials and $Q(x) \neq 0$

Domain: All real numbers except where $Q(x) = 0$
Zeros: Where $P(x) = 0$ (and $Q(x) \neq 0$)
Vertical Asymptotes: Where $Q(x) = 0$ (canceling common factors)
Holes: Where both $P(x) = 0$ and $Q(x) = 0$ (canceled factors)
Horizontal/Oblique Asymptotes: Determined by degree comparison

What Are Asymptotes?

An asymptote is a line a function approaches

Think of it like a boundary the graph gets infinitely close to
Vertical asymptotes: Never crossed or touched (undefined there)
Horizontal/oblique asymptotes: Can be crossed at finite x-values, but approached as $x \to \pm\infty$
Three types: vertical, horizontal, and oblique (slanted)

Vertical Asymptotes

Occur where the denominator equals zero (and numerator doesn’t)

Mathematical definition: \[\lim_{x \to a^-} f(x) = \pm\infty \quad \text{or} \quad \lim_{x \to a^+} f(x) = \pm\infty\]

The function “blows up” (goes to $\infty$ or $-\infty$)
Graph has a vertical line at $x = a$
Function is undefined at this point
Example: $f(x) = \frac{1}{x}$ has vertical asymptote at $x = 0$

Horizontal Asymptotes

Describe the end behavior as $x \to \pm\infty$

Three cases based on degrees of $P(x)$ and $Q(x)$:

\[f(x) = \frac{2x + 1}{x^3 - 5}\]

Denominator grows faster
Horizontal asymptote: $y = 0$
The function approaches zero

\[f(x) = \frac{3x^2 + 2x - 1}{2x^2 + 5}\]

Both grow at same rate
Horizontal asymptote: $y = \frac{3}{2}$ (ratio of leading coefficients)

\[f(x) = \frac{x^3 + 2x}{x^2 - 1}\]

Numerator grows faster
No horizontal asymptote
May have an oblique (slanted) asymptote instead

Oblique (Slanted) Asymptotes

When degree of P exceeds degree of Q by exactly 1

Perform polynomial long division¹: $\frac{P(x)}{Q(x)} = L(x) + \frac{R(x)}{Q(x)}$
The quotient $L(x)$ (a linear function) is the oblique asymptote
As $x \to \pm\infty$, the remainder term $\frac{R(x)}{Q(x)} \to 0$

¹ No worries, no need to learn long division. This is just for the sake of completeness.

. . .

Example: $f(x) = \frac{x^2 + 1}{x - 1} = \frac{x^2 + 1}{x - 1} = x + 1 + \frac{2}{x-1}$

. . .

Oblique asymptote: $y = x + 1$

Holes vs. Asymptotes

Critical distinction when factors cancel!

Factor appears in both numerator and denominator
Example: $f(x) = \frac{(x-2)(x+1)}{(x-2)(x+3)}$
Factor $(x-2)$ cancels
Hole at $x = 2$, not an asymptote!
Simplified: $f(x) = \frac{x+1}{x+3}$, $x \neq 2$

Factor appears only in denominator
$f(x) = \frac{x+1}{x+3}$
Factor $(x+3)$ doesn’t cancel
Vertical asymptote at $x = -3$
Function undefined, goes to $\pm\infty$

. . .

Always factor completely and cancel common factors before identifying asymptotes!

Examples for Rational Functions

Asymptote Rules

Systematic Approach for Finding Asymptotes

Step 1: Factor completely \[f(x) = \frac{P(x)}{Q(x)} = \frac{\text{factored form}}{\text{factored form}}\]

Step 2: Cancel common factors → These create holes

Step 3: Vertical asymptotes → Remaining factors in denominator

Step 4: Horizontal/Oblique asymptotes → Compare degrees

Asymptote Analysis Challenge

3 minutes individual, 2 minutes pair discussion, 2 minutes class share

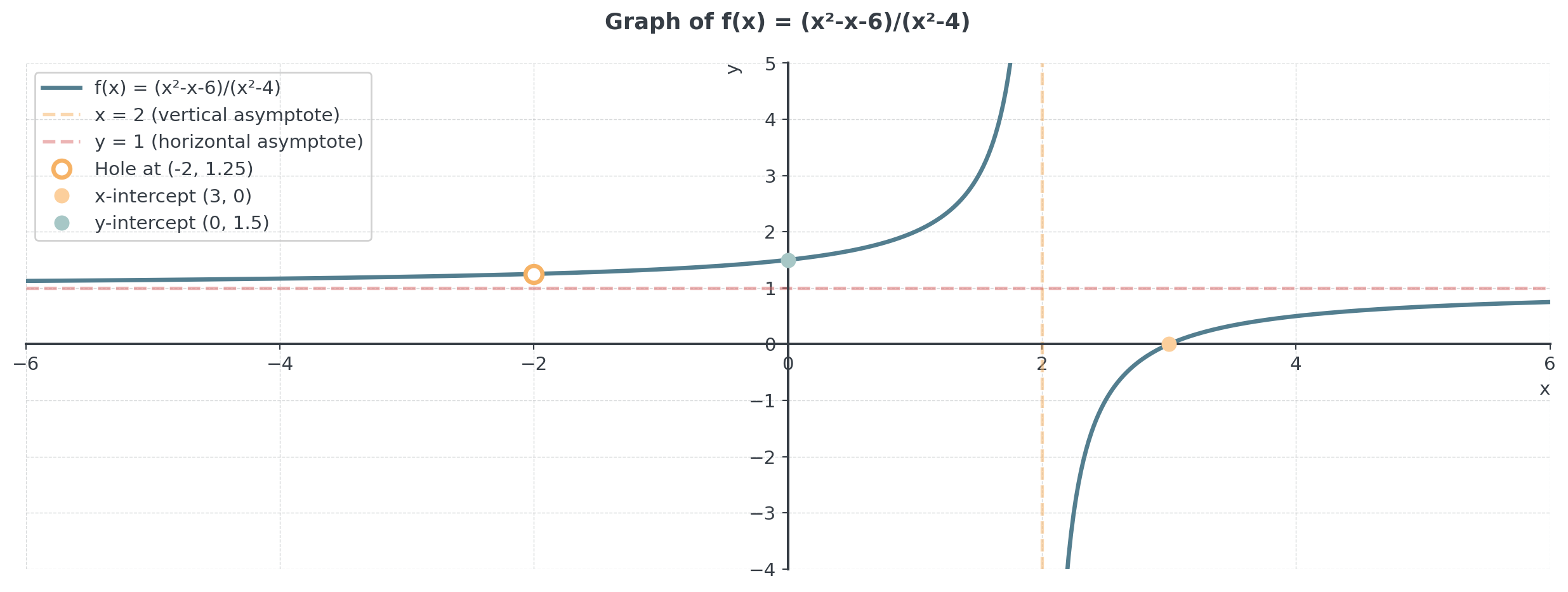
Analyze the function: $f(x) = \frac{x^2 - x - 6}{x^2 - 4}$

Your tasks:

Factor numerator and denominator
Identify any holes
Find all asymptotes
Determine x and y intercepts
Sketch a rough graph

Asymptote Analysis

Break - 10 Minutes

Business Application - Average Cost

Average Cost Functions

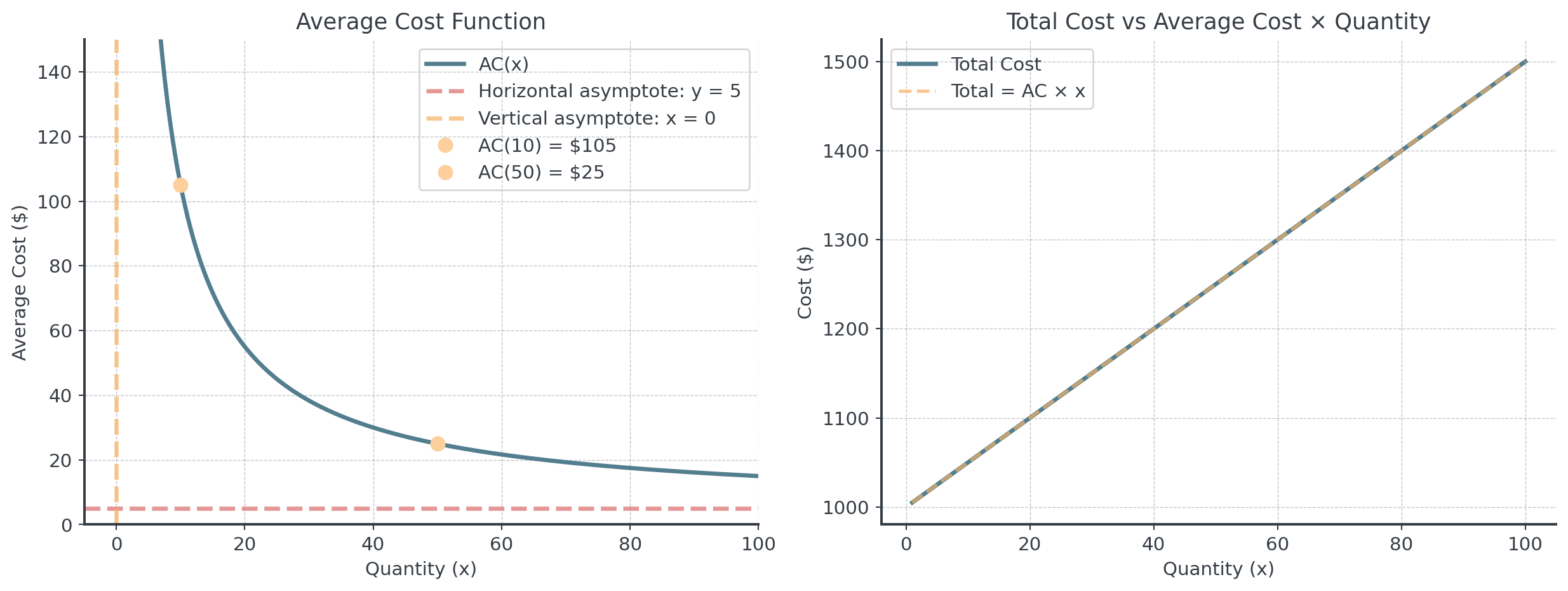
In business, the average cost per unit is:

\[AC(x) = \frac{\text{Total Cost}}{\text{Quantity}} = \frac{C(x)}{x} = \frac{F + vx}{x} = \frac{F}{x} + v\]

$F$ = Fixed costs
$v$ = Variable cost per unit
$x$ = Number of units

. . .

Do you get the idea here?

Key Properties

These functions often have the same properties:

Vertical asymptote at $x = 0$
Horizontal asymptote at $y = v$
Always decreasing for $x > 0$ (economies of scale)
Minimum average cost approaches $v$ as $x \to \infty$

. . .

Let’s see an example!

Visualization of Average Cost

Manufacturing Analysis

Work through this business scenario and then we compare

A company has fixed costs of $5000 per month and variable costs of $20 per unit.

Write the average cost function
Find the horizontal asymptote and interpret it
How many units minimize average cost to within $5 of the minimum?
Graph the function

Logarithmic Functions

Recap: Logarithm Properties

The Big Three Rules for Logarithms

Product Rule: $\log_b(xy) = \log_b(x) + \log_b(y)$
Quotient Rule: $\log_b(\frac{x}{y}) = \log_b(x) - \log_b(y)$
Power Rule: $\log_b(x^n) = n \cdot \log_b(x)$

. . .

Special Values

$\log_b(1) = 0$ for any base $b$
$\log_b(b) = 1$
$\log_b(b^n) = n$
$b^{\log_b(x)} = x$

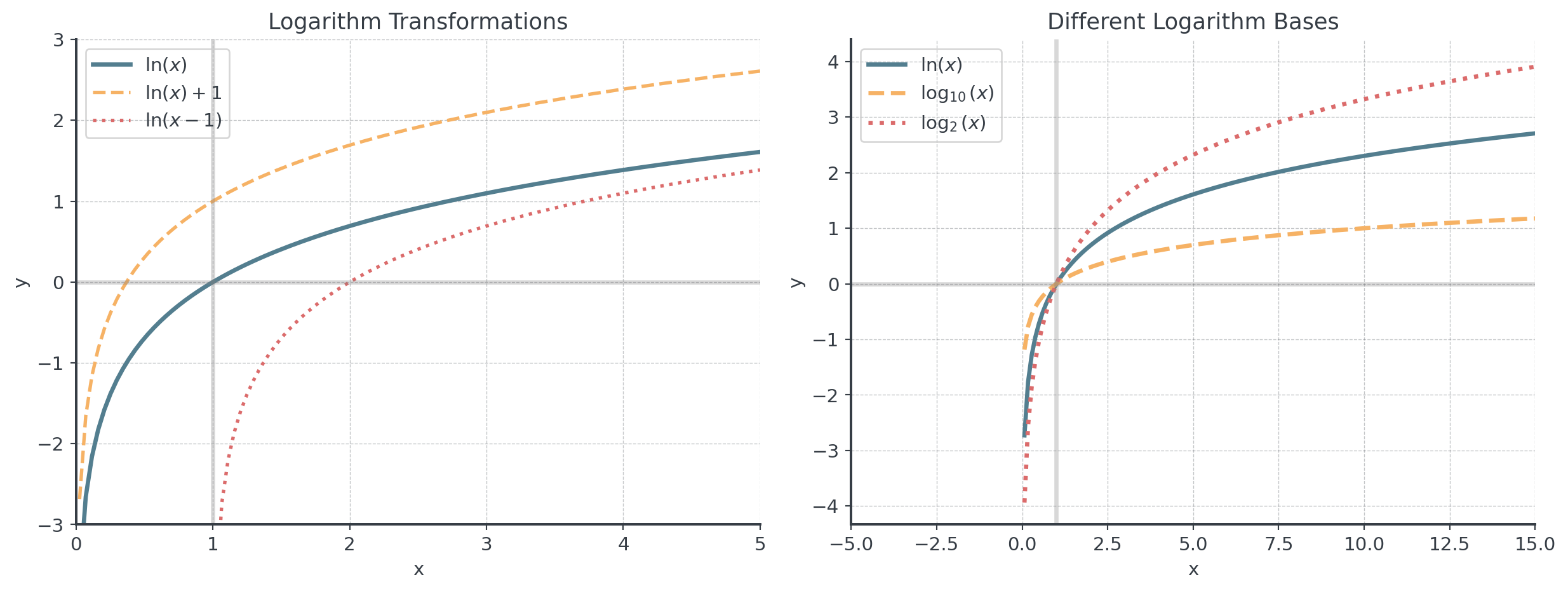
Logarithmic Transformations

Spot the Error: Logarithm Mistakes

Find and fix the errors!

Problem: Solve $\log_2(x) + \log_2(x - 2) = 3$

. . .

Student Solution:

“$\log_2(x) + \log_2(x - 2) = 3$

$\log_2(x + x - 2) = 3$

$\log_2(2x - 2) = 3$

$2x - 2 = 8$

$x = 5$”

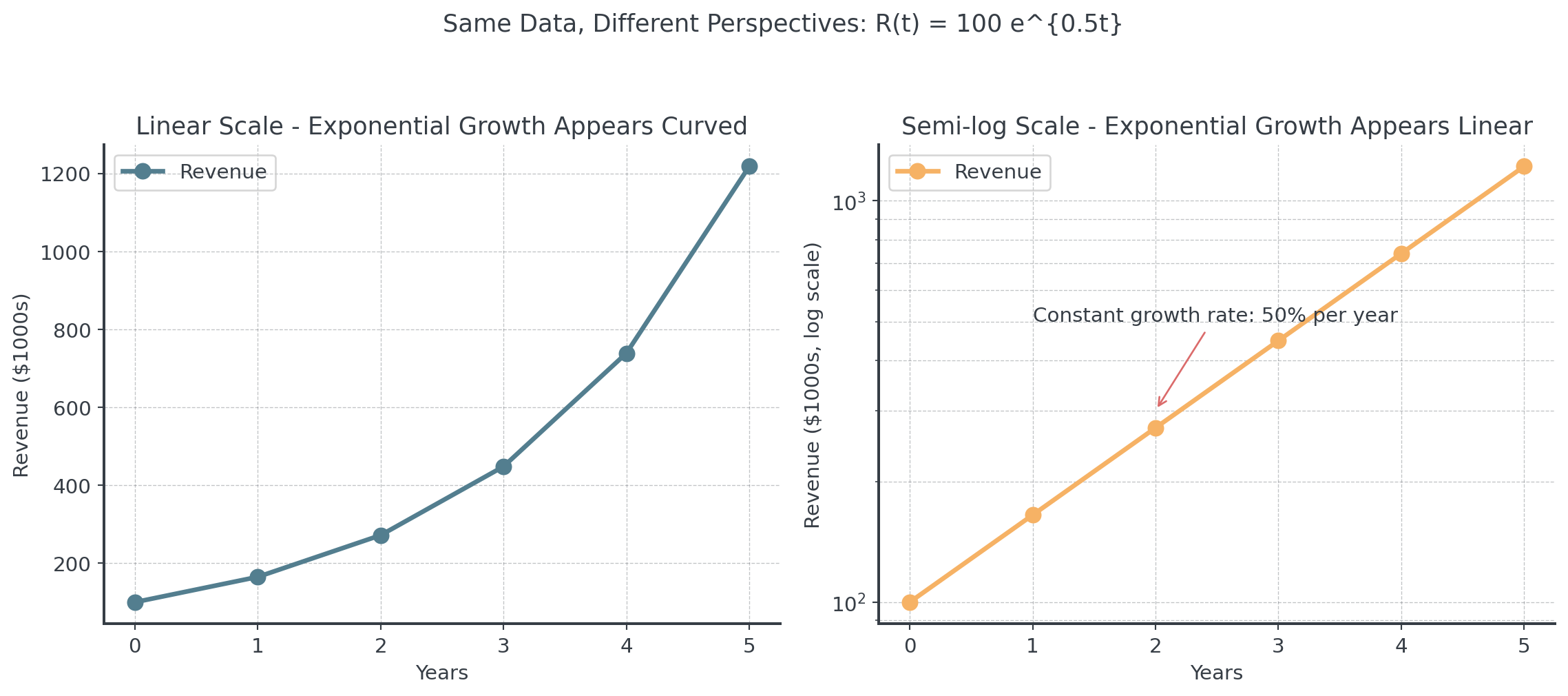
Semi-log and Log-log Plots

Semi-log Plot (y-axis log)

When data spans several orders of magnitude:

Exponential growth/decay patterns
Compound interest, population growth

. . .

Recognition:

Exponential functions appear as straight lines
Slope represents growth rate

Log-log Plot (both axes log)

When working with power law relationships:

Power law relationships
Allometric scaling
Economic relationships (supply/demand curves)

. . .

Recognition:

Power functions $y = ax^b$ appear as straight lines
Slope equals the exponent $b$

. . .

Let’s viusalize both!

Business Application: Market Analysis

Power Law Example: Production Costs

. . .

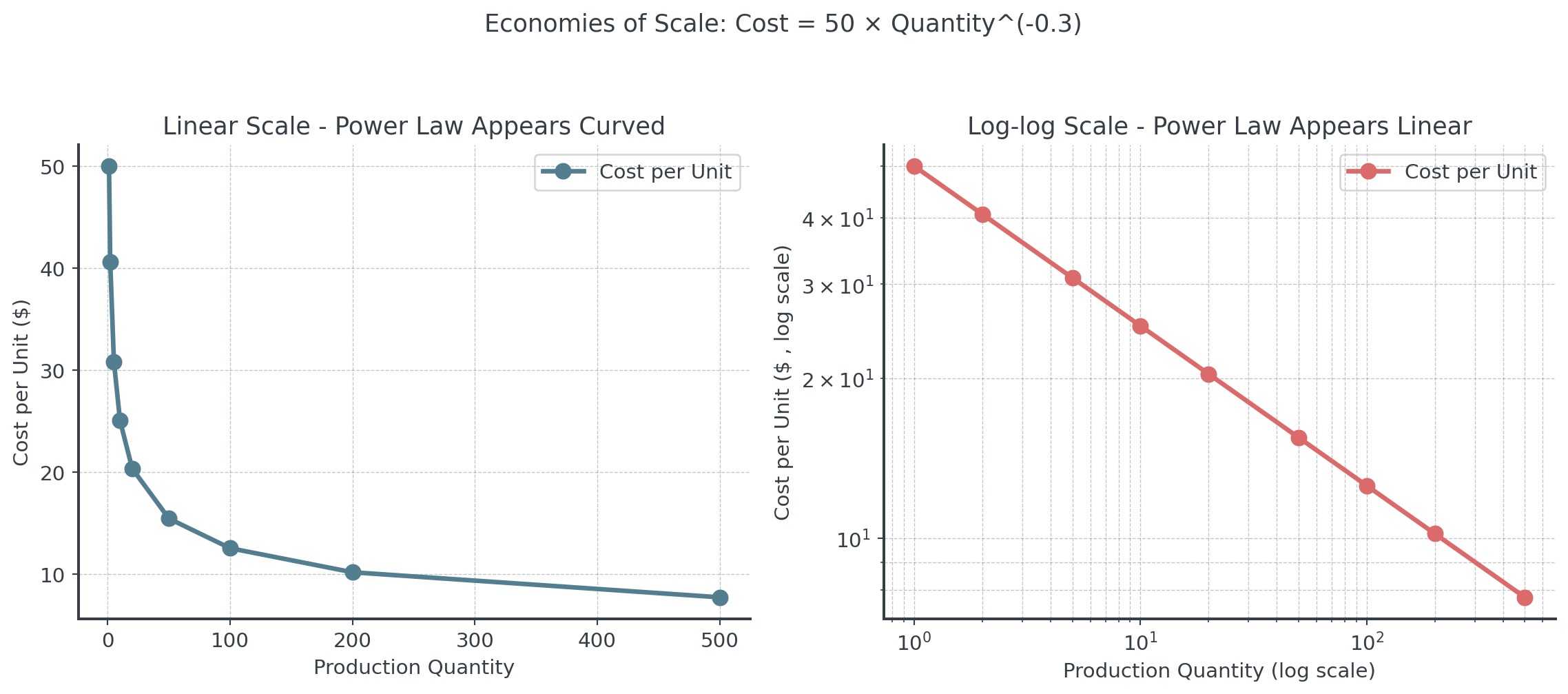
On the log-log plot, the straight line confirms a power law relationship. The slope of -0.3 means that doubling production reduces per-unit cost by about 19% (2^(-0.3) ≈ 0.81).

Guided Practice - 20 Minutes

Complex Problems

Work individually, then check with class

Rational Function: Analyze completely $f(x) = \frac{2x^2 - 8}{x^2 - x - 2}$
Logarithmic Equation: Solve $\ln(x + 3) - \ln(x - 1) = \ln(2)$
Multi-Step Challenge: A factory’s efficiency rating (as %) depends on production volume $x$ (in thousands of units per month, $x > 0$). \[E(x) = \frac{100(x^2 - 4x)}{x^2 - 8x + 20}\]
- Factor the numerator and find all zeros
- Find all asymptotes and interpret their meaning

Coffee Break - 15 Minutes

Synthesis & Applications

Real-World Application: pH Scale

Where logarithmic properties are important:

\[\text{pH} = -\log_{10}[\text{H}^+]\]

where $[\text{H}^+]$ is hydrogen ion concentration in mol/L

Domain: $(0, \infty)$ for concentration
Range: Typically 0-14 for pH
Each unit change = 10× concentration change
pH 7 is neutral ($[\text{H}^+] = 10^{-7}$)

Orange Juice

If orange juice has pH = 3.5:

. . .

Question: How much more acidic is orange juice compared to neutral water?

. . .

\[3.5 = -\log_{10}[\text{H}^+]\] \[[\text{H}^+] = 10^{-3.5} \approx 3.16 \times 10^{-4} \text{ mol/L}\]

. . .

This is 1000 times more acidic than neutral water!

Profit with Components I

A firm’s profit depends on portfolio size $x$ (number of clients):

\[P(x) = \frac{80x}{x + 5} - 15\ln(x + 1) + 10\]

Rational term $\frac{80x}{x+5}$: Revenue per client (approaches €80k asymptote)
Logarithmic term $-15\ln(x+1)$: Overhead & complexity costs
Fixed term $+10$: Base profit offset
Key insight: Logarithmic costs eventually erode the revenue gains
Critical question: What’s the optimal client portfolio size?

Profit with Components II

. . .

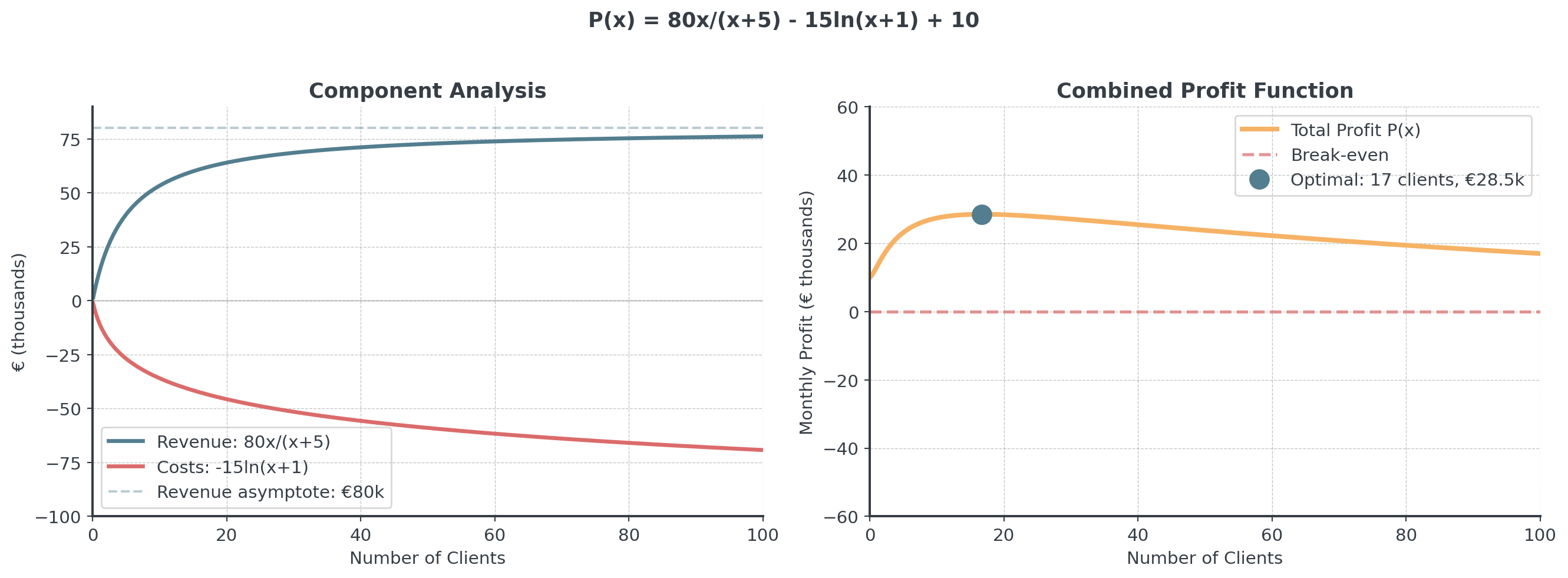
Initially, revenue growth outpaces cost growth → profits increase. Eventually, costs catch up and overtake revenue → profits decline!

Tasks - 15 Minutes

Function Investigation

Analyzes function types and then we dicuss

$f(x) = \frac{x^2 - 9}{x - 3}$
$AC(x) = \frac{2000 + 15x + 0.01x^2}{x}$
$g(t) = 50\ln(t + 2) - 100$
$h(x) = \frac{100}{x + 5} + \ln(x)$

. . .

Find domain and range
Identify all asymptotes/discontinuities
Describe a business application

Session Wrap-Up

Key Takeaways

Systematic asymptote finding through factoring
Distinguishing holes from vertical asymptotes
Business applications with average cost functions
Semi-log and log-log plots for data analysis
Rational functions model constrained optimization
Logarithms linearize exponential and power relationships
Combined functions capture complex business scenarios

Final Assessment - 10 Minutes

Quick Check

Work individually to test your understanding

Rational Function: Find all asymptotes and holes for: $f(x) = \frac{x^2 - 1}{x^2 + x - 2}$
Logarithmic Equation: Solve: $2\ln(x) - \ln(x + 6) = \ln(4)$

Homework Preview

Tasks 04-06

You’ll practice:

Complete rational function analysis (find all features)
Logarithmic equation solving using properties
Business optimization with average cost
Data interpretation with different scales
Synthesis problems combining both function types

. . .

Success Strategy: Always factor rational functions first as it reveals everything!

Mock Exam Strategies

What’s important for the Mock Exam

Read carefully: Every word and number matters
Show all work: Partial credit is available for clear methodology
Label everything: Variables, units, and graph features
Check domains: Especially for logarithmic and rational functions
Verify solutions: Substitute back when possible

. . .

This exam tests your mastery functions. Apply the systematic methods we’ve practiced!