Session 06-01 - Antiderivatives & Indefinite Integrals

Section 06: Integral Calculus

Author

Dr. Nikolai Heinrichs & Dr. Tobias Vlćek

Entry Quiz - 10 Minutes

Quick Review from Section 05

Test your understanding of Differential Calculus

Find \(f'(x)\) for \(f(x) = 3x^4 - 2x^2 + 5x - 7\)
A profit function is \(P(x) = -x^2 + 80x - 400\). Find the production level that maximizes profit.
For \(g(x) = x^3 - 6x^2 + 9x + 1\), find all critical points and classify them.
If \(C'(x) = 6x + 10\) represents marginal cost, what does \(C'(5) = 40\) mean in business terms?

Homework Discussion - 15 Minutes

Your questions from Section 05

Focus on differential calculus applications

Challenges with optimization problems
Curve sketching and second derivative test
Function determination (Funktionsscharen)
Any remaining questions before we move forward

. . .

Today we begin Integral Calculus - the reverse of differentiation!

Learning Objectives

What You’ll Master Today

Understand the antiderivative concept as reversing differentiation
Apply the power rule for integration: \(\int x^n \, dx\)
Use sum and constant rules to integrate polynomials
Interpret the constant of integration (+C) and families of functions
Solve initial value problems to find specific antiderivatives
Verify antiderivatives by differentiation
Apply integration to business (marginal cost → total cost)

. . .

Integration is the reverse of differentiation - today we learn to “undo” derivatives!

Part A: The Antiderivative Concept

From Derivatives to Antiderivatives

Remember differentiation?

\[f(x) = x^3 \quad \xrightarrow{\text{differentiate}} \quad f'(x) = 3x^2\]

. . .

Now we reverse the process:

\[F'(x) = 3x^2 \quad \xleftarrow{\text{antidifferentiate}} \quad F(x) = x^3\]

. . .

Definition: Antiderivative (Stammfunktion)

\(F(x)\) is an antiderivative of \(f(x)\) if \(F'(x) = f(x)\).

In German: \(F\) is the Stammfunktion of \(f\).

The Question We’re Solving

Given a derivative, find the original function

. . .

Example Questions:

If \(f'(x) = 2x\), what could \(f(x)\) be?
If the marginal cost is \(C'(x) = 50\), what is the total cost function?
If velocity is \(v(t) = 3t^2\), what is the position function?

. . .

Business Context: We often know the rate of change (marginal cost, growth rate) and need to find the total quantity (total cost, population).

Finding: First Examples

Question: If \(F'(x) = 2x\), what is \(F(x)\)?

. . .

Think: What function, when differentiated, gives \(2x\)?

If \(F(x) = x^2\), then \(F'(x) = 2x\) ✓
But also: \(F(x) = x^2 + 5\) gives \(F'(x) = 2x\) ✓
And: \(F(x) = x^2 - 100\) gives \(F'(x) = 2x\) ✓

. . .

Problem: There are infinitely many antiderivatives!

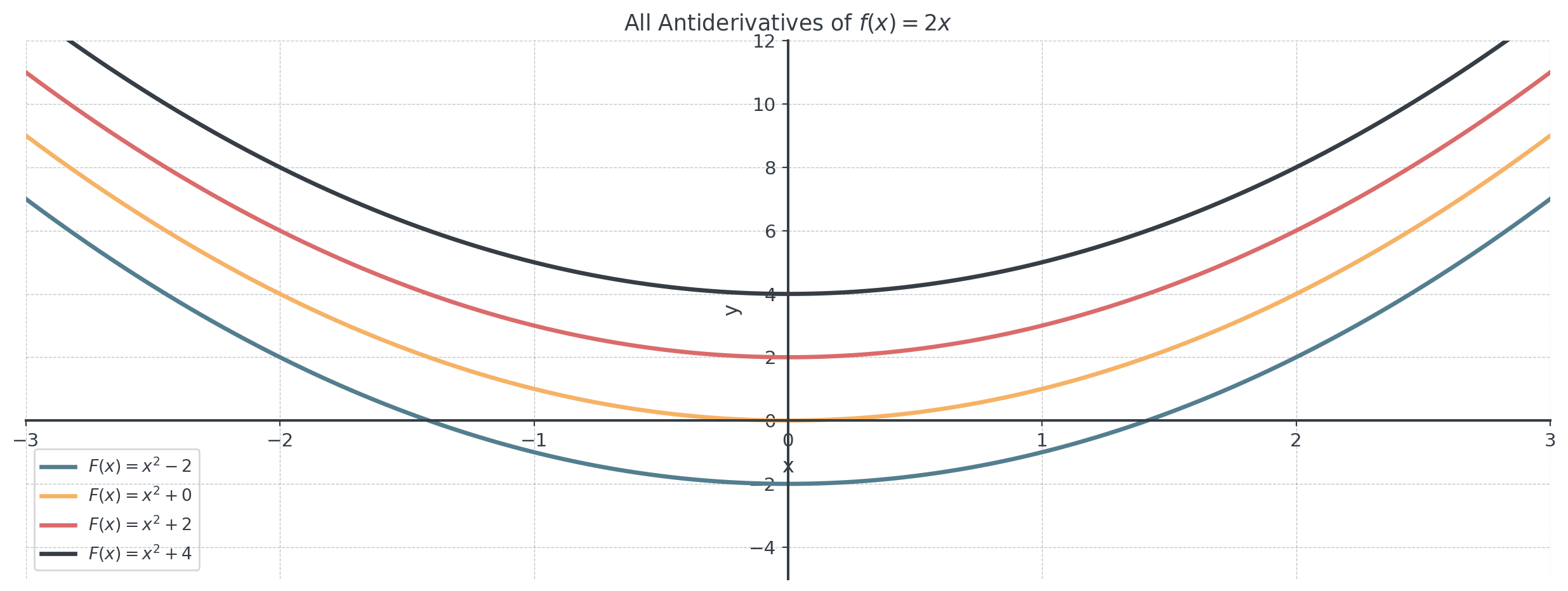
The Family of Antiderivatives

. . .

All these curves have the same slope at each x-value!

The Constant of Integration

Solution: We write the general antiderivative with a constant \(C\):

. . .

\[\int 2x \, dx = x^2 + C\]

. . .

The symbol \(\int\) means “integrate” (find the antiderivative)
\(dx\) indicates we integrate with respect to \(x\)
\(+C\) represents any constant (the constant of integration)
This notation is called an indefinite integral

. . .

Always include +C for indefinite integrals!

Part B: The Power Rule for Integration

Reversing the Power Rule

Recall the power rule for derivatives:

\[\frac{d}{dx}[x^n] = nx^{n-1}\]

. . .

Reverse it for integration:

\[\int x^n \, dx = \frac{x^{n+1}}{n+1} + C \quad \text{for } n \neq -1\]

. . .

Memory trick: “Add 1 to the power, divide by the new power”

Power Rule Examples

Example 1: \(\int x^3 \, dx\)

. . .

\[\int x^3 \, dx = \frac{x^{3+1}}{3+1} + C = \frac{x^4}{4} + C\]

. . .

Check: \(\frac{d}{dx}\left[\frac{x^4}{4} + C\right] = \frac{4x^3}{4} = x^3\) ✓

. . .

Example 2: \(\int x^5 \, dx\)

. . .

\[\int x^5 \, dx = \frac{x^6}{6} + C\]

Special Cases

Constant function: \(\int 1 \, dx\) (or \(\int dx\))

. . .

Think of \(1 = x^0\): \[\int x^0 \, dx = \frac{x^{0+1}}{0+1} + C = x + C\]

. . .

Linear function: \(\int x \, dx\)

\[\int x^1 \, dx = \frac{x^2}{2} + C\]

. . .

The antiderivative of a constant is a line, the antiderivative of \(x\) is a parabola.

Negative and Fractional Powers

Negative powers: \(\int x^{-2} \, dx\)

. . .

\[\int x^{-2} \, dx = \frac{x^{-2+1}}{-2+1} + C = \frac{x^{-1}}{-1} + C = -\frac{1}{x} + C\]

. . .

Fractional powers: \(\int x^{1/2} \, dx = \int \sqrt{x} \, dx\)

. . .

\[\int x^{1/2} \, dx = \frac{x^{3/2}}{3/2} + C = \frac{2x^{3/2}}{3} + C = \frac{2\sqrt{x^3}}{3} + C\]

. . .

The power rule fails when \(n = -1\) (we would divide by zero). We’ll handle \(\int \frac{1}{x} \, dx\) later.

Part C: Sum and Constant Multiple Rules

Constant Multiple Rule

If \(k\) is a constant:

\[\int k \cdot f(x) \, dx = k \cdot \int f(x) \, dx\]

. . .

Example: \(\int 5x^3 \, dx\)

. . .

\[\int 5x^3 \, dx = 5 \int x^3 \, dx = 5 \cdot \frac{x^4}{4} + C = \frac{5x^4}{4} + C\]

. . .

Pull constants outside the integral, then integrate!

Sum and Difference Rules

For sums and differences:

\[\int [f(x) \pm g(x)] \, dx = \int f(x) \, dx \pm \int g(x) \, dx\]

. . .

Example: \(\int (x^2 + 3x - 5) \, dx\)

. . .

\[= \int x^2 \, dx + \int 3x \, dx - \int 5 \, dx\]

. . .

\[= \frac{x^3}{3} + 3 \cdot \frac{x^2}{2} - 5x + C = \frac{x^3}{3} + \frac{3x^2}{2} - 5x + C\]

Polynomial Integration

Example: \(\int (4x^3 - 6x^2 + 2x - 7) \, dx\)

\(\int 4x^3 \, dx = 4 \cdot \frac{x^4}{4} = x^4\)
\(\int 6x^2 \, dx = 6 \cdot \frac{x^3}{3} = 2x^3\)
\(\int 2x \, dx = 2 \cdot \frac{x^2}{2} = x^2\)
\(\int 7 \, dx = 7x\)

. . .

Answer: \(\int (4x^3 - 6x^2 + 2x - 7) \, dx = x^4 - 2x^3 + x^2 - 7x + C\)

. . .

Check: \(\frac{d}{dx}[x^4 - 2x^3 + x^2 - 7x + C] = 4x^3 - 6x^2 + 2x - 7\) ✓

Practice - 10 Minutes

Practice: Basic Integration

Work individually for 3 minutes

Find the following antiderivatives:

\(\int 6x^2 \, dx\)
\(\int (x^4 - 3x^2 + 1) \, dx\)
\(\int \frac{4}{x^3} \, dx\) (rewrite as power first)
\(\int (2\sqrt{x} + 3) \, dx\)

Integration Drill

Work in pairs

Evaluate these integrals and verify by differentiation:

\(\int (3x^2 + 4x + 5) \, dx\)
\(\int (x^3 - 2x + 4) \, dx\)
\(\int 10x^4 \, dx\)
\(\int \left(x^2 + \frac{1}{x^2}\right) \, dx\)

Break - 10 Minutes

Part D: Initial Value Problems

Finding a Specific Antiderivative

Problem: The general antiderivative has infinitely many solutions. How do we find a specific one?

. . .

Solution: Use an initial condition, a known point on the function.

Given \(f'(x)\) and a condition like \(f(a) = b\)
Find the specific function \(f(x)\).

. . .

Steps:

Find the general antiderivative with \(+C\)
Substitute the initial condition to solve for \(C\)
Write the specific solution

Example: Initial Value Problem

Problem: Find \(f(x)\) if \(f'(x) = 6x^2 - 4\) and \(f(1) = 5\).

. . .

Step 1: Find the general antiderivative

. . .

\[f(x) = \int (6x^2 - 4) \, dx = 2x^3 - 4x + C\]

. . .

Step 2: Use the initial condition \(f(1) = 5\)

. . .

\[f(1) = 2(1)^3 - 4(1) + C = 5; C = 7\]

. . .

Step 3: Write the specific solution

. . .

\[f(x) = 2x^3 - 4x + 7\]

Visualizing the Initial Condition

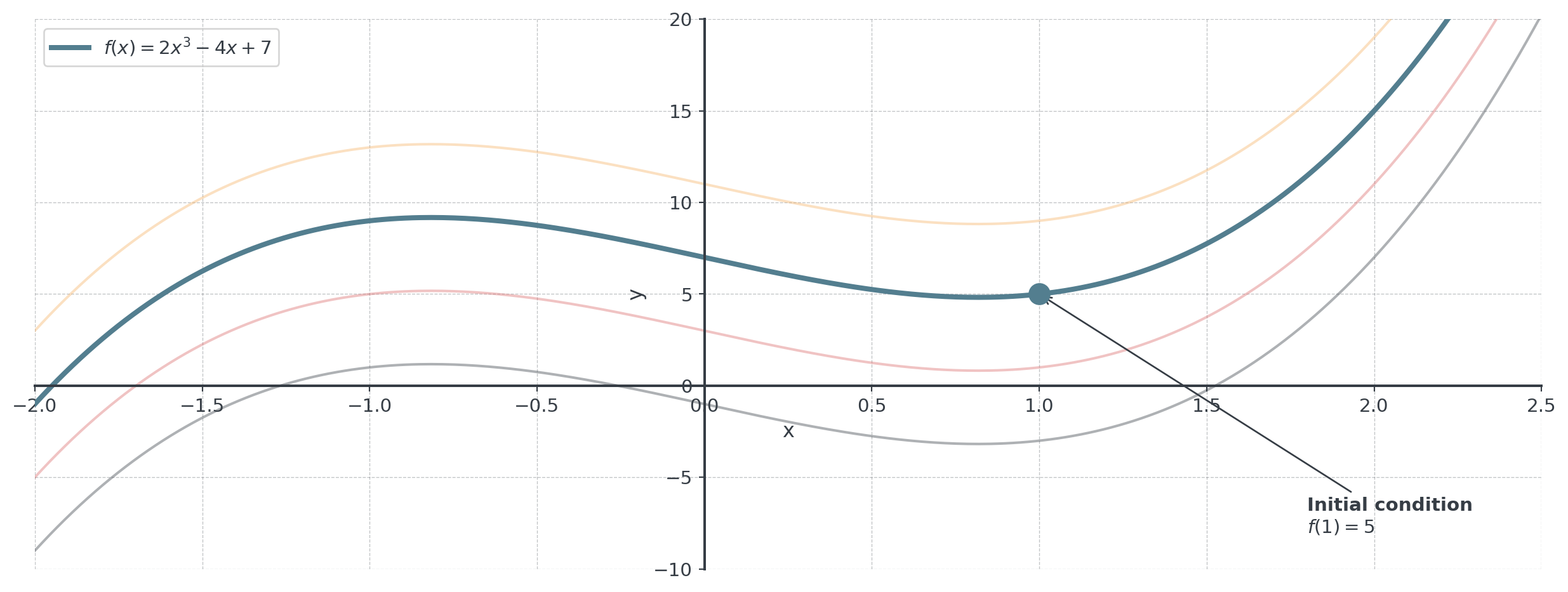
The initial condition selects one curve from the family!

Total Cost from Marginal Cost

Scenario: A manufacturing company knows its marginal cost function:

\[MC(x) = C'(x) = 0.3x^2 - 2x + 50\]

The fixed costs are €1,000 (cost when producing 0 units).

. . .

Question: Find the total cost function \(C(x)\).

. . .

Step 1: Integrate marginal cost

. . .

\[C(x) = \int (0.3x^2 - 2x + 50) \, dx = 0.1x^3 - x^2 + 50x + C\]

Completing the Business Problem

Step 2: Use the initial condition \(C(0) = 1000\)

. . .

\[C(0) = 0.1(0)^3 - (0)^2 + 50(0) + C = 1000\] \[C = 1000\]

. . .

Step 3: Final answer

\[C(x) = 0.1x^3 - x^2 + 50x + 1000\]

. . .

The constant \(C\) represents the fixed costs, costs that don’t depend on production level.

Visualizing Cost Functions

. . .

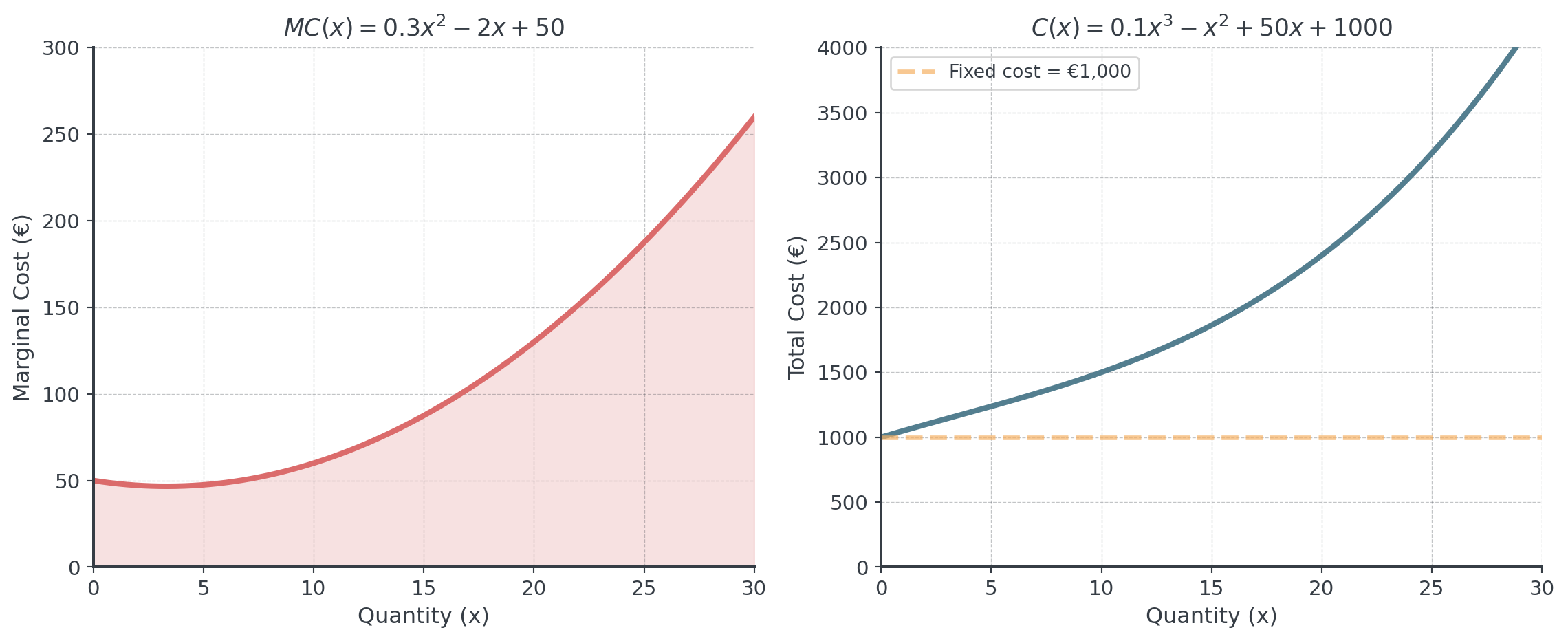
The marginal cost (derivative) shows the rate; the total cost (antiderivative) shows the accumulated total.

Part E: Velocity and Position

Application: Motion

Key relationships:

Position: \(s(t)\) = where the object is
Velocity: \(v(t) = s'(t)\) = rate of change of position
Acceleration: \(a(t) = v'(t) = s''(t)\) = rate of change of velocity

. . .

Reversing the relationships:

If you know velocity, integrate to find position: \(s(t) = \int v(t) \, dt\)
If you know acceleration, integrate to find velocity: \(v(t) = \int a(t) \, dt\)

Finding Position from Velocity

Problem: A car’s velocity is \(v(t) = 3t^2 + 2t\) m/s, where \(t\) is in seconds. At \(t = 0\), the car is at \(s = 10\) meters. Find the position function \(s(t)\).

. . .

Step 1: Integrate velocity to get position

. . .

\[s(t) = \int (3t^2 + 2t) \, dt = t^3 + t^2 + C\]

. . .

Step 2: Use initial condition \(s(0) = 10\)

. . .

\[s(0) = 0 + 0 + C = 10 \implies C = 10\]

. . .

\[s(t) = t^3 + t^2 + 10\]

Verifying Our Answer

Check: Does \(s'(t) = v(t)\)?

. . .

\[s(t) = t^3 + t^2 + 10\] \[s'(t) = 3t^2 + 2t = v(t) \quad \checkmark\]

. . .

Check: Does \(s(0) = 10\)?

. . .

\[s(0) = 0 + 0 + 10 = 10 \quad \checkmark\]

. . .

Always check your antiderivative by differentiating to recover the original function and substituting the initial condition!

Guided Practice - 20 Minutes

Practice Set A: Basic Antiderivatives

Work individually for 5 minutes

Find the following indefinite integrals:

\(\int (5x^4 - 3x^2 + 2) \, dx\)
\(\int (x^3 + x^{-1/2}) \, dx\)
\(\int \frac{6}{x^4} \, dx\)
\(\int (4\sqrt{x} - \frac{3}{x^2}) \, dx\)

Practice Set B: Initial Value Problems

Work individually for 7 minutes

Solve these initial value problems:

\(f'(x) = 4x^3 - 6x\), \(f(2) = 10\). Find \(f(x)\).
\(g'(x) = 3x^2 + 4\), \(g(0) = 5\). Find \(g(x)\).
The marginal revenue is \(MR(x) = 100 - 2x\). Revenue is €0 when no units are sold. Find \(R(x)\).

Practice Set C: Business Applications

Work in pairs for 8 minutes

A company’s marginal cost is \(MC(x) = 20 + 0.4x\) euros per unit. Fixed costs are €500. Find the total cost function \(C(x)\) and calculate the total cost of producing 50 units.
A product’s marginal profit is \(MP(x) = 80 - 4x\) euros per unit. The company breaks even (profit = 0) when selling 0 units. Find the profit function \(P(x)\) and determine how many units maximize profit.

Coffee Break - 15 Minutes

Business Applications Deep Dive

From Rates to Totals

Integration connects rates of change to accumulated totals:

Rate Function (Derivative)	Total Function (Antiderivative)
Marginal cost \(C'(x)\)	Total cost \(C(x)\)
Marginal revenue \(R'(x)\)	Total revenue \(R(x)\)
Marginal profit \(P'(x)\)	Total profit \(P(x)\)
Production rate	Total production
Growth rate	Total quantity

. . .

The constant of integration often represents a fixed quantity (fixed costs, initial inventory, starting capital).

Example: Complete Cost Analysis

Scenario: A furniture manufacturer has:

Marginal cost: \(MC(x) = 0.02x^2 - 2x + 100\) euros per unit
Fixed costs: €5,000
Each unit sells for €150

. . .

Tasks:

Find the total cost function \(C(x)\)
Find the revenue function \(R(x)\)
Find the profit function \(P(x)\)
Determine the break-even points

Solution Part 1: Cost Function

Step 1: Integrate marginal cost

\[C(x) = \int (0.02x^2 - 2x + 100) \, dx\]

. . .

\[C(x) = \frac{0.02x^3}{3} - x^2 + 100x + C\]

. . .

Step 2: Apply initial condition \(C(0) = 5000\)

\[C = 5000\]

. . .

Answer: \(C(x) = \frac{x^3}{150} - x^2 + 100x + 5000\)

Solution Part 2: Revenue and Profit

Revenue: (Price × Quantity)

\[R(x) = 150x\]

. . .

Profit: (Revenue − Cost)

\[P(x) = R(x) - C(x)\]

\[P(x) = 150x - \left(\frac{x^3}{150} - x^2 + 100x + 5000\right)\]

. . .

\[P(x) = -\frac{x^3}{150} + x^2 + 50x - 5000\]

Visualizing the Business Model

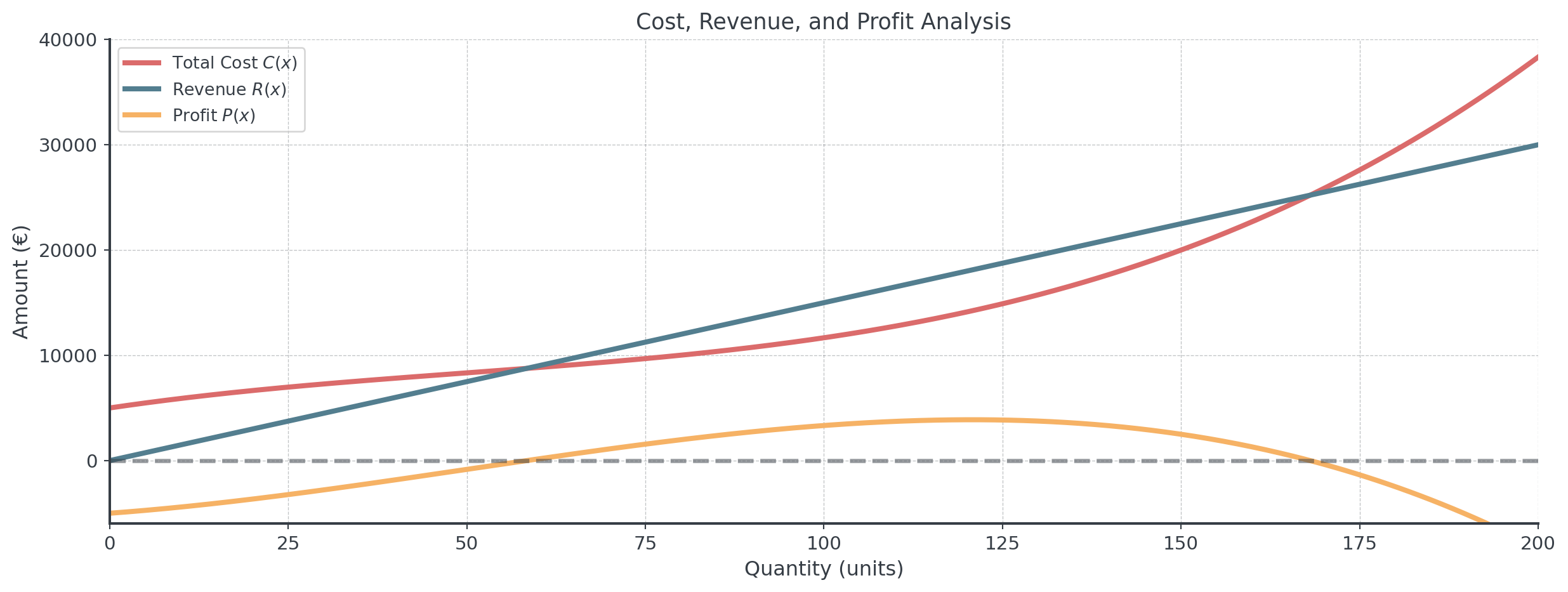
Collaborative Problem-Solving

Group Challenge: Startup Analysis

Scenario: A tech startup is launching a new app. Their data analytics team has modeled:

Marginal cost (per user): \(MC(x) = 0.01x + 5\) euros, where \(x\) is thousands of users

Fixed costs: €50,000 (servers, development, etc.)

Revenue per user: €12 per thousand users

Group Challenge: Tasks

Work in groups and then we compare

Find the total cost function \(C(x)\) for \(x\) thousand users
Find the revenue function \(R(x)\)
Find the profit function \(P(x)\)
Calculate the profit/loss at 1,000 users, 5,000 users, and 10,000 users
Find the break-even point(s)
At what user count is profit maximized?

Wrap-Up & Key Takeaways

Today’s Essential Concepts

Antiderivative: If \(F'(x) = f(x)\), then \(F(x)\) is antiderivative of \(f(x)\)
Power rule: \(\int x^n \, dx = \frac{x^{n+1}}{n+1} + C\) (for \(n \neq -1\))
Sum/Constant rules: Split integrals, pull out constants
+C is essential: Represents the family of all antiderivatives
Initial conditions: Fix the value of \(C\) to find a specific function
Verification: Always differentiate to check your answer

. . .

Next session: We’ll learn about definite integrals and the Fundamental Theorem of Calculus!

Integration Formulas Summary

Function	Antiderivative
\(x^n\) (\(n \neq -1\))	\(\frac{x^{n+1}}{n+1} + C\)
\(k\) (constant)	\(kx + C\)
\(kf(x)\)	\(k \int f(x) \, dx\)
\(f(x) \pm g(x)\)	\(\int f(x) \, dx \pm \int g(x) \, dx\)

. . .

Integration is “undo-ing” differentiation. Ask yourself: “What function, when differentiated, gives me this?”

Final Assessment - 5 Minutes

Quick Check

Work individually, then compare

Find \(\int (2x^3 - 5x + 3) \, dx\)
Given \(f'(x) = 6x - 2\) and \(f(1) = 4\), find \(f(x)\).
A company’s marginal cost is \(MC(x) = 30 + 0.5x\). Fixed costs are €200. What is the cost of producing 20 units?

Next Session Preview

Coming Up: Definite Integrals & FTC

The definite integral as a signed area
The Fundamental Theorem of Calculus
Evaluating integrals using \(F(b) - F(a)\)
Properties of definite integrals
Applications to accumulated quantities

. . .

Complete Tasks 06-01

Practice basic antiderivatives until they’re automatic
Work through initial value problems
Focus on business applications (cost, revenue, profit)