Session 03-03 - Quadratic Functions & Basic Optimization
Section 03: Functions as Business Models
Entry Quiz - 10 Minutes
Review from Session 03-02
Work individually, then we discuss together as group
Find the market equilibrium for:
- Demand: \(Q_d = 200 - 2p\)
- Supply: \(Q_s = 50 + 3p\)
Write the equation of a line passing through points (2, 8) and (5, 20).
For the cost function \(C(x) = 500 + 12x\) and revenue \(R(x) = 25x\), find the profit when \(x = 100\).
Homework Review - 20 Minutes
Discussing Tasks 03-02
Let’s discuss the most difficult tasks from last lecture
- Problem 5: Market competition analysis
- How did you determine the break-even data usage?
- Problem 6: Production planning with constraints
- Challenges with multiple constraints?
- Problem 7: Dynamic pricing (if attempted)
- What price seemed optimal in your testing?
. . .
Today we’ll learn the exact method to find that optimal price!
Introduction to Quadratic Functions
From Linear to Quadratic
Quadratic functions model accelerating change
. . .
Linear vs. Quadratic:
- Linear: \(f(x) = mx + b\) → Constant rate of change
- Quadratic: \(f(x) = ax^2 + bx + c\) → Changing rate of change
- Graph shape: Quadratic → Parabola (U-shaped or ∩-shaped)
- Business meaning:
- Linear → Fixed relationships
- Quadratic → Optimization opportunities!
Standard Form
The foundation: f(x) = ax² + bx + c
Key components:
- a: Direction and width
- \(a > 0\): Opens upward (has minimum)
- \(a < 0\): Opens downward (has maximum)
- \(|a|\) larger → Narrower parabola
- b: Affects position of vertex
- c: y-intercept (value when \(x = 0\))
Example: Profit Function
Quick Practice - 10 Minutes
Work individually, then we discuss
- Determine: Does it open upward (U) or downward (∩)?
- Determine: Does it have a maximum or minimum?
- Determine: What is the y-intercept?
\(R(x) = -3x^2 + 120x - 500\)
\(C(x) = 2x^2 + 40x + 1000\)
\(P(x) = -x^2 + 50x - 300\)
Challenge: For c. find the break-even points.
Break - 10 Minutes
Finding the Vertex
The Vertex Formula
The key: x = -b/2a
For \(f(x) = ax^2 + bx + c\):
- Vertex x-coordinate: \(x_v = -\frac{b}{2a}\)
- Vertex y-coordinate: \(f(x_v) = f(-\frac{b}{2a})\)
- Vertex represents:
- Maximum if \(a < 0\) (parabola opens down)
- Minimum if \(a > 0\) (parabola opens up)
- Axis of symmetry: Vertical line \(x = x_v\)
Vertex Example: Revenue Optimization
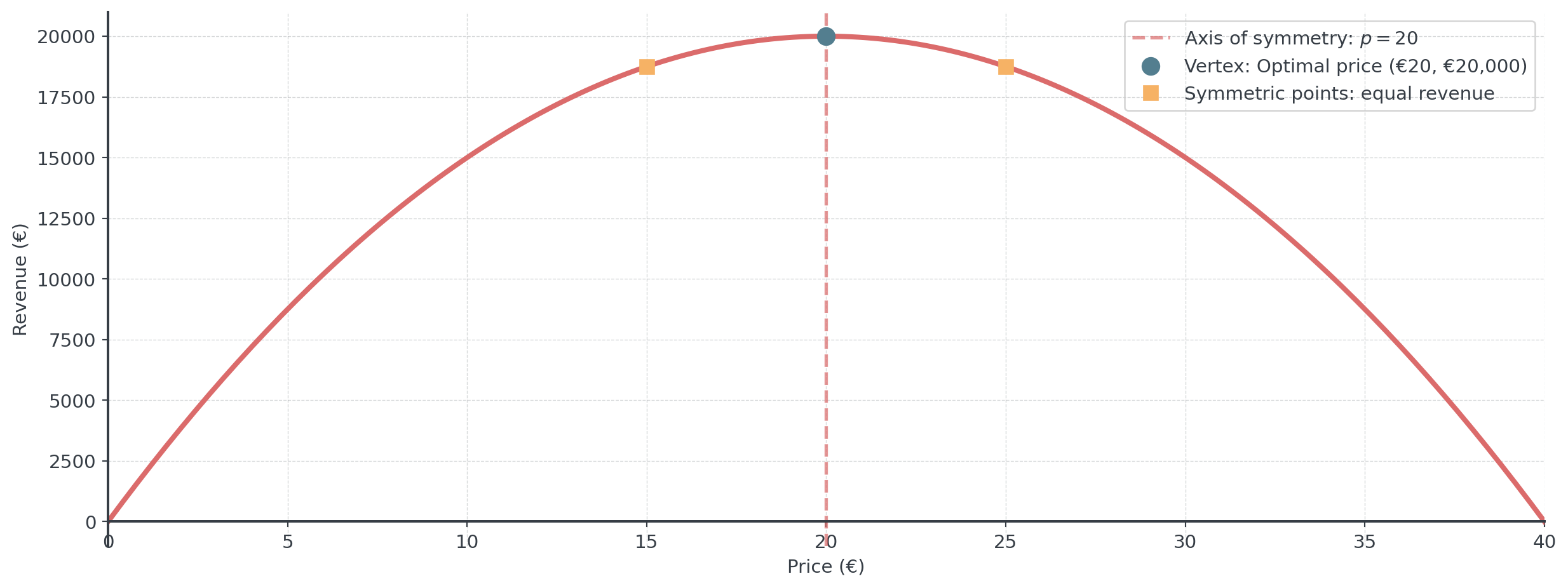
A company’s revenue depends on price:
\[R(p) = -50p^2 + 2000p\]
- Find optimal price: \(p_v = -\frac{2000}{2(-50)} = -\frac{2000}{-100} = 20\) euros
- Maximum revenue: \(R(20) = 20000\) euros
- Interpretation: Charging €20 maximizes revenue at €20,000
. . .
The axis of symmetry divides the parabola into mirror images. Points equidistant from it have equal revenue!
Visualization
Vertex Form
Alternative representation: f(x) = a(x - h)² + k
- Vertex: \((h, k)\) - directly visible!
- Direction: \(a\) (same as standard form)
- Advantage: Vertex immediately apparent
- Transformation from vertex:
- Horizontal shift by \(h\)
- Vertical shift by \(k\)
- Example: \(f(x) = 2(x - 3)^2 + 5\) → Vertex at \((3, 5)\), minimum
- Example: \(g(x) = -(x + 4)^2 + 10\) → Vertex at \((-4, 10)\), maximum
Completing the Square
Converting to Vertex Form
Transform \(f(x) = ax^2 + bx + c\) to \(f(x) = a(x - h)^2 + k\)
. . .
Process:
- Factor out \(a\) from first two terms
- Complete the square inside parentheses
- Simplify to vertex form
. . .
Sorry, I know I said we don’t need that!
Step-by-Step Example
Convert \(f(x) = 2x^2 - 12x + 10\) to vertex form
- Factor out 2: \(f(x) = 2(x^2 - 6x) + 10\)
- Complete square: Need \((\frac{-6}{2})^2 = 9\)
- Add and subtract: \(f(x) = 2(x^2 - 6x + 9 - 9) + 10\)
- Rewrite: \(f(x) = 2((x - 3)^2 - 9) + 10\)
- Distribute: \(f(x) = 2(x - 3)^2 - 18 + 10\)
- Final form: \(f(x) = 2(x - 3)^2 - 8\)
- Vertex: \((3, -8)\) with minimum value -8
Fast Exercise
Solve in 5 minutes, then we compare solutions
Convert \(f(x) = 3x^2 + 18x + 20\) to vertex form by completing the square.
Business Applications
Price-Dependent Demand
When price affects quantity: Revenue becomes quadratic!
Basic Scenario:
- Demand function: \(Q = a - bp\) (quantity depends on price)
- Revenue: \(R = p \times Q = p(a - bp)\)
- Expanded: \(R(p) = ap - bp^2 = -bp^2 + ap\)
- This is quadratic in \(p\)!
. . .
Remember, we have seen this in the past!
Example: Concert Venue
A venue (capacity: 1000) has ticket demand: \(Q = 1000 - 20p\)
- Revenue function: \(R(p) = p(1000 - 20p) = 1000p - 20p^2\)
- Optimal price: \(p^* = -\frac{1000}{2(-20)} = \frac{1000}{40} = 25\) euros
- Tickets sold: \(Q = 1000 - 20(25) = 500\)
- Maximum revenue: \(R(25) = 25 \times 500 = 12,500\)
- At €0: Demand = 1000 (full capacity if free)
- At €50: Demand = 0 (too expensive, no one buys)
. . .
Note: This maximizes revenue, not necessarily profit!
Guided Practice - 20 Minutes
Individual Exercise Block
Work alone for 15 minutes, then we compare solutions
- For \(f(x) = x^2 - 8x + 12\):
- Find the vertex using the formula
- Determine if it’s a maximum or minimum and find the y-intercept
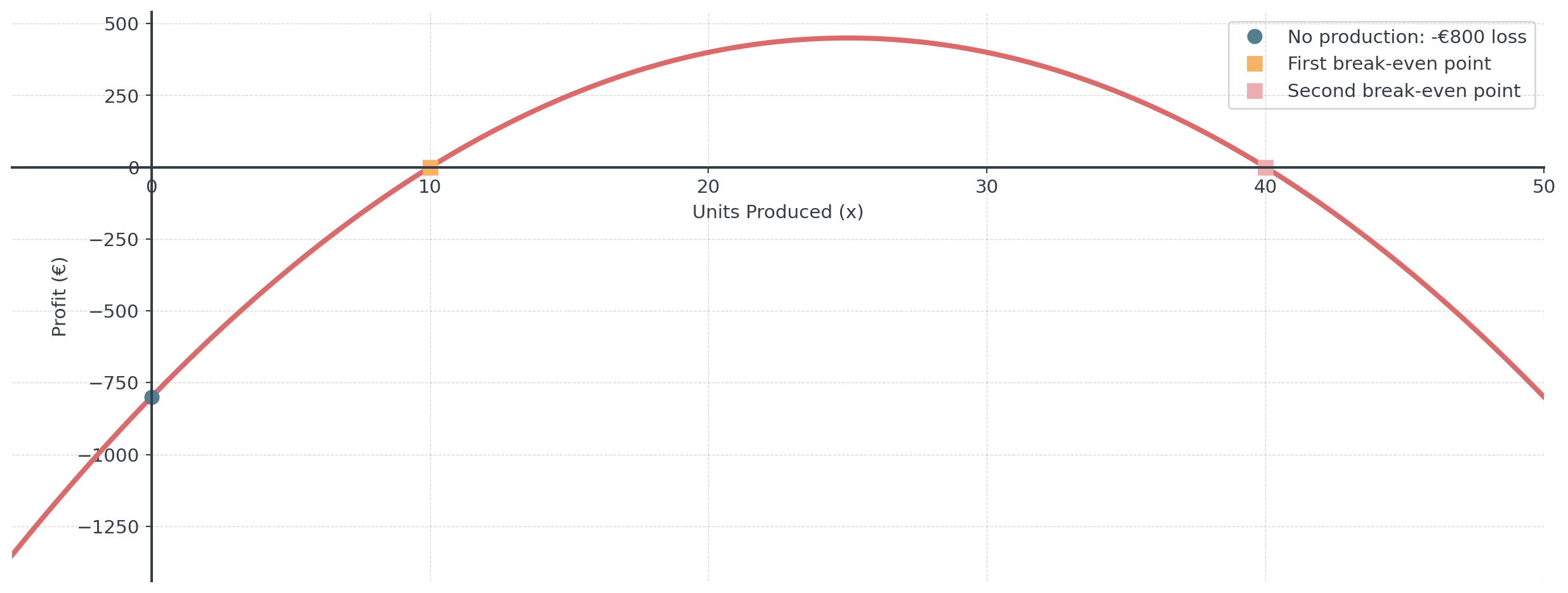
- A profit function is \(P(x) = -3x^2 + 240x - 3600\):
- Find the number of units that maximizes profit
- Calculate the maximum profit and the break-even points
- Convert \(f(x) = 2x^2 - 12x + 14\) to vertex form by completing the square, then identify the vertex.
Coffee Break - 15 Minutes
Projectile Motion
Product Launch Campaign
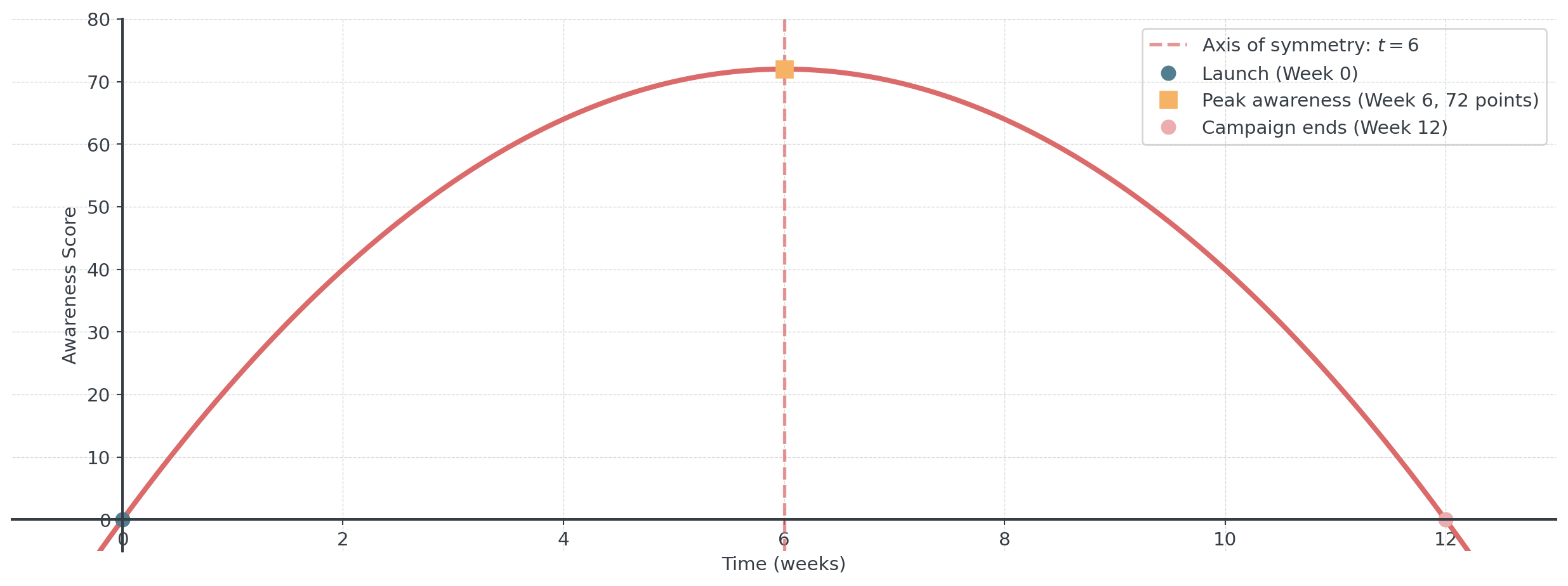
Marketing models new product awareness like projectile motion
\[A(t) = -2t^2 + 24t\] where \(A\) is awareness score and \(t\) is weeks after launch.
- Peak awareness time: \(t = -\frac{24}{2(-2)} = 6\) weeks
- Maximum awareness: \(A(6) = -72 + 144 = 72\) points
- Campaign ends when \(A(t) = 0\): at \(t = 0\) and \(t = 12\) weeks
. . .
Campaign follows symmetric pattern: builds to peak at 6 weeks, then decays at same rate.
Campaign Awareness
Area Optimization
Maximizing Area with Constraints
Classic problem: Maximum area with fixed perimeter
Rectangular Storage Area with 200 meters of fencing available. One side against a building (no fence) and we want to maximize storage area.
- Let \(x\) = width, \(y\) = length parallel to building
- Constraint: \(2x + y = 200\) (fencing)
- So: \(y = 200 - 2x\)
- Area: \(A = xy = x(200 - 2x) = 200x - 2x^2\)
- Maximum at: \(x = -\frac{200}{2(-2)} = 50\) meters
- Dimensions: 50m × 100m, Area = 5000 m²
Visualization
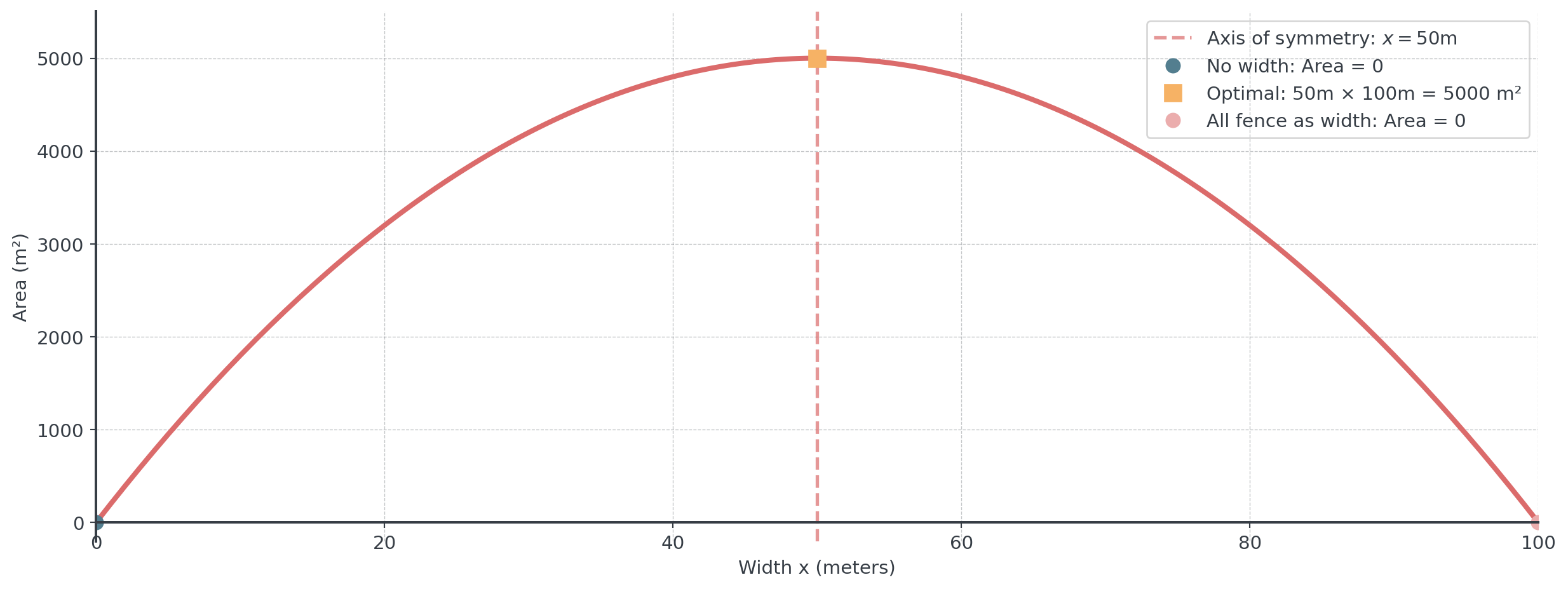
Symmetric design: Too narrow OR too wide both reduce area - optimal is exactly in the middle!
Collaborative Problem-Solving - 30 Minutes
Comprehensive Business Optimization
The Scenario: Smart Tech Product Launch
Smart Tech is launching a new tablet. Market research indicates:
- At €200: would sell 8,000 units per month
- At €400: would sell 4,000 units per month
- At €600: would sell 0 units (too expensive)
- Production cost: €150 per tablet
- Fixed monthly costs: €200,000
Assume linear demand relationship.
Your Tasks:
Work in groups of 3-4 students
Derive the demand function \(Q(p)\) where \(p\) is price
Express revenue \(R(p)\) as a function of price (this will be quadratic!)
Find the price that maximizes revenue
Express profit \(\Pi(p)\) as a function of price
Find the price that maximizes profit (different from revenue-maximizing price!)
If the company can only produce 5,000 tablets per month, should they use the profit-maximizing price? Explain.
Wrap-Up
Key Takeaways
- The vertex formula \(x = -\frac{b}{2a}\) is your optimization tool
- Quadratic functions model scenarios with changing rates
- Maximum/minimum depends on sign of \(a\)
- Revenue maximization ≠ Profit maximization
- Completing the square reveals the vertex form
- Real constraints may override mathematical optima
. . .
Every parabola has a minimum or a maximum point!
Final Assessment
5 minutes - Individual work
A small bakery’s daily profit for chocolate cakes is modeled by: \[P(x) = -x^2 + 14x - 33\] where \(x\) is the price in euros.
- Find the price that maximizes profit
- Calculate the maximum daily profit
- Find the break-even prices
Next Session Preview
Session 03-04: Transformations & Graphical Analysis
- Shifting functions horizontally and vertically
- Stretching and reflecting graphs
- Reading graphs to understand business scenarios
- Function composition in business contexts
- Multiple representation mastery
Homework Assignment: Complete Tasks 03-03!
