Session 03-03 - Quadratic Functions & Basic Optimization

Section 03: Functions as Business Models

Dr. Nikolai Heinrichs & Dr. Tobias Vlćek

Entry Quiz - 10 Minutes

Review from Session 03-02

Work individually, then we discuss together as group

Find the market equilibrium for:
- Demand: \(Q_d = 200 - 2p\)
- Supply: \(Q_s = 50 + 3p\)
Write the equation of a line passing through points (2, 8) and (5, 20).
For the cost function \(C(x) = 500 + 12x\) and revenue \(R(x) = 25x\), find the profit when \(x = 100\).

Homework Review - 20 Minutes

Discussing Tasks 03-02

Let’s discuss the most difficult tasks from last lecture

Problem 5: Market competition analysis
- How did you determine the break-even data usage?
Problem 6: Production planning with constraints
- Challenges with multiple constraints?
Problem 7: Dynamic pricing (if attempted)
- What price seemed optimal in your testing?

Today we’ll learn the exact method to find that optimal price!

Introduction to Quadratic Functions

From Linear to Quadratic

Quadratic functions model accelerating change

Linear vs. Quadratic:

Linear: \(f(x) = mx + b\) → Constant rate of change
Quadratic: \(f(x) = ax^2 + bx + c\) → Changing rate of change
Graph shape: Quadratic → Parabola (U-shaped or ∩-shaped)
Business meaning:
- Linear → Fixed relationships
- Quadratic → Optimization opportunities!

Standard Form

The foundation: f(x) = ax² + bx + c

Key components:

a: Direction and width
- \(a > 0\): Opens upward (has minimum)
- \(a < 0\): Opens downward (has maximum)
- \(|a|\) larger → Narrower parabola
b: Affects position of vertex
c: y-intercept (value when \(x = 0\))

Example: Profit Function

Quadratic Profit Function: \(P(x) = -2x^2 + 100x - 800\)

Quick Practice - 10 Minutes

Work individually, then we discuss

Determine: Does it open upward (U) or downward (∩)?
Determine: Does it have a maximum or minimum?
Determine: What is the y-intercept?

\(R(x) = -3x^2 + 120x - 500\)
\(C(x) = 2x^2 + 40x + 1000\)
\(P(x) = -x^2 + 50x - 300\)

Challenge: For c. find the break-even points.

Break - 10 Minutes

Finding the Vertex

The Vertex Formula

The key: x = -b/2a

For \(f(x) = ax^2 + bx + c\):

Vertex x-coordinate: \(x_v = -\frac{b}{2a}\)
Vertex y-coordinate: \(f(x_v) = f(-\frac{b}{2a})\)
Vertex represents:
- Maximum if \(a < 0\) (parabola opens down)
- Minimum if \(a > 0\) (parabola opens up)
Axis of symmetry: Vertical line \(x = x_v\)

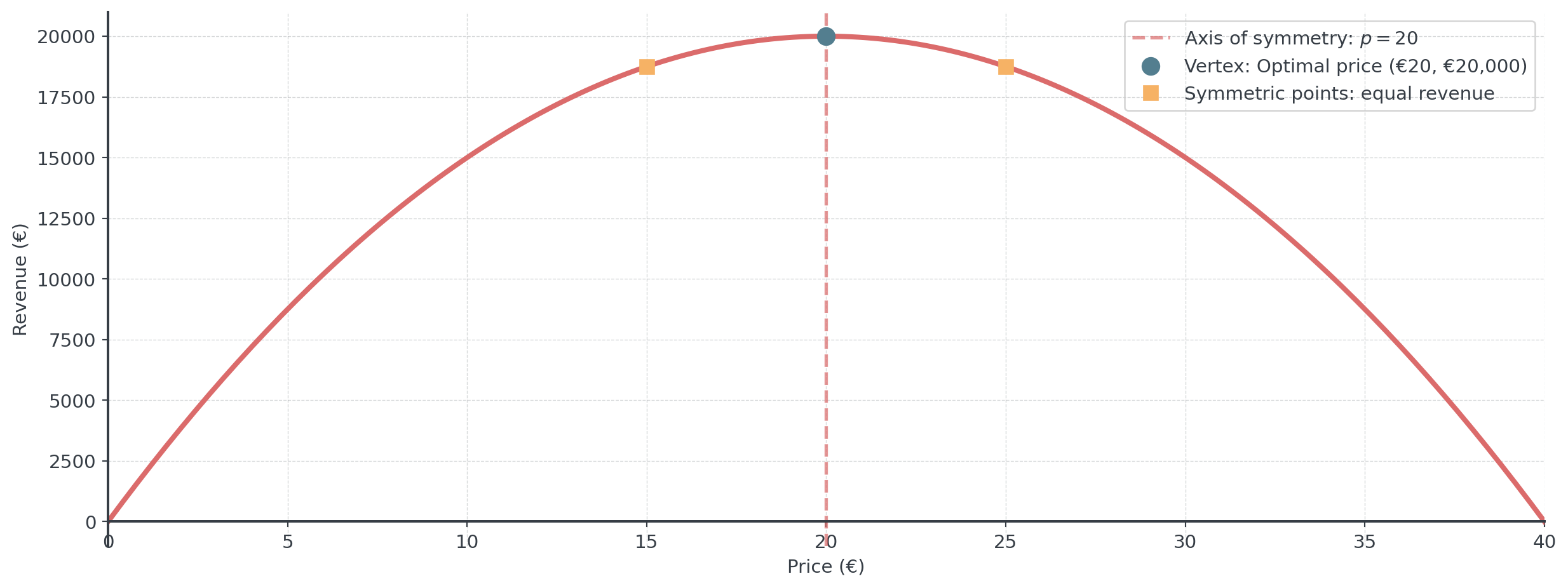
Vertex Example: Revenue Optimization

A company’s revenue depends on price:

\[R(p) = -50p^2 + 2000p\]

Find optimal price: \(p_v = -\frac{2000}{2(-50)} = -\frac{2000}{-100} = 20\) euros
Maximum revenue: \(R(20) = 20000\) euros
Interpretation: Charging €20 maximizes revenue at €20,000

The axis of symmetry divides the parabola into mirror images. Points equidistant from it have equal revenue!

Visualization

\(R(p) = -50p^2 + 2000p\) with Vertex and Axis of Symmetry

Vertex Form

Alternative representation: f(x) = a(x - h)² + k

Vertex: \((h, k)\) - directly visible!
Direction: \(a\) (same as standard form)
Advantage: Vertex immediately apparent
Transformation from vertex:
- Horizontal shift by \(h\)
- Vertical shift by \(k\)
Example: \(f(x) = 2(x - 3)^2 + 5\) → Vertex at \((3, 5)\), minimum
Example: \(g(x) = -(x + 4)^2 + 10\) → Vertex at \((-4, 10)\), maximum

Completing the Square

Converting to Vertex Form

Transform \(f(x) = ax^2 + bx + c\) to \(f(x) = a(x - h)^2 + k\)

Process:

Factor out \(a\) from first two terms
Complete the square inside parentheses
Simplify to vertex form

Sorry, I know I said we don’t need that!

Step-by-Step Example

Convert \(f(x) = 2x^2 - 12x + 10\) to vertex form

Factor out 2: \(f(x) = 2(x^2 - 6x) + 10\)
Complete square: Need \((\frac{-6}{2})^2 = 9\)
Add and subtract: \(f(x) = 2(x^2 - 6x + 9 - 9) + 10\)
Rewrite: \(f(x) = 2((x - 3)^2 - 9) + 10\)
Distribute: \(f(x) = 2(x - 3)^2 - 18 + 10\)
Final form: \(f(x) = 2(x - 3)^2 - 8\)
Vertex: \((3, -8)\) with minimum value -8

Fast Exercise

Solve in 5 minutes, then we compare solutions

Convert \(f(x) = 3x^2 + 18x + 20\) to vertex form by completing the square.

Business Applications

Price-Dependent Demand

When price affects quantity: Revenue becomes quadratic!

Basic Scenario:

Demand function: \(Q = a - bp\) (quantity depends on price)
Revenue: \(R = p \times Q = p(a - bp)\)
Expanded: \(R(p) = ap - bp^2 = -bp^2 + ap\)
This is quadratic in \(p\)!

Remember, we have seen this in the past!

Example: Concert Venue

A venue (capacity: 1000) has ticket demand: \(Q = 1000 - 20p\)

Revenue function: \(R(p) = p(1000 - 20p) = 1000p - 20p^2\)
Optimal price: \(p^* = -\frac{1000}{2(-20)} = \frac{1000}{40} = 25\) euros
Tickets sold: \(Q = 1000 - 20(25) = 500\)
Maximum revenue: \(R(25) = 25 \times 500 = 12,500\)
At €0: Demand = 1000 (full capacity if free)
At €50: Demand = 0 (too expensive, no one buys)

Note: This maximizes revenue, not necessarily profit!

Guided Practice - 20 Minutes

Individual Exercise Block

Work alone for 15 minutes, then we compare solutions

For \(f(x) = x^2 - 8x + 12\):
1. Find the vertex using the formula
2. Determine if it’s a maximum or minimum and find the y-intercept
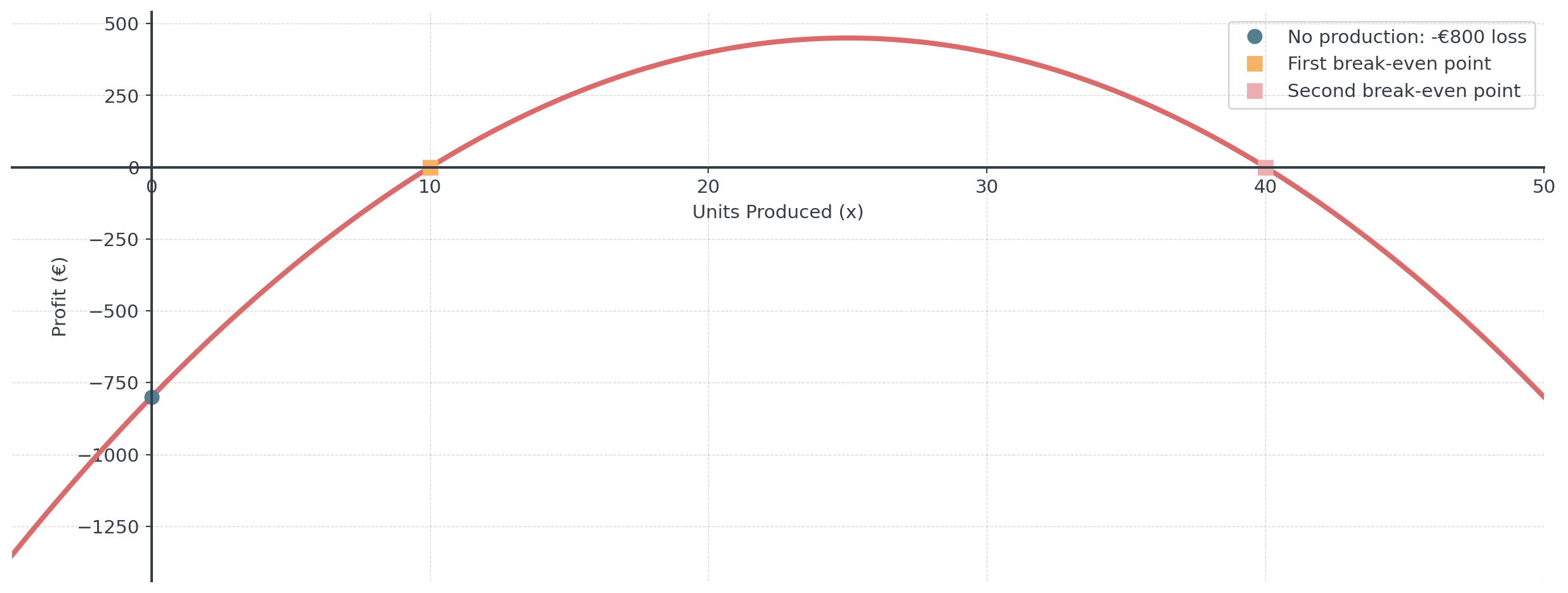
A profit function is \(P(x) = -3x^2 + 240x - 3600\):
1. Find the number of units that maximizes profit
2. Calculate the maximum profit and the break-even points
Convert \(f(x) = 2x^2 - 12x + 14\) to vertex form by completing the square, then identify the vertex.

Coffee Break - 15 Minutes

Projectile Motion

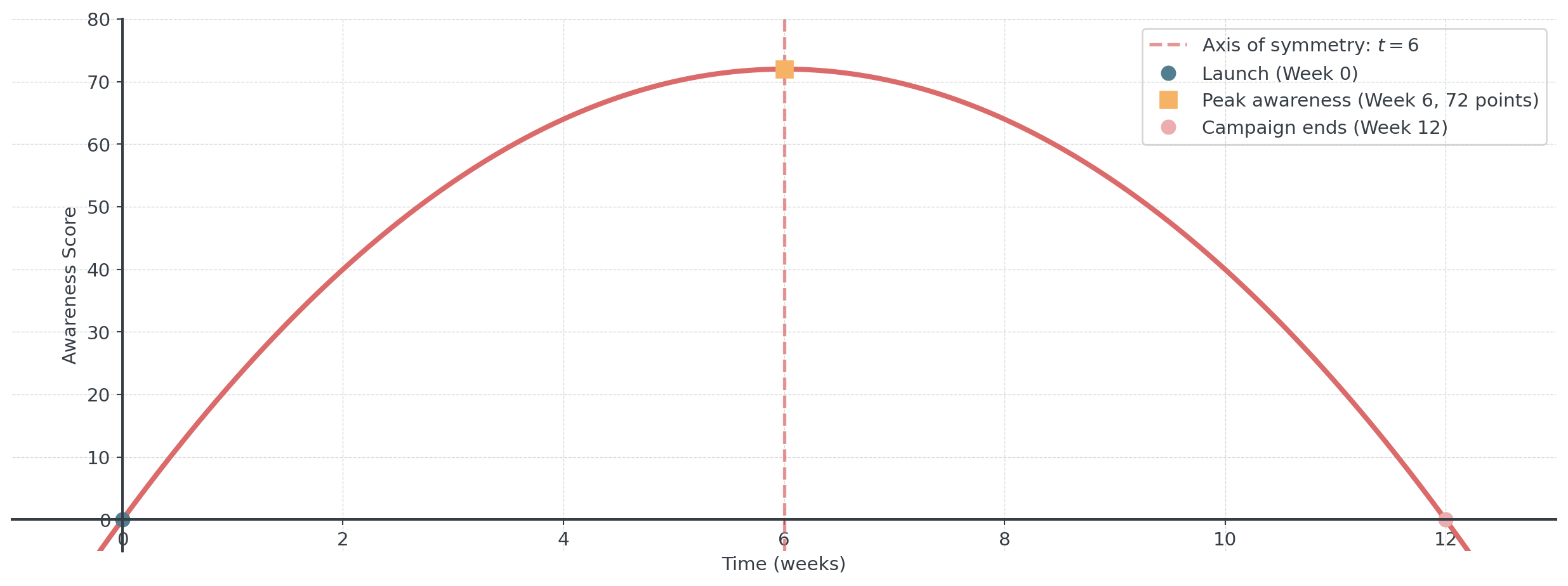
Product Launch Campaign

Marketing models new product awareness like projectile motion

\[A(t) = -2t^2 + 24t\] where \(A\) is awareness score and \(t\) is weeks after launch.

Peak awareness time: \(t = -\frac{24}{2(-2)} = 6\) weeks
Maximum awareness: \(A(6) = -72 + 144 = 72\) points
Campaign ends when \(A(t) = 0\): at \(t = 0\) and \(t = 12\) weeks

Campaign follows symmetric pattern: builds to peak at 6 weeks, then decays at same rate.

Campaign Awareness

Product Launch Campaign: \(A(t) = -2t^2 + 24t\)

Area Optimization

Maximizing Area with Constraints

Classic problem: Maximum area with fixed perimeter

Rectangular Storage Area with 200 meters of fencing available. One side against a building (no fence) and we want to maximize storage area.

Let \(x\) = width, \(y\) = length parallel to building
Constraint: \(2x + y = 200\) (fencing)
So: \(y = 200 - 2x\)
Area: \(A = xy = x(200 - 2x) = 200x - 2x^2\)
Maximum at: \(x = -\frac{200}{2(-2)} = 50\) meters
Dimensions: 50m × 100m, Area = 5000 m²

Visualization

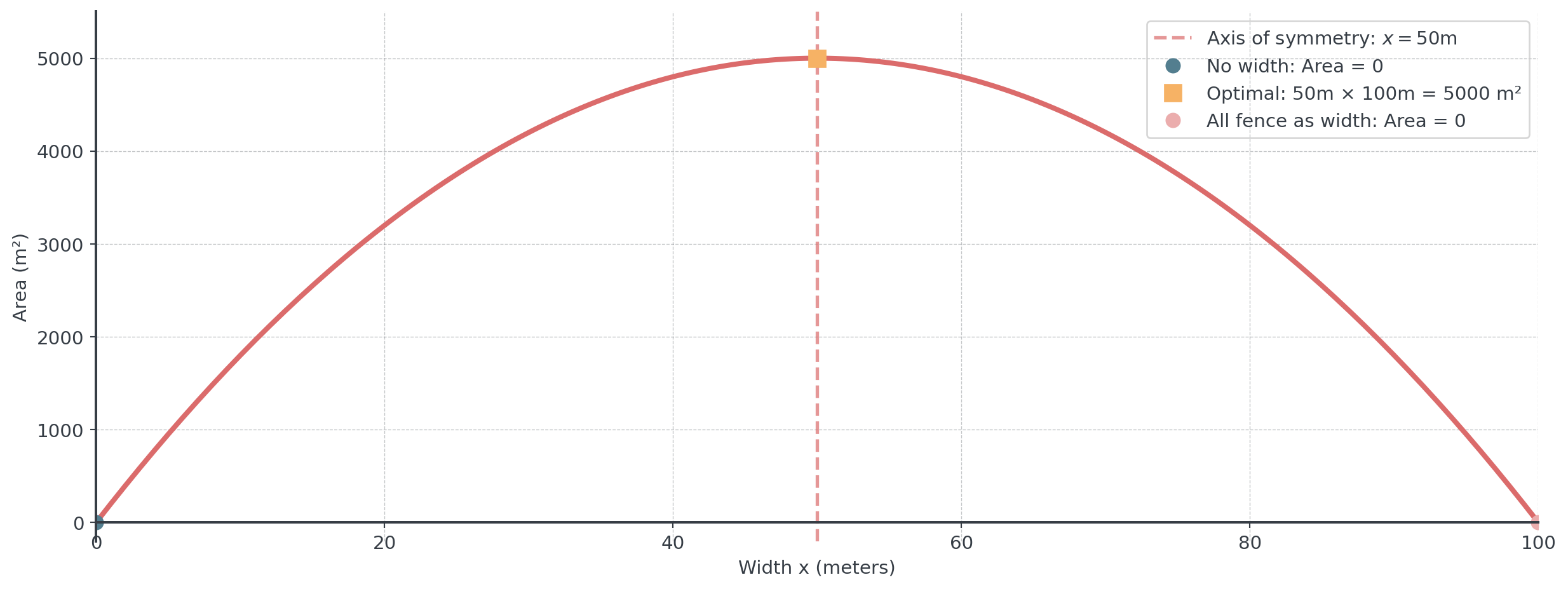
Symmetric design: Too narrow OR too wide both reduce area - optimal is exactly in the middle!

Collaborative Problem-Solving - 30 Minutes

Comprehensive Business Optimization

The Scenario: Smart Tech Product Launch

Smart Tech is launching a new tablet. Market research indicates:

At €200: would sell 8,000 units per month
At €400: would sell 4,000 units per month
At €600: would sell 0 units (too expensive)
Production cost: €150 per tablet
Fixed monthly costs: €200,000

Assume linear demand relationship.

Your Tasks:

Work in groups of 3-4 students

Derive the demand function \(Q(p)\) where \(p\) is price
Express revenue \(R(p)\) as a function of price (this will be quadratic!)
Find the price that maximizes revenue
Express profit \(\Pi(p)\) as a function of price
Find the price that maximizes profit (different from revenue-maximizing price!)
If the company can only produce 5,000 tablets per month, should they use the profit-maximizing price? Explain.

Wrap-Up

Key Takeaways

The vertex formula \(x = -\frac{b}{2a}\) is your optimization tool
Quadratic functions model scenarios with changing rates
Maximum/minimum depends on sign of \(a\)
Revenue maximization ≠ Profit maximization
Completing the square reveals the vertex form
Real constraints may override mathematical optima

Remember

Every parabola has a minimum or a maximum point!

Final Assessment

5 minutes - Individual work

A small bakery’s daily profit for chocolate cakes is modeled by: \[P(x) = -x^2 + 14x - 33\] where \(x\) is the price in euros.

Find the price that maximizes profit
Calculate the maximum daily profit
Find the break-even prices

Next Session Preview

Session 03-04: Transformations & Graphical Analysis

Shifting functions horizontally and vertically
Stretching and reflecting graphs
Reading graphs to understand business scenarios
Function composition in business contexts
Multiple representation mastery

Homework Assignment: Complete Tasks 03-03!