Tasks: Graphical Calculus Mastery

Session 05-05 Practice Problems

EXAM: This type of problem appears on EVERY exam. Master these skills!

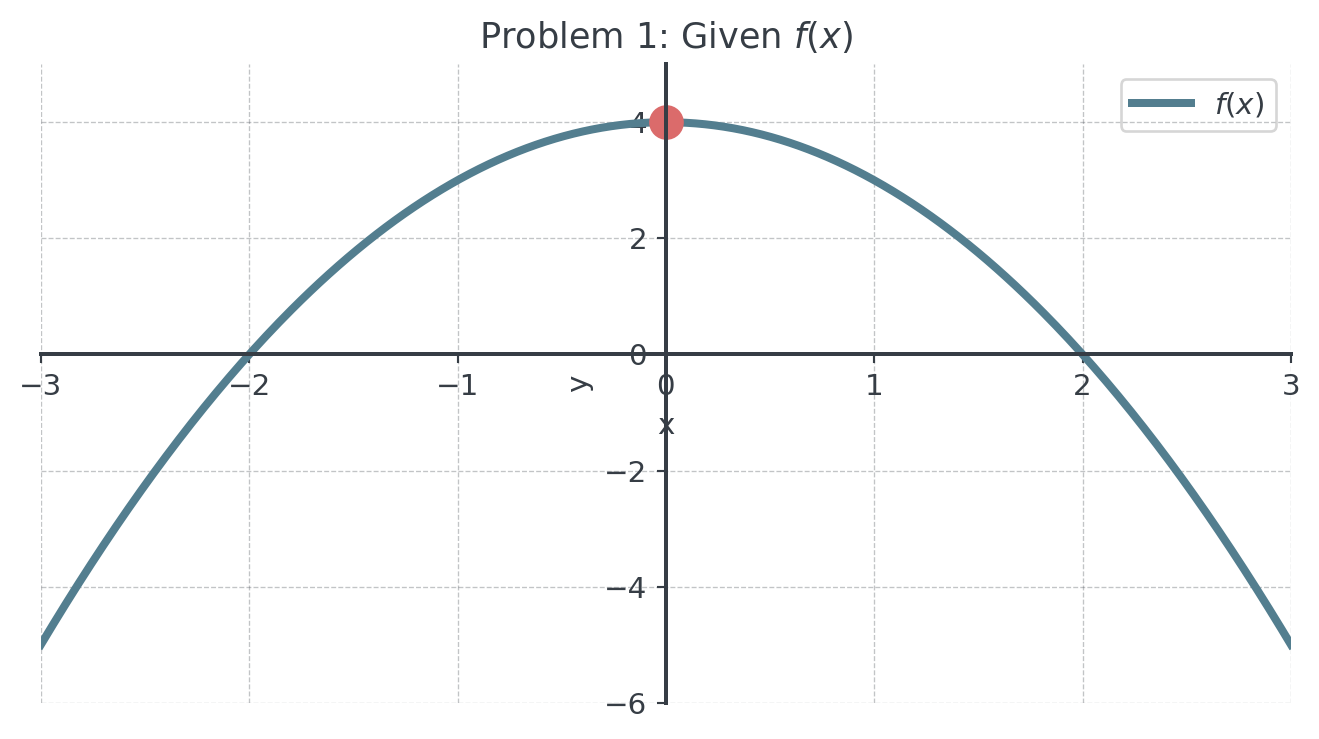
1 Problem 1: Polynomial Function (x)

Given the graph of \(f(x)\) below, sketch the graph of \(f'(x)\).

Solution

Analysis:

\(f\) increasing for \(x < 0\) → \(f' > 0\)
\(f\) has maximum at \(x = 0\) → \(f' = 0\)
\(f\) decreasing for \(x > 0\) → \(f' < 0\)
\(f\) is concave down everywhere → \(f'\) is decreasing

Graph of \(f'(x)\):

The graph shows f’(x) = -2x as a straight line passing through the origin with negative slope. The region above the x-axis (for x < 0) is shaded to indicate where f is increasing, and the region below the x-axis (for x > 0) is shaded to indicate where f is decreasing. The zero at x = 0 corresponds to the maximum of f.

Key points:

\(f'(x) > 0\) for \(x < 0\) (positive region)
\(f'(0) = 0\) (zero at maximum)
\(f'(x) < 0\) for \(x > 0\) (negative region)
\(f'\) is linear and decreasing

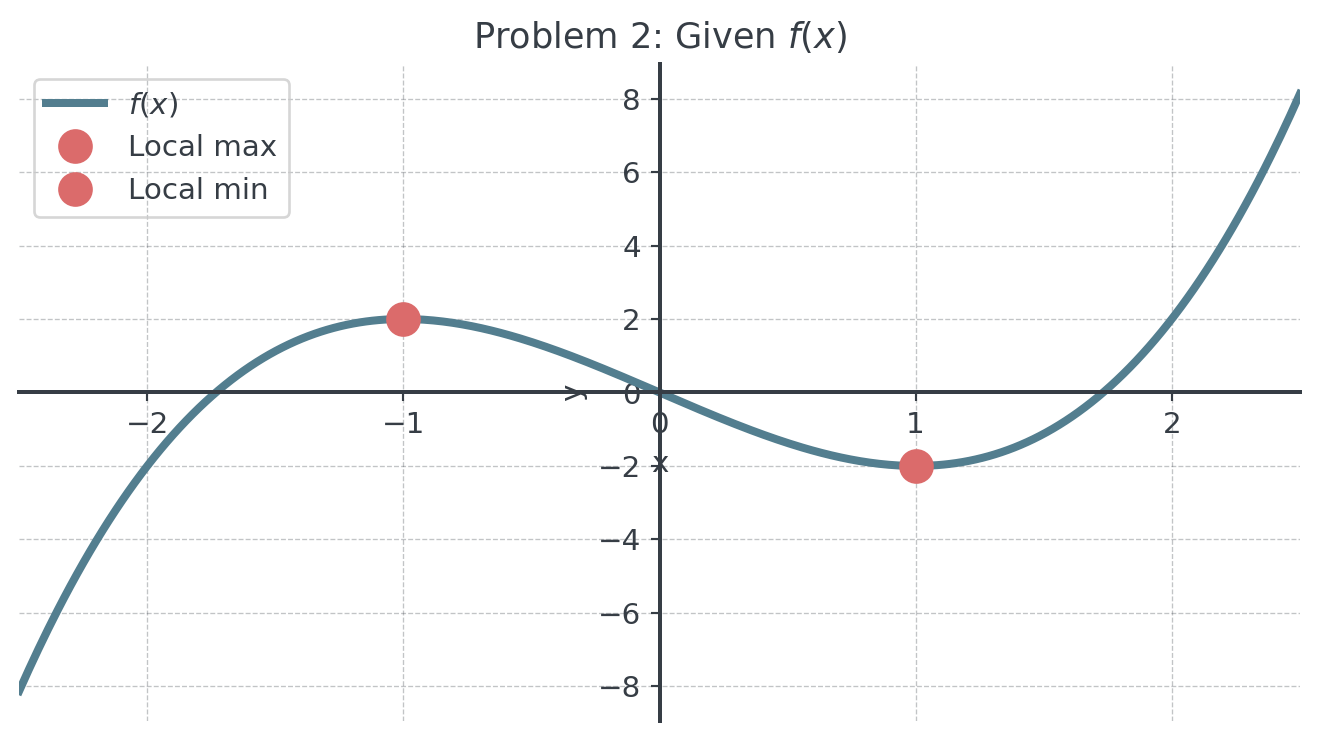
2 Problem 2: Cubic Function (x)

Given the graph of \(f(x)\), sketch \(f'(x)\) and identify all critical points.

Solution

Analysis:

\(f\) increasing on \((-\infty, -1)\) → \(f' > 0\)
Local max at \(x = -1\) → \(f'(-1) = 0\)
\(f\) decreasing on \((-1, 1)\) → \(f' < 0\)
Local min at \(x = 1\) → \(f'(1) = 0\)
\(f\) increasing on \((1, \infty)\) → \(f' > 0\)
\(f\) concave down then concave up → \(f'\) has a minimum

Graph of \(f'(x)\):

The graph shows f’(x) = 3x^2 - 3, an upward-opening parabola with zeros at x = -1 and x = 1. The region below the x-axis (between x = -1 and x = 1) is shaded, indicating where f is decreasing. The regions above the x-axis (for |x| > 1) are shaded differently, showing where f is increasing.

Critical points:

\(x = -1\): Local maximum (f’ changes + to -)
\(x = 1\): Local minimum (f’ changes - to +)

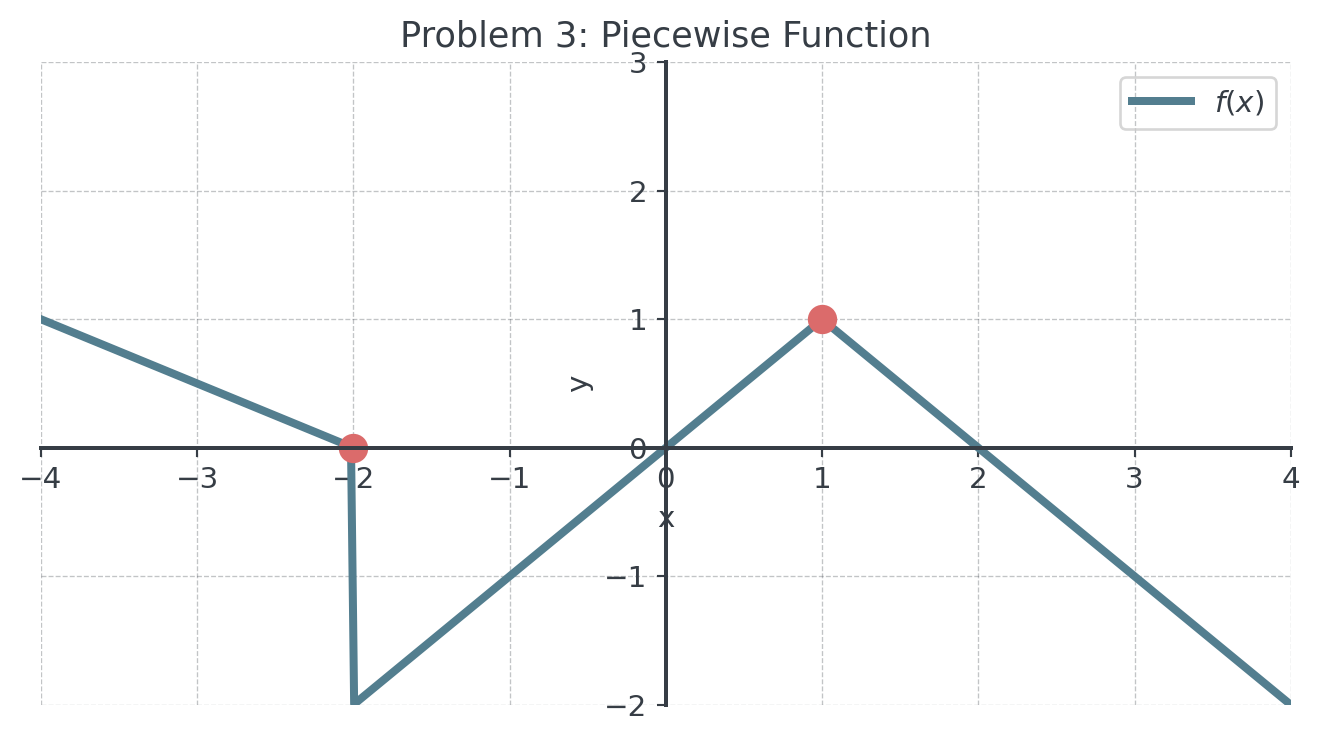
3 Problem 3: Piecewise Linear Function (xx)

Sketch \(f'(x)\) for the piecewise linear function shown. Where does \(f'(x)\) not exist?

Solution

Analysis:

For \(x < -2\): slope is \(-0.5\)
For \(-2 < x < 1\): slope is \(1\)
For \(x > 1\): slope is \(-1\)
At \(x = -2\) and \(x = 1\): corners → \(f'\) does not exist

Graph of \(f'(x)\) (step function):

The graph shows f’(x) as a step function with three constant segments: f’(x) = -0.5 for x < -2, f’(x) = 1 for -2 < x < 1, and f’(x) = -1 for x > 1. Open and filled circles at x = -2 and x = 1 indicate the jump discontinuities where the derivative does not exist (corresponding to corners in f).

\(f'\) does not exist at: \(x = -2\) and \(x = 1\) (corners in \(f\))

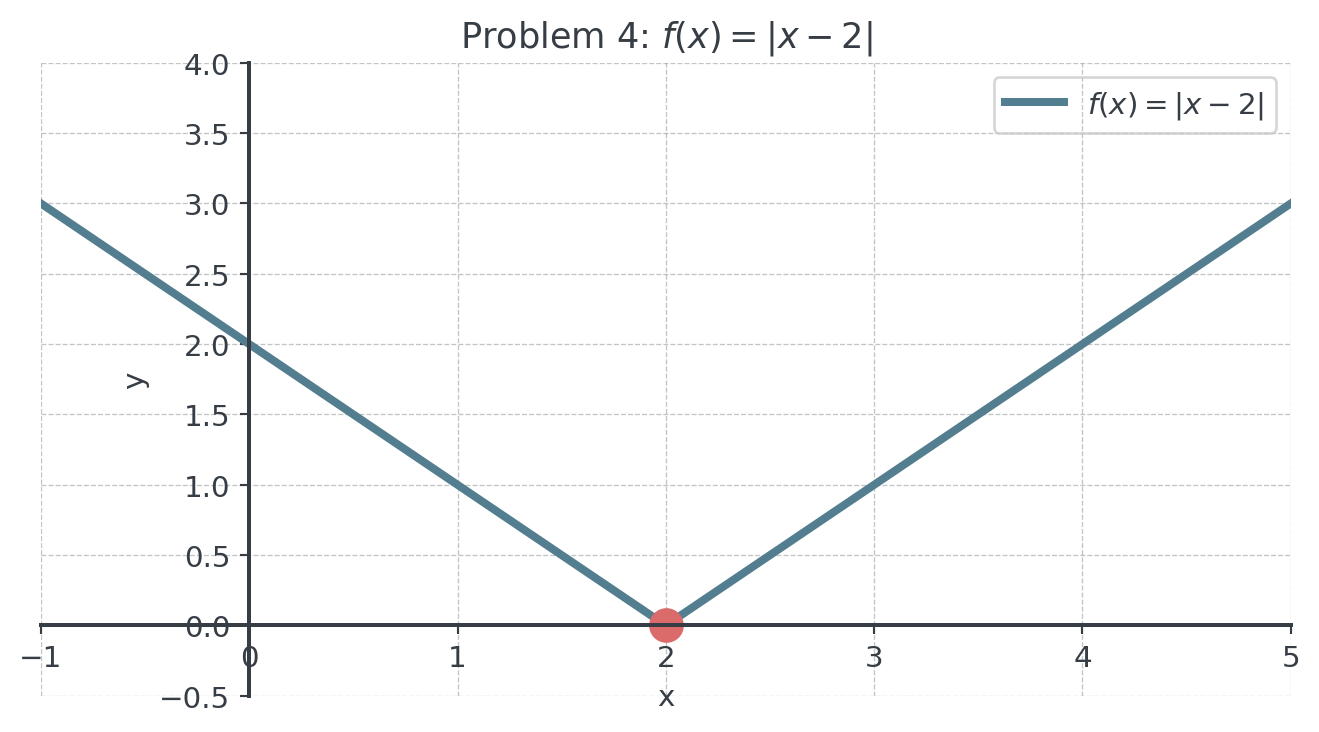
4 Problem 4: Absolute Value Function (xx)

Sketch \(f'(x)\) for \(f(x) = |x - 2|\) on the interval \([-1, 5]\).

Solution

Analysis:

For \(x < 2\): \(f(x) = -(x-2) = 2-x\), so slope is \(-1\)
For \(x > 2\): \(f(x) = x-2\), so slope is \(1\)
At \(x = 2\): sharp corner → \(f'(2)\) does not exist

Graph of \(f'(x)\):

The graph shows f’(x) as two horizontal segments: f’(x) = -1 for x < 2 and f’(x) = 1 for x > 2. Open circles at (2, -1) and (2, 1) indicate the jump discontinuity. A dashed vertical line at x = 2 marks where f’(x) does not exist (DNE), corresponding to the sharp corner in the absolute value function.

Note: \(f'(x) = -1\) for \(x < 2\), \(f'(x) = 1\) for \(x > 2\), and \(f'(2)\) does not exist.

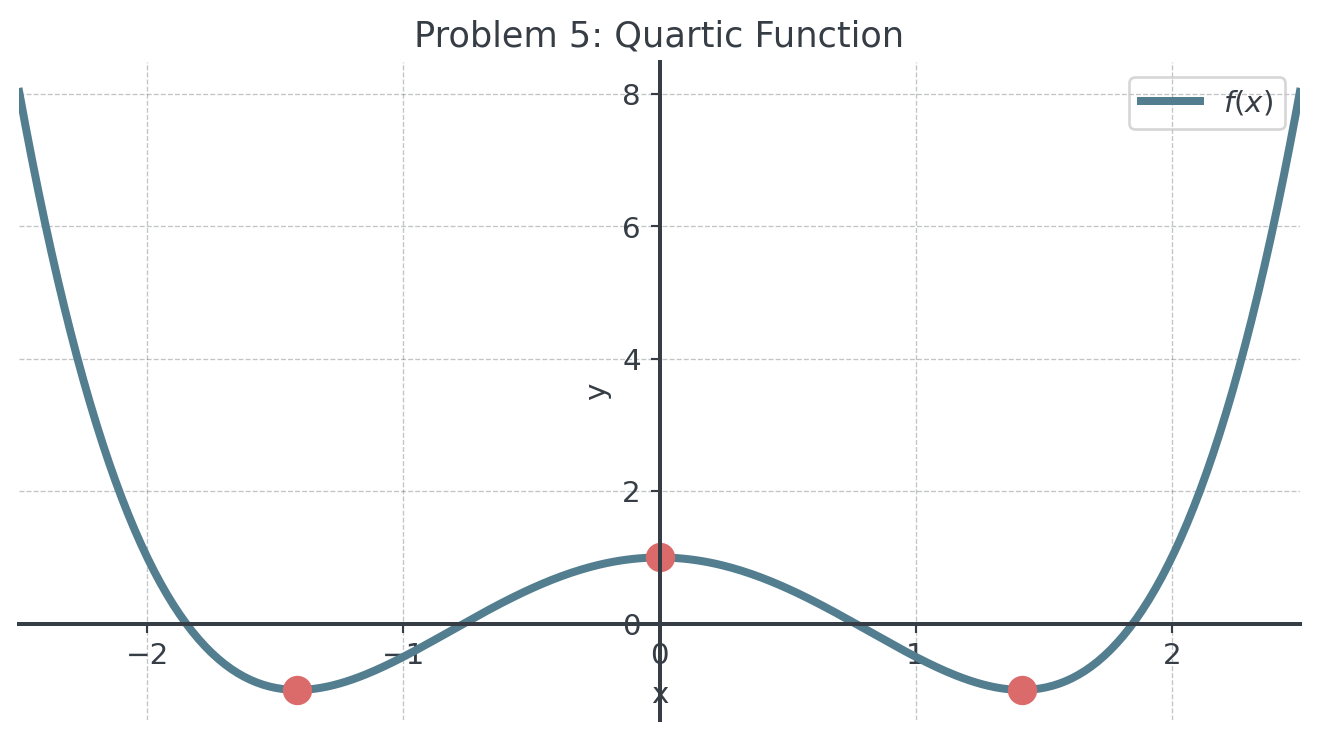
5 Problem 5: Quartic with Multiple Extrema (xxx)

Sketch \(f'(x)\) and \(f''(x)\) for the quartic function shown.

Quartic function with two minima and one maximum

Solution

Analysis:

\(f\) has local minima at \(x = \pm\sqrt{2}\)
\(f\) has local maximum at \(x = 0\)
Critical points: \(x = -\sqrt{2}, 0, \sqrt{2}\)

Graphs of \(f'(x)\) and \(f''(x)\):

Two side-by-side graphs are shown. Left: f’(x) = 2x^3 - 4x is a cubic curve with three zeros at x = -sqrt(2), 0, and sqrt(2), corresponding to the three critical points of f. Right: f’‘(x) = 6x^2 - 4 is an upward-opening parabola with zeros at x = plus/minus sqrt(2/3), marking the inflection points of f. Shaded regions indicate where f is concave up (f’’ > 0) and concave down (f’’ < 0).

Key observations:

\(f'\) has three zeros (corresponding to the three critical points of \(f\))
\(f''\) has two zeros at \(x = \pm\sqrt{2/3}\) (inflection points of \(f\))
\(f\) is concave up on \((-\infty, -\sqrt{2/3}) \cup (\sqrt{2/3}, \infty)\)
\(f\) is concave down on \((-\sqrt{2/3}, \sqrt{2/3})\)

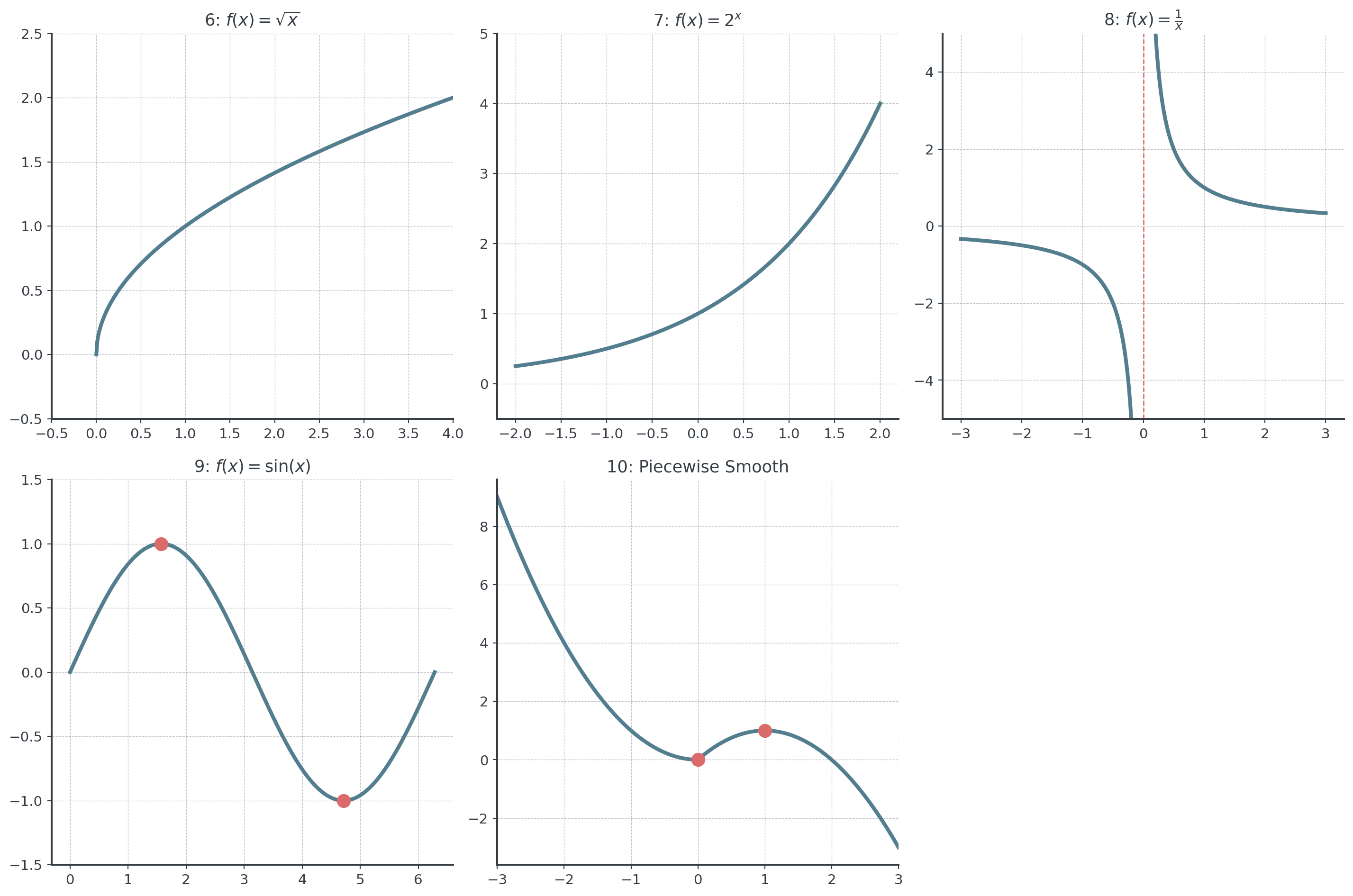
6 Problems 6-10: Quick Sketches (x)

For each function graph below, sketch \(f'(x)\). Identify critical points.

Solution

Problem 6: \(f'(x) = \frac{1}{2\sqrt{x}}\)

Always positive (always increasing)
Decreasing slope (concave down)
\(f'(0)\) does not exist (vertical tangent)

Problem 7: \(f'(x) = 2^x \ln(2)\)

Always positive (always increasing)
Increasing slope (concave up)
No critical points

Problem 8: \(f'(x) = -\frac{1}{x^2}\)

Always negative (always decreasing)
No critical points
\(f'(0)\) does not exist (vertical asymptote)

Problem 9: \(f'(x) = \cos(x)\)

\(f'(\pi/2) = 0\) (local max)
\(f'(3\pi/2) = 0\) (local min)
\(f'\) oscillates between \(-1\) and \(1\)

Problem 10:

For \(x < 0\): \(f'(x) = 2x\) (increasing from negative to 0)
For \(x > 0\): \(f'(x) = -2x + 2\) (decreasing from 2 to negative)
At \(x = 0\): \(f'(0) = 0\) (critical point, but not smooth - corner)
At \(x = 1\): \(f'(1) = 0\) (local maximum)

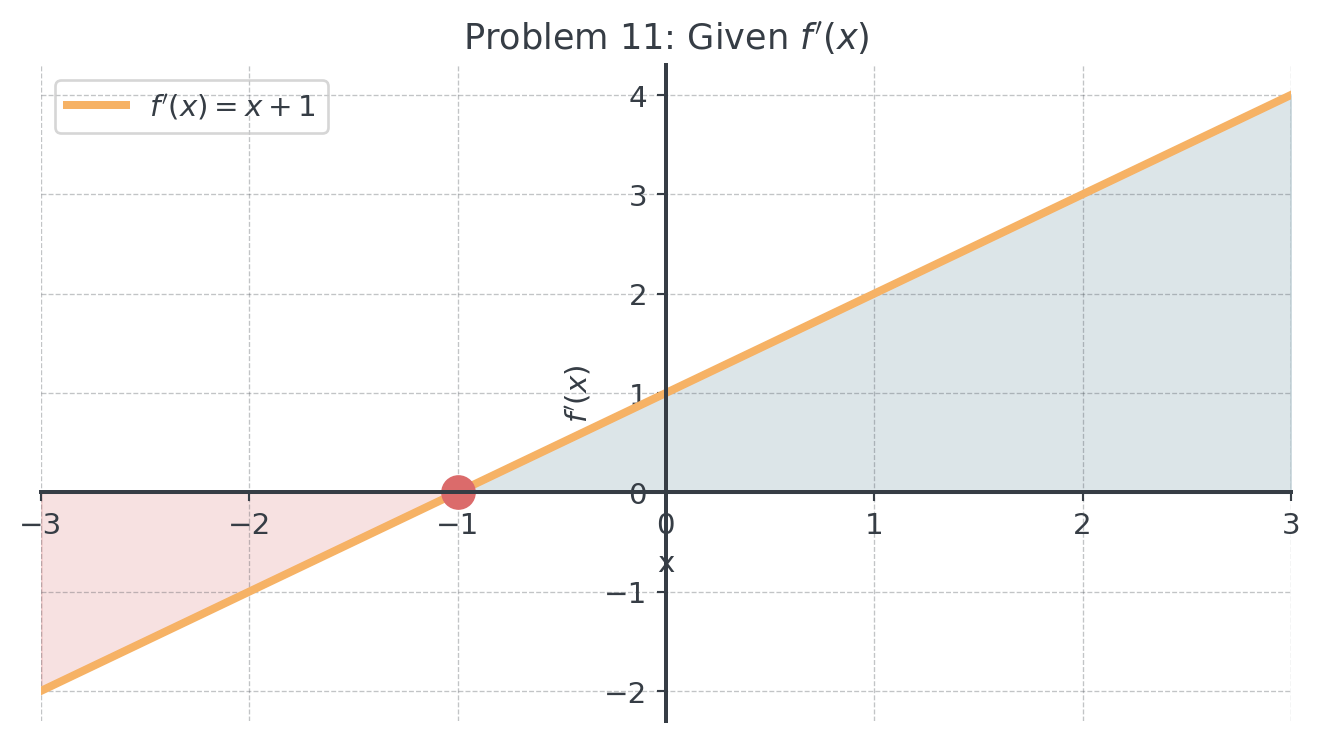
7 Problem 11: Linear Derivative (x)

Given the graph of \(f'(x)\) below:

Where is \(f(x)\) increasing? Decreasing?
Where does \(f(x)\) have local extrema? Classify them.
Sketch a possible graph of \(f(x)\).

Solution

Increasing/Decreasing:
- \(f\) decreasing on \((-\infty, -1)\) where \(f' < 0\)
- \(f\) increasing on \((-1, \infty)\) where \(f' > 0\)
Local extrema:
- \(x = -1\): Local minimum (f’ changes from negative to positive)
Possible graph of \(f(x)\):

The graph shows a possible f(x) = x^2/2 + x + C as an upward-opening parabola with a local minimum at x = -1, marked with a point. The curve decreases for x < -1 (where f’ < 0) and increases for x > -1 (where f’ > 0).

Note: The vertical position is not unique - we can add any constant \(C\).

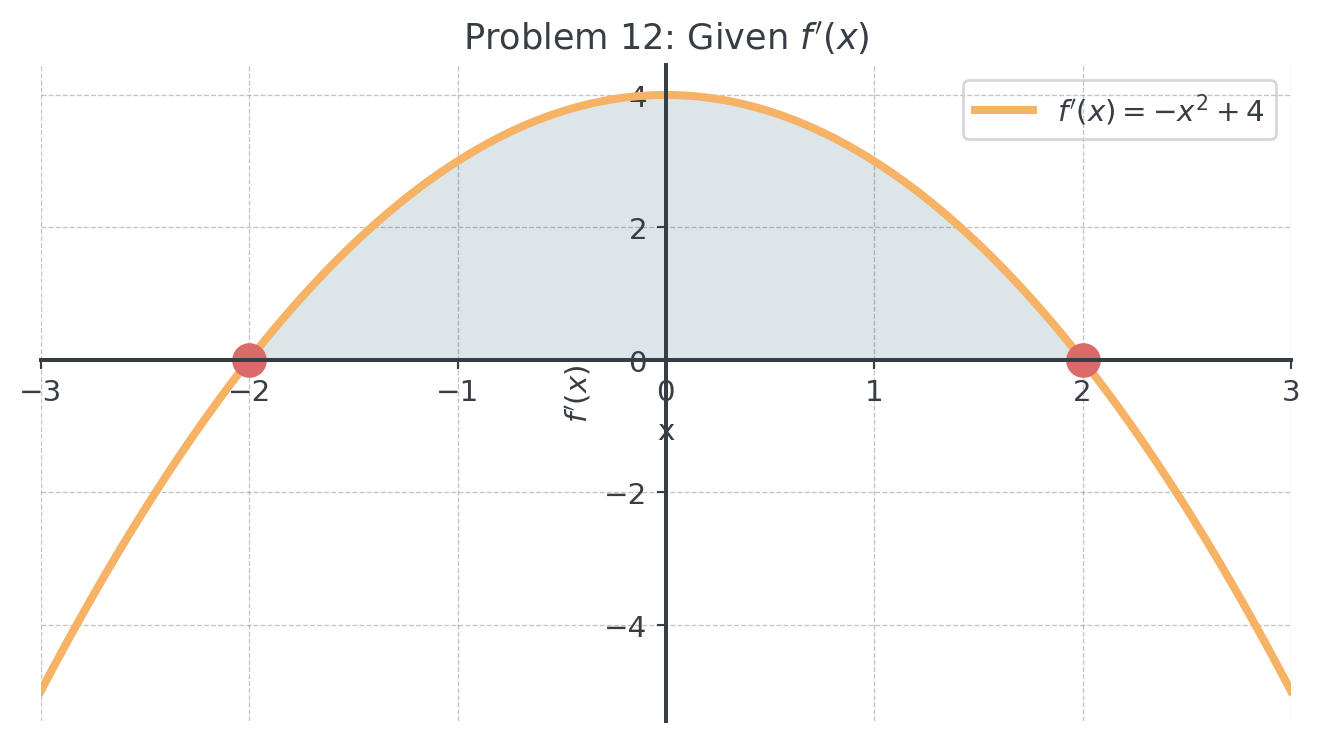
8 Problem 12: Quadratic Derivative (xx)

Given \(f'(x)\) shown below:

Find all critical points of \(f(x)\) and classify them.
Where is \(f(x)\) concave up? Concave down?
Sketch \(f(x)\).

Solution

Critical points:
- \(x = -2\): Local minimum (\(f'\) changes - to +)
- \(x = 2\): Local maximum (\(f'\) changes + to -)
Concavity:
- \(f''(x) = (f')'(x) = -2x\)
- \(f\) concave up where \(f'' > 0\): \(x < 0\)
- \(f\) concave down where \(f'' < 0\): \(x > 0\)
- Inflection point at \(x = 0\) (where \(f'\) has maximum)
Sketch of \(f(x)\):

The graph shows a possible f(x) = -x^3/3 + 4x as a cubic curve with a local minimum at x = -2, a local maximum at x = 2, and an inflection point at x = 0 (marked with a square). The curve changes concavity at the inflection point, transitioning from concave up to concave down.

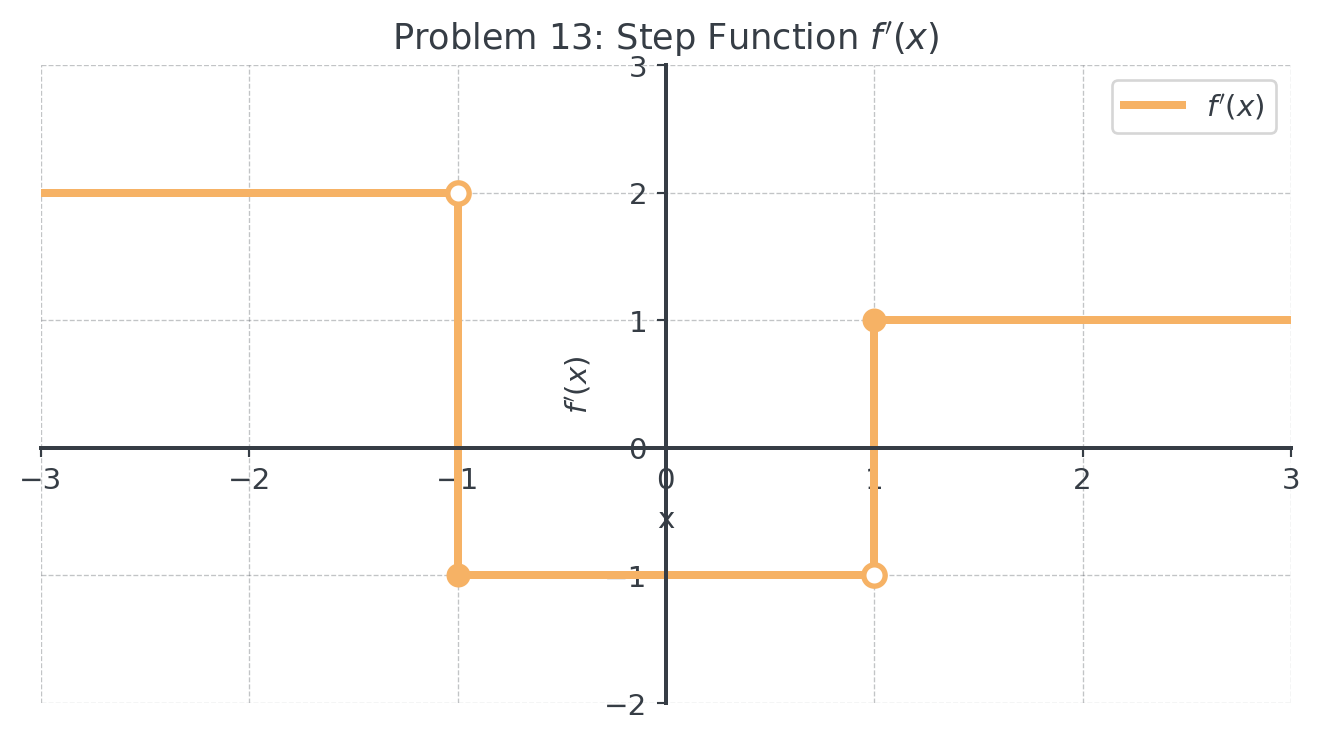
9 Problem 13: Piecewise Constant Derivative (xx)

Given the step function \(f'(x)\) below, sketch \(f(x)\).

Solution

Analysis:

For \(x < -1\): \(f'(x) = 2\) → \(f\) increasing with slope 2
For \(-1 < x < 1\): \(f'(x) = -1\) → \(f\) decreasing with slope -1
For \(x > 1\): \(f'(x) = 1\) → \(f\) increasing with slope 1
At \(x = -1, 1\): \(f'\) jumps → corners in \(f\)

Sketch of \(f(x)\):

The graph shows a possible f(x) as a piecewise linear function with three segments: slope 2 for x < -1, slope -1 for -1 < x < 1, and slope 1 for x > 1. Corners are marked at x = -1 (local maximum) and x = 1 (local minimum), where the derivative is discontinuous.

Key features:

\(f\) is piecewise linear (straight line segments)
Corners at \(x = -1\) and \(x = 1\)
Local maximum at \(x = -1\)
Local minimum at \(x = 1\)

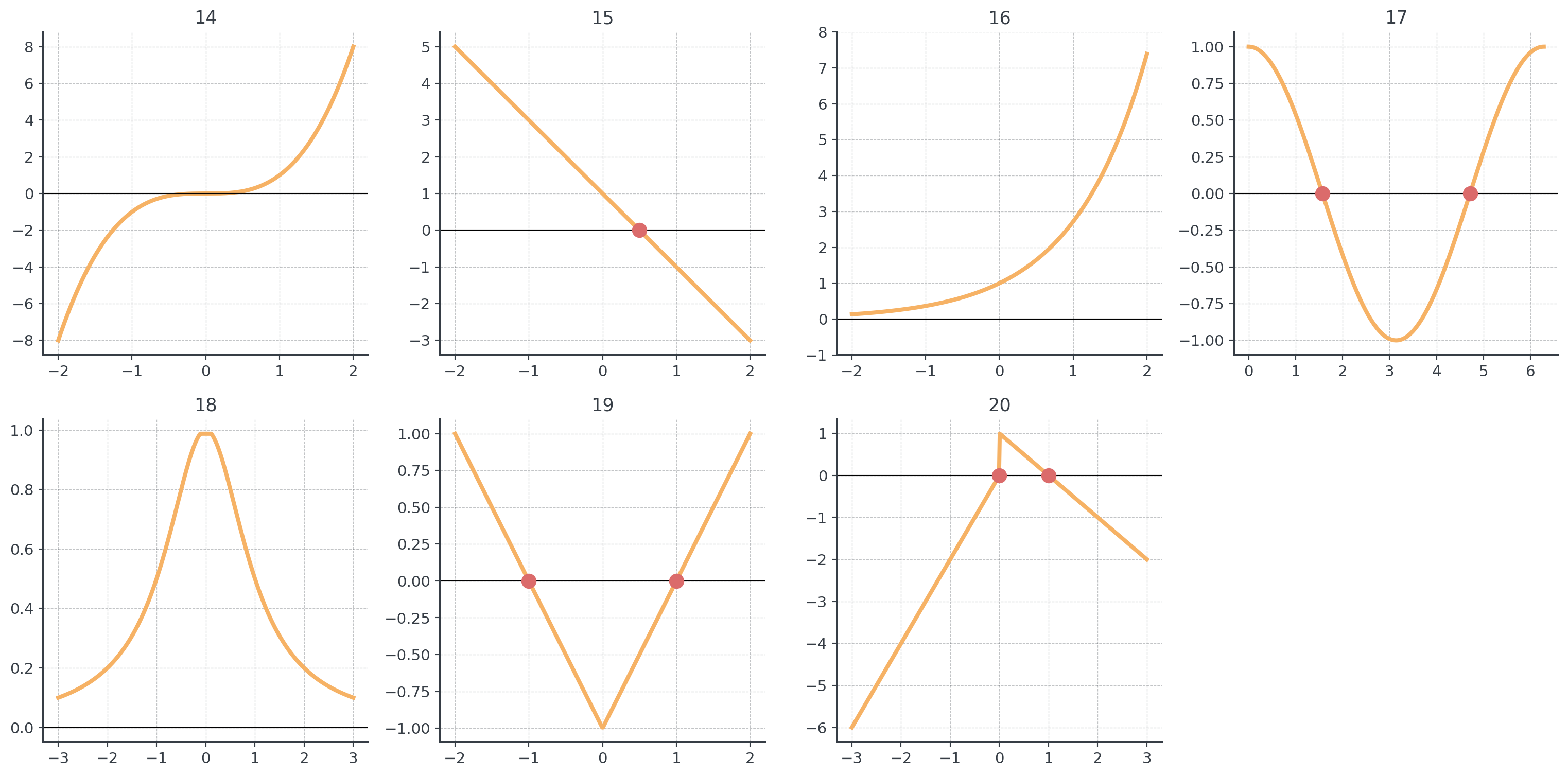
10 Problems 14-20: Quick Analysis (xx)

For each derivative graph, answer: Where is \(f\) increasing? Where does \(f\) have local extrema?

Solution

14: \(f\) always increasing (no extrema); \(f\) has inflection at \(x = 0\)

15: \(f\) increasing for \(x < 0.5\), decreasing for \(x > 0.5\); local max at \(x = 0.5\)

16: \(f\) always increasing (no extrema); always concave up

17: \(f\) increasing on \((0, \pi/2) \cup (3\pi/2, 2\pi)\); local max at \(x = \pi/2\), local min at \(x = 3\pi/2\)

18: \(f\) always increasing (always positive derivative); inflection at \(x = 0\) (where \(f'\) has maximum)

19: \(f\) decreasing on \((-1, 1)\), increasing on \((-\infty, -1) \cup (1, \infty)\); local extrema at \(x = \pm 1\)

20: \(f\) increasing for \(x < 0\), increasing then decreasing for \(0 < x < 1\), decreasing for \(x > 1\); local max at \(x = 1\)

11 Problem 21: Comprehensive Analysis (xxx)

Given \(f(x) = x^4 - 4x^3 + 4x^2\):

Find \(f'(x)\) and \(f''(x)\).
Find all critical points and classify them.
Find all inflection points.
Determine intervals where \(f\) is increasing/decreasing and concave up/down.
Sketch the graphs of \(f(x)\), \(f'(x)\), and \(f''(x)\) on the same set of axes.

Solution

Derivatives: \[f'(x) = 4x^3 - 12x^2 + 8x = 4x(x^2 - 3x + 2) = 4x(x-1)(x-2)\] \[f''(x) = 12x^2 - 24x + 8 = 4(3x^2 - 6x + 2)\] Using quadratic formula: \(x = \frac{6 \pm \sqrt{36-24}}{6} = \frac{6 \pm \sqrt{12}}{6} = 1 \pm \frac{1}{\sqrt{3}}\)
Critical points: \(x = 0, 1, 2\)
- Test \(f''\) at critical points:
  - \(f''(0) = 8 > 0\) → local minimum
  - \(f''(1) = 12 - 24 + 8 = -4 < 0\) → local maximum
  - \(f''(2) = 48 - 48 + 8 = 8 > 0\) → local minimum
Inflection points: \(x = 1 \pm \frac{\sqrt{3}}{3} \approx 0.42, 1.58\)
Intervals:
- Increasing: \((0, 1)\) and \((2, \infty)\)
- Decreasing: \((-\infty, 0)\) and \((1, 2)\)
- Concave up: \((-\infty, 1-\frac{\sqrt{3}}{3}) \cup (1+\frac{\sqrt{3}}{3}, \infty)\)
- Concave down: \((1-\frac{\sqrt{3}}{3}, 1+\frac{\sqrt{3}}{3})\)
Graphs:

Three side-by-side graphs are shown. Left: f(x) = x^4 - 4x^3 + 4x^2 is a W-shaped quartic with local minima at x = 0 and x = 2 (both y = 0), a local maximum at x = 1 (y = 1), and inflection points marked with squares. Middle: f’(x) = 4x^3 - 12x^2 + 8x is a cubic with three zeros at x = 0, 1, 2, crossing the x-axis at each critical point. Right: f’’(x) = 12x^2 - 24x + 8 is a parabola with zeros at the inflection points (approximately x = 0.42 and x = 1.58).

12 Problem 22: Business Application (xxx)

A company’s revenue over 10 months is modeled by: \[R(t) = -t^3 + 9t^2 - 15t + 50\]

where \(t\) is months and \(R\) is in thousands €.

When is revenue increasing? Decreasing?
When does revenue reach local extrema? What is the revenue at these points?
When is the rate of revenue change accelerating? Decelerating?
Interpret all results in business terms.

Solution

Revenue rate: \[R'(t) = -3t^2 + 18t - 15 = -3(t^2 - 6t + 5) = -3(t-1)(t-5)\]
- Increasing: \(1 < t < 5\) (where \(R' > 0\))
- Decreasing: \(0 < t < 1\) and \(t > 5\) (where \(R' < 0\))
Local extrema:
- \(t = 1\): \(R(1) = -1 + 9 - 15 + 50 = 43\) thousand € (local minimum)
- \(t = 5\): \(R(5) = -125 + 225 - 75 + 50 = 75\) thousand € (local maximum)
Acceleration: \[R''(t) = -6t + 18 = -6(t - 3)\]
- Accelerating: \(t < 3\) (where \(R'' > 0\))
- Decelerating: \(t > 3\) (where \(R'' < 0\))
- Inflection: \(t = 3\), \(R(3) = -27 + 81 - 45 + 50 = 59\) thousand €
Business interpretation:

Two side-by-side graphs are shown. Left: Revenue R(t) is a cubic curve with key points marked at t = 1 (local minimum, 43k euros), t = 3 (inflection point, 59k euros), and t = 5 (local maximum, 75k euros), after which revenue declines. Right: The revenue growth rate R’(t) is a downward-opening parabola that crosses zero at t = 1 and t = 5, with a shaded positive region between them indicating the period of revenue growth. The maximum growth rate occurs at t = 3.

Narrative:

Month 1: Company hits revenue bottom (€43K) - turnaround point
Months 1-3: Revenue growing with increasing momentum (accelerating growth)
Month 3: Peak growth rate - fastest revenue increase
Months 3-5: Revenue still growing but momentum slowing (decelerating growth)
Month 5: Peak revenue (€75K) - market saturation reached
After Month 5: Revenue declining - time to pivot or innovate

Strategic recommendations:

Before Month 1: Implement cost-cutting measures
Months 1-3: Invest aggressively in growth (high ROI period)
Month 3: Optimal time for expansion or new product launch
Month 5: Prepare diversification strategy
After Month 5: Execute pivot or cost optimization

13 Problem 23: Challenge Problem (xxxx)

Consider the piecewise function:

\[f(x) = \begin{cases} x^2 & \text{if } x < 1 \\ 3 - x & \text{if } x \geq 1 \end{cases}\]

Is \(f\) continuous at \(x = 1\)?
Is \(f\) differentiable at \(x = 1\)?
Sketch \(f(x)\) and \(f'(x)\).
Classify \(x = 1\) (corner, cusp, or smooth?).

Solution

Continuity at \(x = 1\):
- \(\lim_{x \to 1^-} f(x) = 1^2 = 1\)
- \(\lim_{x \to 1^+} f(x) = 3 - 1 = 2\)
- \(f(1) = 3 - 1 = 2\) (using the definition for \(x \geq 1\))
- Since \(\lim_{x \to 1^-} f(x) = 1 \neq 2 = f(1)\), \(f\) is NOT continuous at \(x = 1\)
Differentiability at \(x = 1\):
- Since \(f\) is not continuous at \(x = 1\), it cannot be differentiable there
Graphs:

Two side-by-side graphs are shown. Left: f(x) is a piecewise function with x^2 for x < 1 and 3 - x for x >= 1. There is a jump discontinuity at x = 1, with an open circle at (1, 1) and a filled circle at (1, 2). A dashed vertical line marks the discontinuity. Right: f’(x) shows 2x for x < 1 (approaching 2 from below) and -1 for x > 1. Open circles at (1, 2) and (1, -1) indicate the derivative does not exist at x = 1, labeled DNE.

Classification:
- \(x = 1\) is a jump discontinuity, not a corner or cusp
- Corners and cusps require continuity
- This is more severe - the function jumps from one value to another