Session 05-04 - Chain Rule & Implicit Differentiation

Section 05: Differential Calculus

Entry Quiz - 10 Minutes

Quick Review from Session 05-03

Test your understanding of differentiation rules

1. Find the derivative of \(f(x) = (x^2 + 1)(3x - 2)\).

2. Differentiate \(g(x) = \frac{x^2}{x + 1}\) using the quotient rule.

3. For \(h(x) = 5x^{10} - 3x^2 + 7\), find \(h'(x)\).

4. What is the tangent line to \(f(x) = x^2\) at \(x = 3\)?

Homework Discussion - 15 Minutes

Your questions from Session 05-03

What questions do you have regarding the tasks?

Learning Objectives

What You’ll Learn Today

• Master the chain rule for differentiating composite functions
• Combine chain rule with product and quotient rules effectively
• Use implicit differentiation when you can’t solve for \(y\)
• Apply related rates to problems where quantities change over time
• Solve business problems with nested functions and changing rates

. . .

NoteKey Insight

The chain rule unlocks differentiation of composite functions, one of the most powerful and widely used techniques in calculus!

Part A: The Chain Rule

The Challenge: Composite Functions

The Problem: How do we differentiate \((x^2 + 3x + 1)^{100}\)?

• Could we expand it? No! Expansion would have hundreds of terms
• Current rules don’t help: Not a simple power, product, or quotient
• This is a composite function: A function inside another function

. . .

The Structure:

• Outer function: \(f(u) = u^{100}\)
• Inner function: \(u = x^2 + 3x + 1\)
• Composite: \(f(g(x)) = (x^2 + 3x + 1)^{100}\)

The Chain Rule

Derivative of outer (evaluated at inner) times derivative of inner:

. . .

\[\frac{d}{dx}[f(g(x))] = f'(g(x)) \cdot g'(x)\]

. . .

Or in Leibniz notation, if \(y = f(u)\) and \(u = g(x)\):

\[\frac{dy}{dx} = \frac{dy}{du} \cdot \frac{du}{dx}\]

. . .

Most Common Mistake: Forgetting to multiply by the derivative of the inner function!

Chain Rule Example

Example: Differentiate \(f(x) = (x^2 + 3x + 1)^{100}\)

. . .

Step 1: Identify inner and outer

• Outer: \(f(u) = u^{100}\), so \(f'(u) = 100u^{99}\)
• Inner: \(u = x^2 + 3x + 1\), so \(u' = 2x + 3\)

. . .

Step 2: Apply chain rule \[f'(x) = 100(x^2 + 3x + 1)^{99} \cdot (2x + 3)\]

. . .

Notice: We never had to expand the original function!

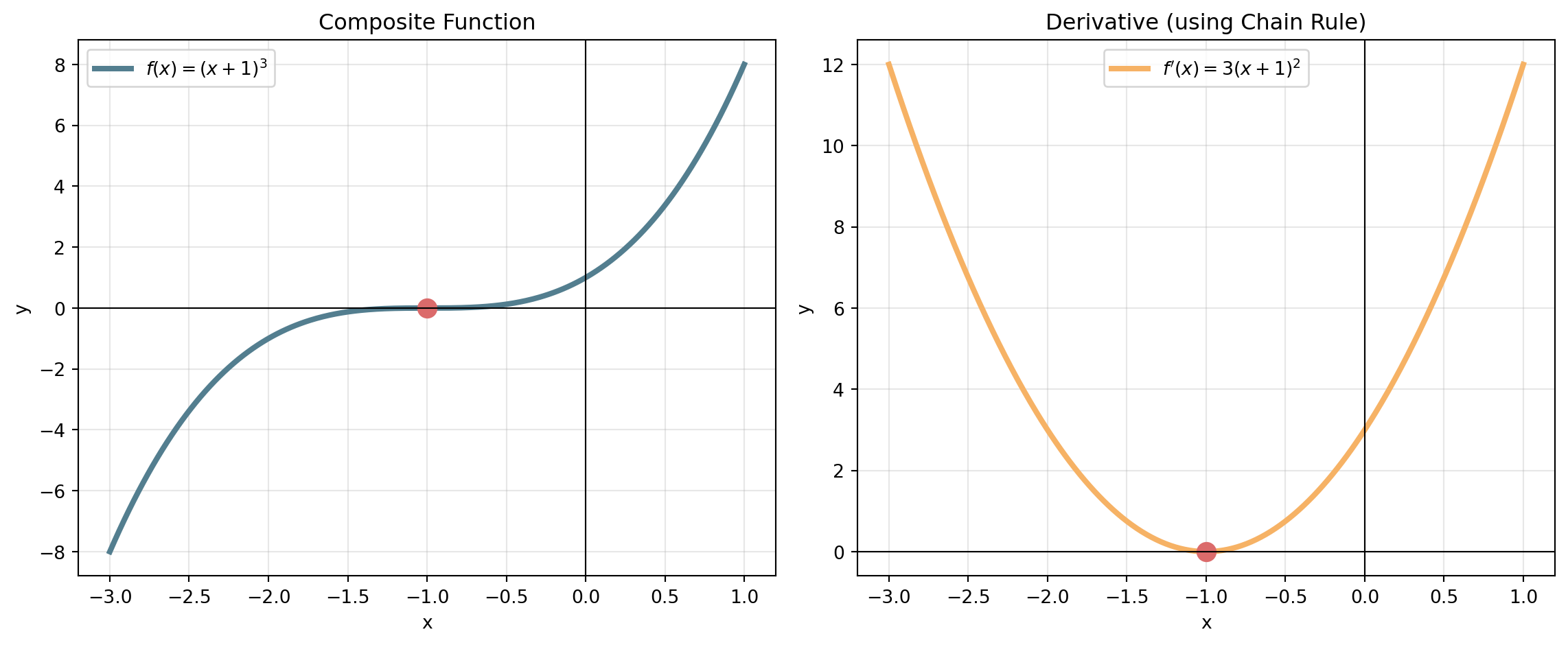
Visualizing the Chain Rule

. . .

• At \(x = -1\), both the function and derivative equal zero
• The derivative is always non-negative (parabola opening upward)

More Chain Rule Examples

Example: Differentiate \(g(x) = \sqrt{3x^2 + 5}\)

. . .

Rewrite: \(g(x) = (3x^2 + 5)^{1/2}\)

• Outer: \(u^{1/2}\), so derivative is \(\frac{1}{2}u^{-1/2}\)
• Inner: \(3x^2 + 5\), so derivative is \(6x\)
• \(g'(x) = \frac{1}{2}(3x^2 + 5)^{-1/2} \cdot 6x = \frac{6x}{2\sqrt{3x^2 + 5}} = \frac{3x}{\sqrt{3x^2 + 5}}\)

. . .

Example: Differentiate \(h(x) = \frac{1}{(2x - 1)^3}\)

. . .

Rewrite: \(h(x) = (2x - 1)^{-3}\)

. . .

• \(h'(x) = -3(2x - 1)^{-4} \cdot 2 = \frac{-6}{(2x - 1)^4}\)

Part B: Combining the Chain Rule

Chain Rule with Product Rule I

Strategy: When you have a product with composite functions:

1. Apply product rule first (outer operation)
2. Use chain rule for each composite factor

. . .

Example: Differentiate \(f(x) = x^2(3x + 1)^5\)

Chain Rule with Product Rule II

Product rule:

• \(u = x^2\), so \(u' = 2x\)
• \(v = (3x + 1)^5\), so \(v' = 5(3x + 1)^4 \cdot 3 = 15(3x + 1)^4\) (chain rule!)
• \(f'(x) = 2x(3x + 1)^5 + x^2 \cdot 15(3x + 1)^4\)

. . .

Factor:

• \(= (3x + 1)^4[2x(3x + 1) + 15x^2]\)
• \(= (3x + 1)^4[6x^2 + 2x + 15x^2]\)
• \(= (3x + 1)^4(21x^2 + 2x)\)

Simplified Chain Applications

Example: Differentiate \(h(x) = \sqrt{(2x + 1)^3}\)

. . .

Simplify first!

. . .

\[h(x) = (2x + 1)^{3/2}\]

. . .

\[h'(x) = \frac{3}{2}(2x + 1)^{1/2} \cdot 2\]

. . .

\[h'(x) = 3\sqrt{2x + 1}\]

Quick Practice - 10 Minutes

Individual Exercise

Work individually for 10 minutes

Differentiate using the chain rule:

1. \(f(x) = (5x + 2)^4\)

2. \(g(x) = \sqrt{x^2 - 1}\)

3. \(h(x) = (x^2 + 1)^3(2x - 1)^2\)

4. \(k(x) = \frac{x}{(3x + 1)^2}\)

Break - 10 Minutes

Part C: Implicit Differentiation

Two Ways to Find a Derivative

Problem: Revenue constraint \(pq = 10000\). Find \(\frac{dq}{dp}\).

. . .

Solve First

1. \(q = \frac{10000}{p} = 10000p^{-1}\) (Solve for \(q\) then differentiate)
2. \(\frac{dq}{dp} = -10000p^{-2} = -\frac{10000}{p^2}\)

Differentiate Directly

1. \(\frac{d}{dp}[pq] = \frac{d}{dp}[10000]\) (Differentiate both sides with respect to \(p\))
2. \(\frac{d}{dp}[p] \cdot q + p \cdot \frac{d}{dp}[q] = 0\) (Apply product rule on the left)
3. \(q + p\frac{dq}{dp} = 0\) (Solve for \(\frac{dq}{dp}\))
4. \(\frac{dq}{dp} = -\frac{q}{p}\) (Substitute the original constraint)
5. \(\frac{dq}{dp} = -\frac{10000/p}{p} = -\frac{10000}{p^2}\)

. . .

Both methods give \(\frac{dq}{dp} = -\frac{10000}{p^2}\). Method 2 is called implicit differentiation.

Why Learn Implicit Differentiation?

Because sometimes Method 1 is impossible or complex!

. . .

Factory produces constant output \(Q = 100\) with labor \(L\) and capital \(K\):

\[L^{0.6} \cdot K^{0.4} = 100\]

. . .

When we write \(L^{0.6} \cdot K^{0.4} = 100\), we’re really saying:

\[L^{0.6} \cdot [K(L)]^{0.4} = 100\]

. . .

Question: What does this mean?

. . .

Every variable is secretly a function!

The Main Idea

\(K\) depends on \(L\), we just don’t know the explicit formula!

\[L^{0.6} \cdot K^{0.4} = 100\]

. . .

The Chain Rule applies:

. . .

\[\frac{d}{dL}[K^{0.4}] = 0.4 \cdot K^{-0.6} \cdot \frac{dK}{dL}\]

. . .

NoteCore Principle

Whenever you differentiate a term containing \(K\), multiply by \(\frac{dK}{dL}\) because \(K\) is a function of \(L\).

Production Example

Step 1: Differentiate both sides with respect to \(L\)

\[\frac{d}{dL}[L^{0.6} \cdot K^{0.4}] = \frac{d}{dL}[100]\]

. . .

Step 2: Apply product rule on left side and solve for \(\frac{dK}{dL}\)

\[0.6L^{-0.4} \cdot K^{0.4} + L^{0.6} \cdot 0.4K^{-0.6} \cdot \frac{dK}{dL} = 0\]

. . .

\[\frac{dK}{dL} = -\frac{0.6L^{-0.4} \cdot K^{0.4}}{0.4L^{0.6} \cdot K^{-0.6}} = -\frac{0.6}{0.4} \cdot \frac{K}{L} = -\frac{3K}{2L}\]

Interpreting the Result

What does this mean?

\[\frac{dK}{dL} = -\frac{3K}{2L}\]

. . .

• The negative sign: more labor → less capital needed (trade-off)
• The ratio \(\frac{K}{L}\) matters: if \(K = 20\) and \(L = 10\), then \(\frac{dK}{dL} = -3\)
• Each additional unit of labor saves 3 units of capital
• Marginal Rate of Technical Substitution (MRTS) in economics!

. . .

The MRTS tells managers how to substitute between inputs while maintaining the same output level, crucial for cost minimization!

Example: Constant Revenue

A company sells a product with a constant revenue of 5000:

. . .

Practice: \(pq = 5000\). Find \(\frac{dq}{dp}\) using implicit differentiation.

. . .

Result: \(\frac{dq}{dp} = -\frac{q}{p}\)

. . .

Interpretation: At any point on the demand curve, a 1% price increase requires approximately a 1% quantity decrease to maintain revenue.

. . .

NoteWhen to Use Each Method

• Solve first if it’s easy (linear equations, simple fractions)
• Implicit differentiation when solving is messy or impossible
• You need the rate of change without fully solving the equation

Part D: Related Rates

Introduction to Related Rates

The Concept: When two or more quantities are related by an equation and both change with time, their rates of change are also related.

. . .

General Process:

1. Write an equation relating the quantities
2. Differentiate both sides with respect to time \(t\)
3. Substitute known values
4. Solve for the unknown rate

. . .

Related rates problems use implicit differentiation with respect to time!

Growing Customer Base

Scenario: A company’s revenue \(R\) depends on its customer base \(C\): \[R = 50\sqrt{C}\]

The company is gaining 100 new customers per month. How fast is revenue growing when \(C = 10000\) customers?

. . .

Step 1: Given relationship \(R = 50C^{1/2}\)

. . .

Step 2: Differentiate to time \(\frac{dR}{dt} = 50 \cdot \frac{1}{2}C^{-1/2} \cdot \frac{dC}{dt} = \frac{25}{\sqrt{C}} \cdot \frac{dC}{dt}\)

. . .

Step 3: Substitute given: \(\frac{dC}{dt} = 100\) customers/month, \(C = 10000\)

. . .

\[\frac{dR}{dt} = \frac{25}{\sqrt{10000}} \cdot 100 = \frac{25}{100} \cdot 100 = 25 \text{ €/month}\]

Business Related Rates Example

Scenario: A company’s profit \(P\) and market share \(m\) are related by: \[P = 1000m - 20m^2\]

where \(P\) is in k € and \(m\) is market share percentage. Market share is increasing at 2% per month. How fast is profit changing when \(m = 15\)%?

. . .

Step1: Differentiate \(\frac{dP}{dt} = 1000\frac{dm}{dt} - 40m\frac{dm}{dt} = (1000 - 40m)\frac{dm}{dt}\)

. . .

Step 2: Substitute given \(\frac{dm}{dt} = 2\) %/month, \(m = 15\) %

. . .

\[\frac{dP}{dt} = (1000 - 40 \cdot 15)(2) = (1000 - 600)(2) = 800\]

. . .

Answer: Profit is increasing at €800,000 per month.

Guided Practice

Practice Set A: Chain Rule Applications

Work in pairs for 15 minutes

Differentiate the following:

1. \(f(x) = (x^3 - 2x + 1)^{10}\)

2. \(g(x) = \sqrt{5x^2 + 3x - 1}\)

3. \(h(x) = \frac{1}{(x^2 + 1)^3}\)

4. \(k(x) = x(2x - 3)^4\)

Practice Set B: Implicit & Related

Continue working in pairs for 10 minutes

Implicit Differentiation:

1. A company’s marketing \(M\) and sales \(S\) satisfy \(MS = 5000\). Find \(\frac{dS}{dM}\).

2. Budget constraint: \(2L + 3K = 120\) where \(L\) = labor, \(K\) = capital. Find \(\frac{dK}{dL}\).

Related Rates:

3. Revenue \(R = 100Q - 0.5Q^2\) and quantity grows at 10 units/month. Find \(\frac{dR}{dt}\) when \(Q = 50\).

Coffee Break - 15 Minutes

Business Applications

Nested Economic Functions

Business Context: A company’s revenue depends on price \(p\), which itself depends on quantity \(x\):

• Price function: \(p(x) = 100 - 0.5x\)
• Revenue from price: \(R(p) = p(200 - 2p)\)

. . .

Question: Find \(\frac{dR}{dx}\), rate of change of revenue with respect to quantity.

. . .

Any idea how to approach this problem?

Chain Rule for Nested Functions I

. . .

Step 1: Express \(R\) in terms of \(p\) with \(R(p) = 200p - 2p^2\)

. . .

\[\frac{dR}{dp} = 200 - 4p\]

. . .

Step 2: Find \(\frac{dp}{dx}\) with \(p(x) = 100 - 0.5x\)

. . .

\[\frac{dp}{dx} = -0.5\]

. . .

Step 3: Apply chain rule \(\frac{dR}{dx} = \frac{dR}{dp} \cdot \frac{dp}{dx}\)

. . .

\[\frac{dR}{dx} = (200 - 4p)(-0.5)\]

Chain Rule for Nested Functions II

Now just substitute \(p = 100 - 0.5x\) into expression for \(\frac{dR}{dx}\):

. . .

\[\frac{dR}{dx} = (200 - 4(100 - 0.5x))(-0.5)\]

. . .

\[\frac{dR}{dx} = 100 - x\]

. . .

• At \(x\), revenue changes at \((100 - x)\) € per unit
• When \(x = 50\): \(\frac{dR}{dx} = 50\) (revenue still increasing)
• When \(x = 100\): \(\frac{dR}{dx} = 0\) (revenue maximized!)

Collaborative Problem-Solving

Challenge: Expanding Retail Chain

A retail chain’s profit \(P\) (in €1000) and stores \(n\) are related by:

\[P = 200\sqrt{n} - 5n\]

The company opens 4 new stores per year.

1. Write the relationship between \(\frac{dP}{dt}\) and \(\frac{dn}{dt}\).

2. How fast is profit changing when \(n = 25\) stores?

3. How fast is profit changing when \(n = 100\) stores?

4. At how many stores does profit stop growing? What does this mean for the company?

5. Discussion: Why does profit growth slow as the chain expands?

Think-Pair-Share

Discussion Question

Think individually, then discuss with class

Question: You’re analyzing two companies:

• Company A: Revenue \(R_A = (1000 + 50t)^{1.1}\) where \(t\) is years
• Company B: Revenue \(R_B = 1100 + 50t\)

At \(t = 0\), both have revenue of 1000 (thousand €).

1. Which company’s revenue is growing faster at \(t = 0\)?
2. Will this always be the case?
3. What does the exponent 1.1 tell you about A’s growth strategy?

Wrap-Up & Key Takeaways

Today’s Essential Techniques

Technique	When to Use	Key Idea
Chain Rule	Composite \(f(g(x))\)	Outer derivative × inner derivative
Chain + Product	Product with composites	Product rule first, then chain
Implicit Diff	Variables intertwined	Differentiate both, solve for derivative
Related Rates	Quantities change over time	Differentiate with respect to \(t\)

. . .

Never forget the inner derivative! This is the main mistake in chain rule problems.

Final Assessment - 5 Minutes

Quick Check

Work individually and then we compare

1. Differentiate \((3x^2 + 1)^4\).

2. Price \(p\) and quantity \(q\) satisfy \(pq = 800\). Find \(\frac{dq}{dp}\).

3. Profit \(P = 50\sqrt{Q}\) and production grows at 8 units/month. How fast is profit growing when \(Q = 100\)?

4. True or False: \(\frac{d}{dx}[f(g(x))] = f'(x) \cdot g'(x)\)

Next Session Preview

Session 05-05

Graphical Calculus Mastery

• From \(f\) to \(f'\): Sketching derivatives from function graphs
• From \(f'\) to \(f\): Determining function properties from derivative
• Second derivatives: Understanding \(f''\) and concavity
• Critical points: Where \(f'(x) = 0\) or doesn’t exist
• Inflection points: Where \(f''(x) = 0\) and concavity changes
• Heavily tested on exams! Visual analysis is crucial

. . .

Complete Tasks 05-04!