Session 04-04 - Introduction to Trigonometric Functions

Section 04: Advanced Functions

Author

Dr. Nikolai Heinrichs & Dr. Tobias Vlćek

Entry Quiz

Review from Session 04-03

Work individually for 5 minutes, then we discuss

  1. Evaluate: \(e^{\ln(5)}\)

  2. If an investment grows from 1000 EUR to 2000 EUR in 8 years with continuous compounding, what is the annual rate \(r\)? (Use \(A = Pe^{rt}\))

  3. Solve: \(2^{3x-1} = 64\)

  4. A bacteria population doubles every 4 hours. If you start with 100 bacteria, write the exponential model \(N(t)\) where \(t\) is in hours.

Homework Discussion

Your questions from Tasks 04-03

Focus on exponential functions and applications

  • Challenges with exponential growth and decay models
  • Compound interest calculations (discrete vs. continuous)
  • Half-life and doubling time problems
  • Comparing exponential vs. polynomial growth rates
  • Real-world modeling (bookings, savings, learning curves)

Trigonometry introduces periodic (repeating) behavior - a new type of function compared to the always-increasing exponentials! Instead of continuous growth, we’ll see cycles and oscillations.

Learning Objectives

Today’s Goals

By the end of this session, you will be able to:

  • Understand angles in degrees and radians
  • Define sine, cosine, and tangent using the unit circle
  • Calculate exact values for special angles
  • Sketch basic trigonometric function graphs
  • Identify amplitude, period, and phase shifts
  • Apply trigonometry to real-world periodic phenomena

Measuring Angles

Degrees vs. Radians

Two ways to measure angles

  • Full rotation = 360°
  • Right angle = 90°
  • Straight angle = 180°
  • Historical: Based on ancient calendars
  • Full rotation = \(2\pi\) radians
  • Right angle = \(\frac{\pi}{2}\) radians
  • Straight angle = \(\pi\) radians
  • Radians make calculus formulas simpler!
  • They’re the “natural” unit for mathematics

Conversion: \(180° = \pi \text{ radians}\), \(1° = \frac{\pi}{180}\) radians and \(1 \text{ radian} = \frac{180°}{\pi}\)

Why Radians Are Natural

The arc length connection

For a circle with radius \(r\) and central angle \(\theta\) (in radians):

\[\text{Arc length } s = r\theta\]

Why is this great?

  • If \(\theta = 1\) radian, then arc length = radius (that’s the definition!)
  • For a full circle: \(s = r \cdot 2\pi = 2\pi r\) (the circumference formula!)
  • No conversion factors needed - it just works!

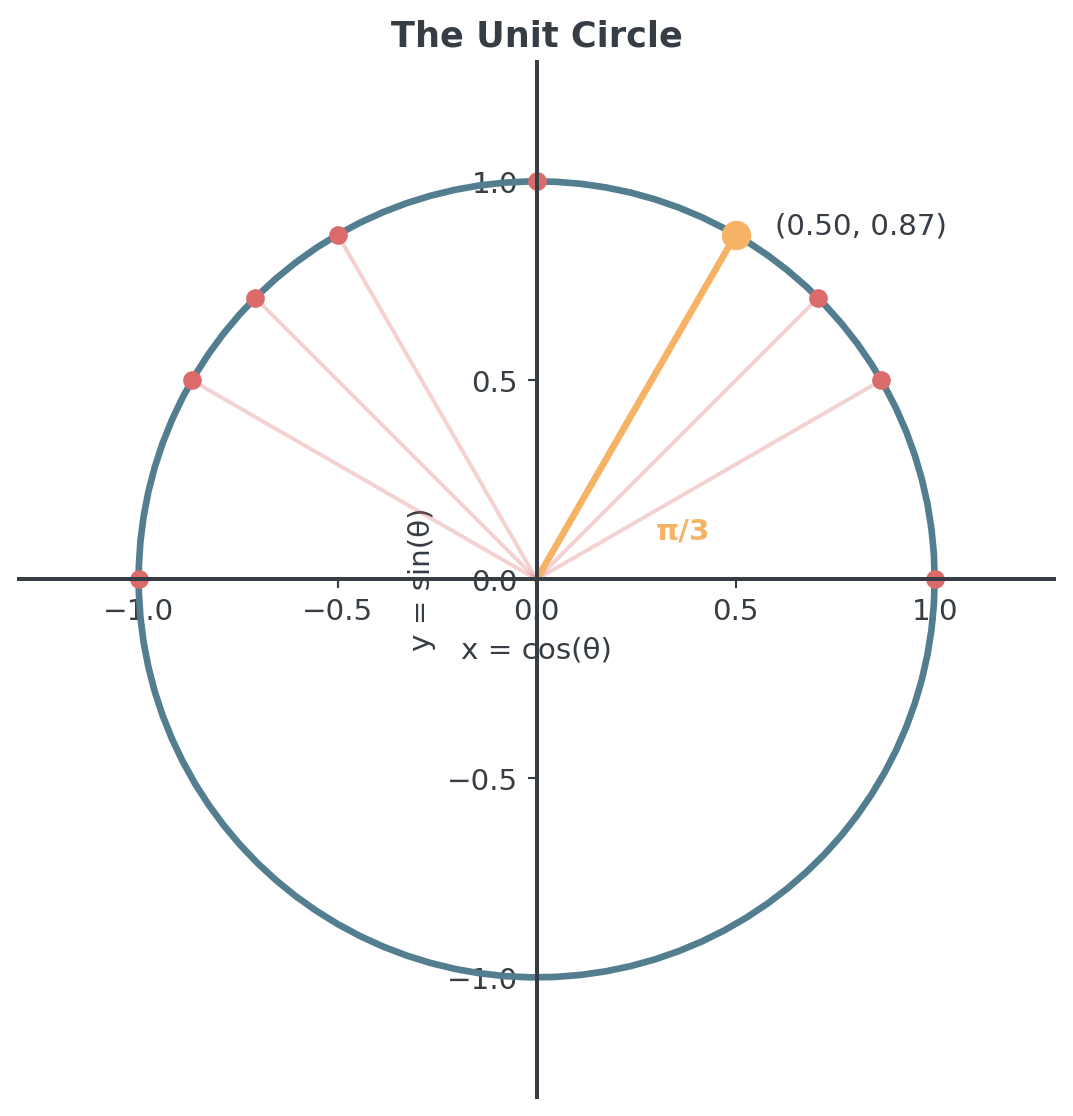
The Unit Circle

Defining the Unit Circle I

The unit circle is a circle with:

  • Center at the origin (0, 0)
  • Radius = 1
  • Equation: \(x^2 + y^2 = 1\)

For any angle \(\theta\) from the positive x-axis:

  • The point on the circle is \((\cos\theta, \sin\theta)\)
  • This is the fundamental definition!

Every point on the unit circle can be written as \((cos θ, sin θ)\) for some angle θ!

Defining the Unit Circle II

Unit circle around the origin with radius lines to the special angles 0, π/6, π/4, π/3, π/2, 2π/3, 3π/4, 5π/6 and π. The angle π/3 is highlighted and its point on the circle labelled (0.50, 0.87): the x-coordinate is the cosine of the angle, the y-coordinate its sine.

Think-Pair-Share: Unit Circle

2 minutes individual, 3 minutes pairs, 2 minutes class discussion

Find the coordinates on the unit circle

For each angle, find the point (cos θ, sin θ):

  1. θ = π/2
  2. θ = π
  3. θ = 3π/2
  4. θ = 2π

Discuss: What pattern do you notice as we go around the circle?

Sine and Cosine

Sine Function Graph

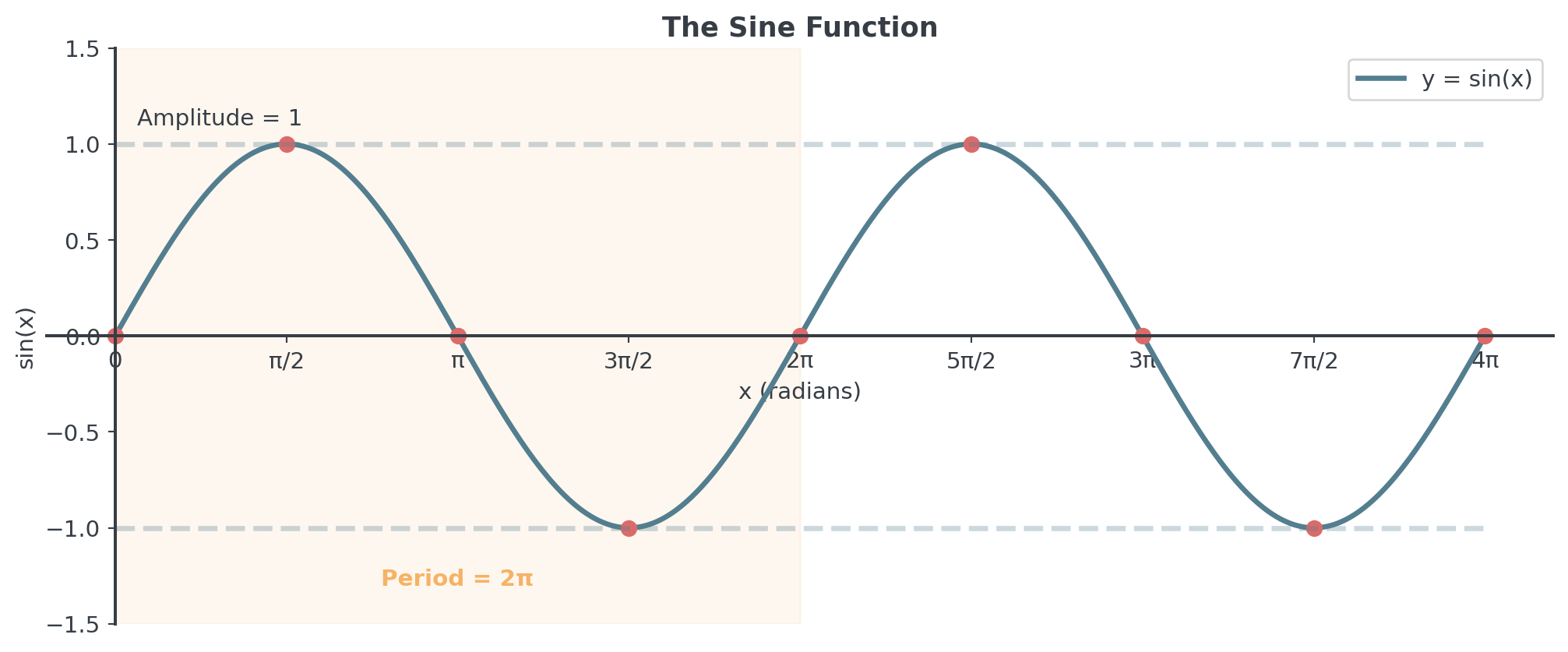
Sine curve from 0 to 4π: two full waves between the dashed lines at 1 and -1 (amplitude 1). It starts at 0, peaks at π/2, crosses zero at π, reaches its minimum at 3π/2 and returns to 0 at 2π. The first period of 2π is shaded; then the pattern repeats.

Domain: All real numbers, range: [-1; 1], period: 2π

Cosine Function Graph

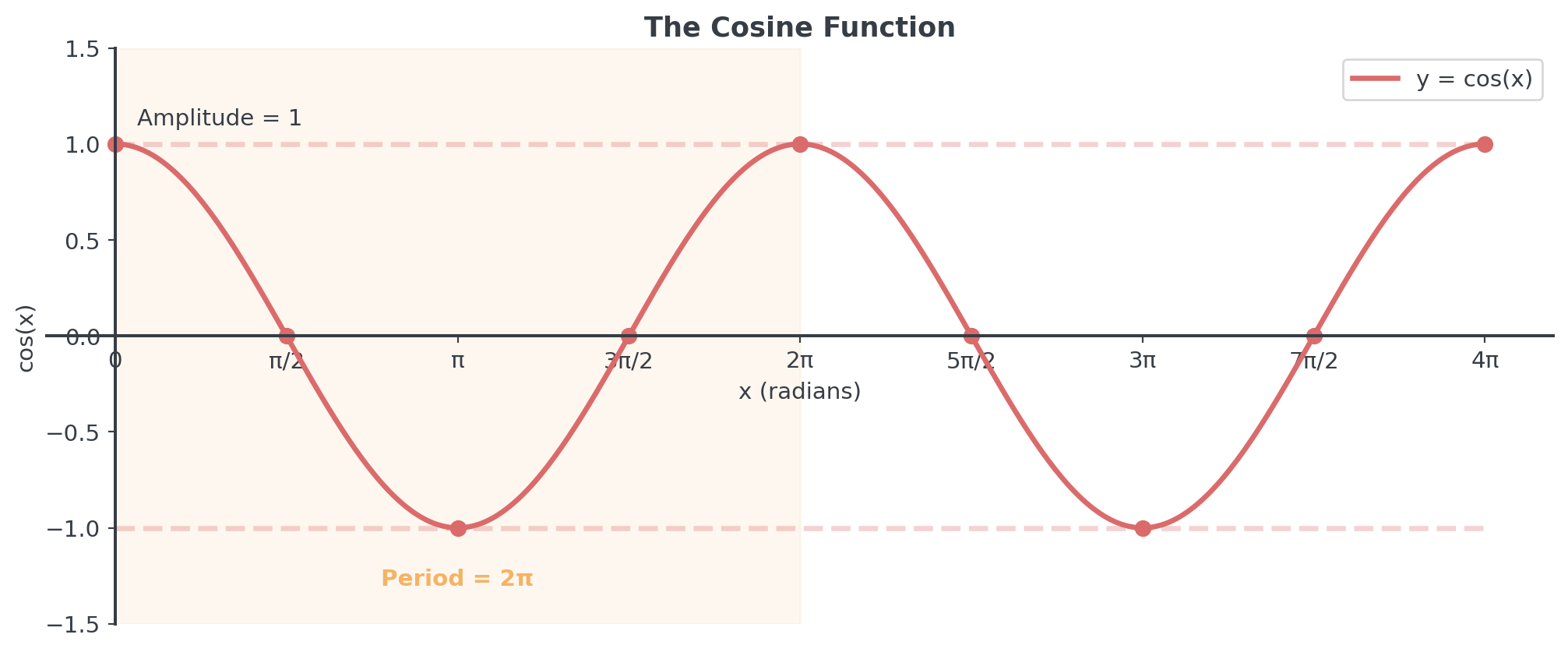
Cosine curve from 0 to 4π: two full waves between the dashed lines at 1 and -1. It starts at its maximum 1, crosses zero at π/2, reaches -1 at π and is back at 1 at 2π. The first period of 2π is shaded. The shape is that of the sine curve, shifted by π/2.

Domain: All real numbers, range: [-1; 1], period: 2π -> Shifted by π/2

Negative Transformations

Understanding -sin(x) and -cos(x)

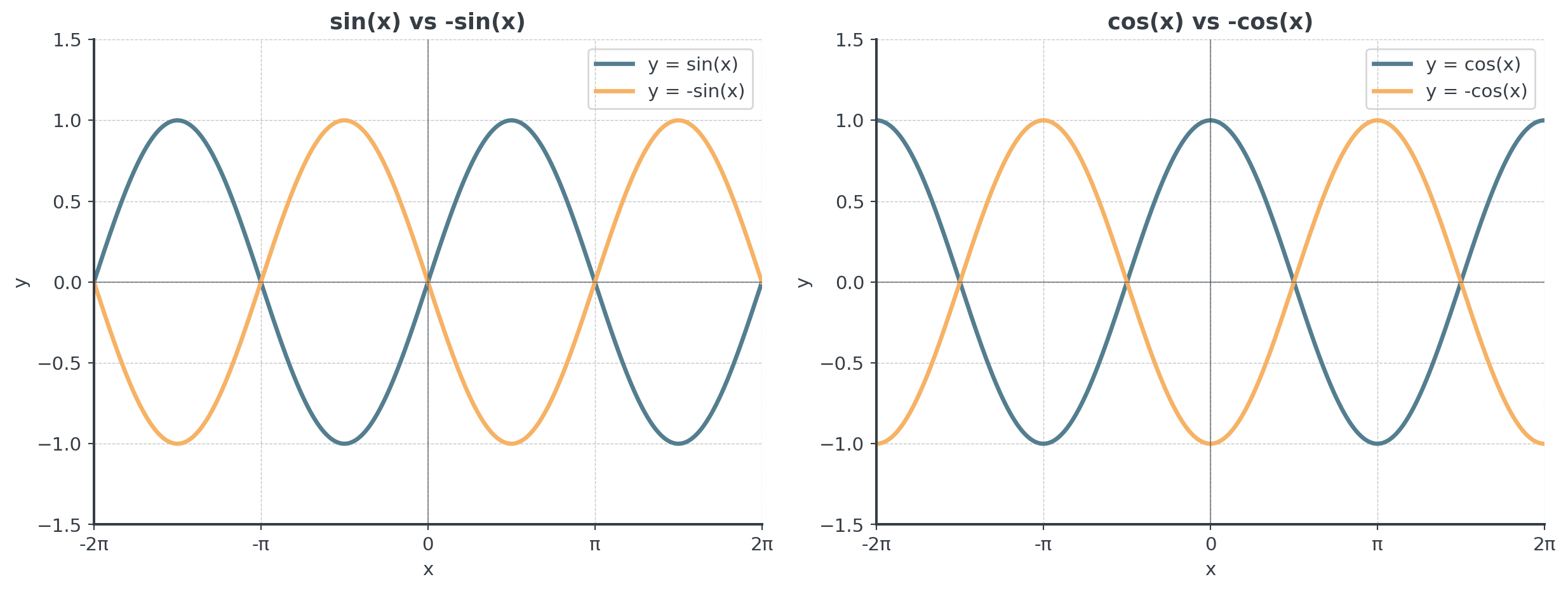
Two panels from -2π to 2π. Left: sin(x) and -sin(x). Right: cos(x) and -cos(x). In each panel the negated curve is the mirror image of the original across the x-axis: where one has a peak the other has a trough, and both cross zero at the same places.

Multiplying by -1 creates a reflection across the x-axis!

The Tangent Function

Definition and Graph

The ratio that creates asymptotes

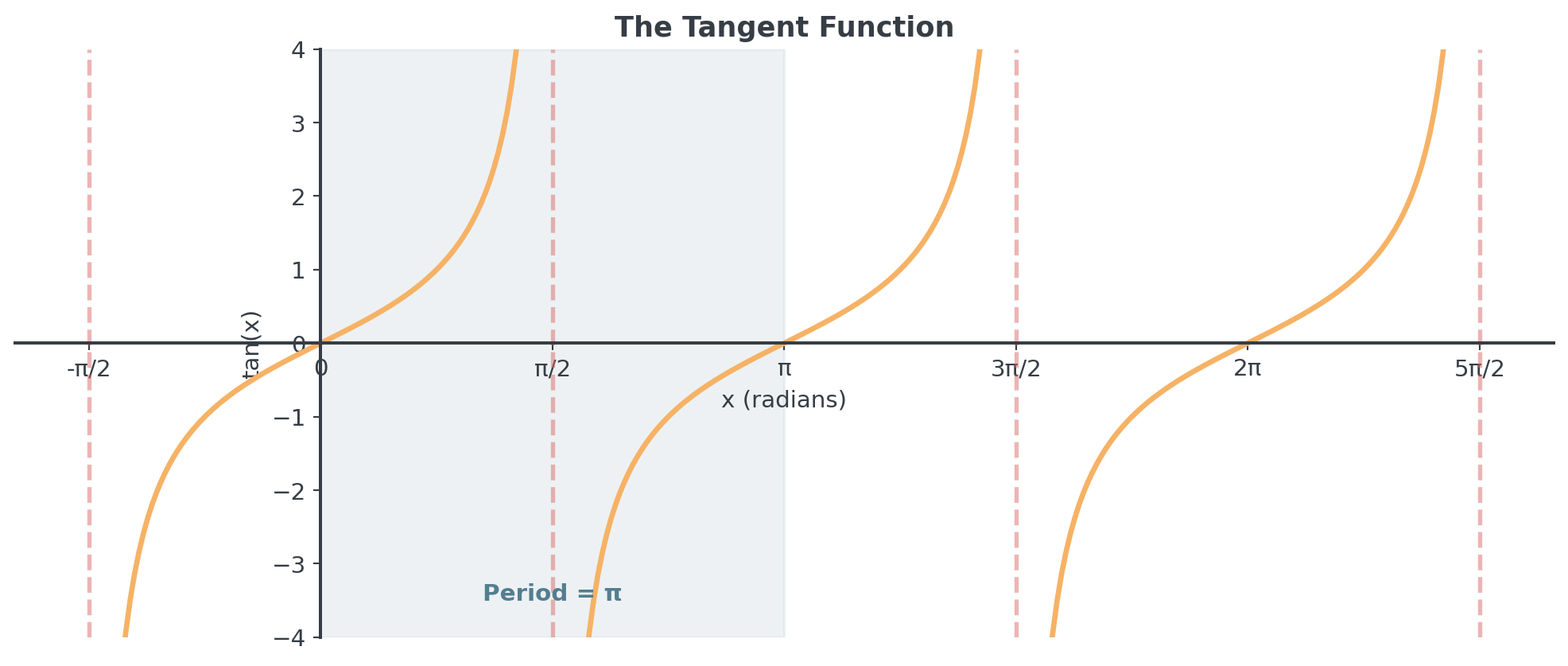
Tangent curve from -π/2 to 5π/2 in three separate branches. Each branch rises from far below to far above the x-axis between dashed vertical asymptotes at -π/2, π/2, 3π/2 and 5π/2, crossing zero at 0, π and 2π. The pattern repeats with period π.

Why Tangent Matters

Understanding slopes and angles

The tangent function has a special geometric meaning:

\[\tan(\theta) = \frac{\sin(\theta)}{\cos(\theta)}\]

Why Tangent Matters II

  • Navigation & Surveying: Finding heights of buildings or mountains
  • Physics: Calculating angles of projectile motion or inclined planes
  • Computer Graphics: Rotating objects and calculating viewing angles

However, it is likely not important for the FSP and thus we won’t go into too much detail here!

Calculator: Trigonometry

Make sure angle mode is set correctly!

Check indicator: D = Degrees, R = Radians

Function Keys
\(\sin(x)\) sin
\(\cos(x)\) cos
\(\tan(x)\) tan
\(\sin^{-1}(x)\) SHIFT + sin
\(\tan^{-1}(x)\) SHIFT + tan

Example: \(\sin(30°) = 0.5\)

Amplitude and Period

Transformations of Sine & Cosine I

Modifying the basic wave

General form: \(y = A\sin(B(x - C)) + D\)

  • A: Amplitude (height of wave)
  • B: Affects period (Period = 2π/B)
  • C: Phase shift (horizontal shift)
  • D: Midline \(y = D\) (vertical shift)
TipYou already know the order from functions!

Apply transformations in this order: horizontal stretch/compress, horizontal shift, vertical stretch/compress, vertical shift.

Transformations of Sine & Cosine II

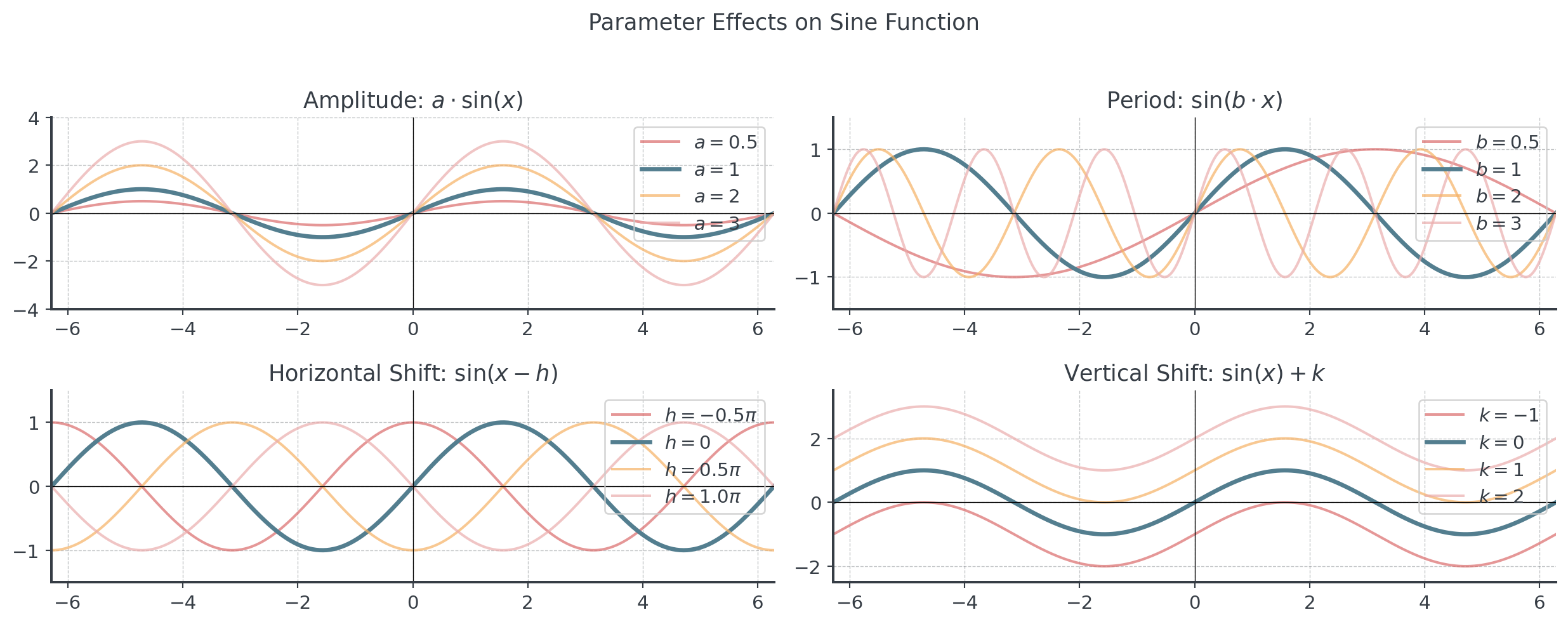
Four panels on how each parameter changes the sine wave. Amplitude, a sin(x) for a = 0.5, 1, 2, 3: a larger a gives taller waves. Period, sin(bx) for b = 0.5, 1, 2, 3: a larger b packs more waves into the same width. Horizontal shift, sin(x - h): the same wave moved sideways. Vertical shift, sin(x) + k for k = -1, 0, 1, 2: the same wave moved up or down.

Spot the Error: Trigonometry

Can you identify the errors? Work with your neighbor

Time allocation: 5 minutes to find errors, 5 minutes to discuss

Student work:

  1. “Since sin(30°) = 0.5, then sin(60°) = 1”

  2. “tan(90°) = sin(90°)/cos(90°) = 1/0 = ∞”

  3. “The period of sin(3x) is 6π”

  4. “cos²(x) + sin²(x) = 1 only when x = 0”

Reflect

Quickly think about these questions

  • How are sine and cosine related to the unit circle?
  • Why do we use radians instead of degrees in calculus?
  • Think of real-world examples of periodic behavior
  • Can you name three phenomena that oscillate?

Break

Applications

Sound Waves I

Music is trigonometry

A pure musical tone: \(y = A\sin(2\pi ft)\)

  • A = amplitude (volume)
  • f = frequency (pitch)
  • t = time

Question: What happens if we increase the frequency?

Example: Middle A (440 Hz) \[y = \sin(2\pi \cdot 440 \cdot t) = \sin(880\pi t)\]

Sound Waves II

Two sine waves over 0.01 seconds, one above the other. The 440 Hz tone (middle A) completes about four and a half cycles, the 880 Hz tone one octave higher about nine. One period is shaded in each panel; at 880 Hz it is half as wide, because doubling the frequency halves the period.

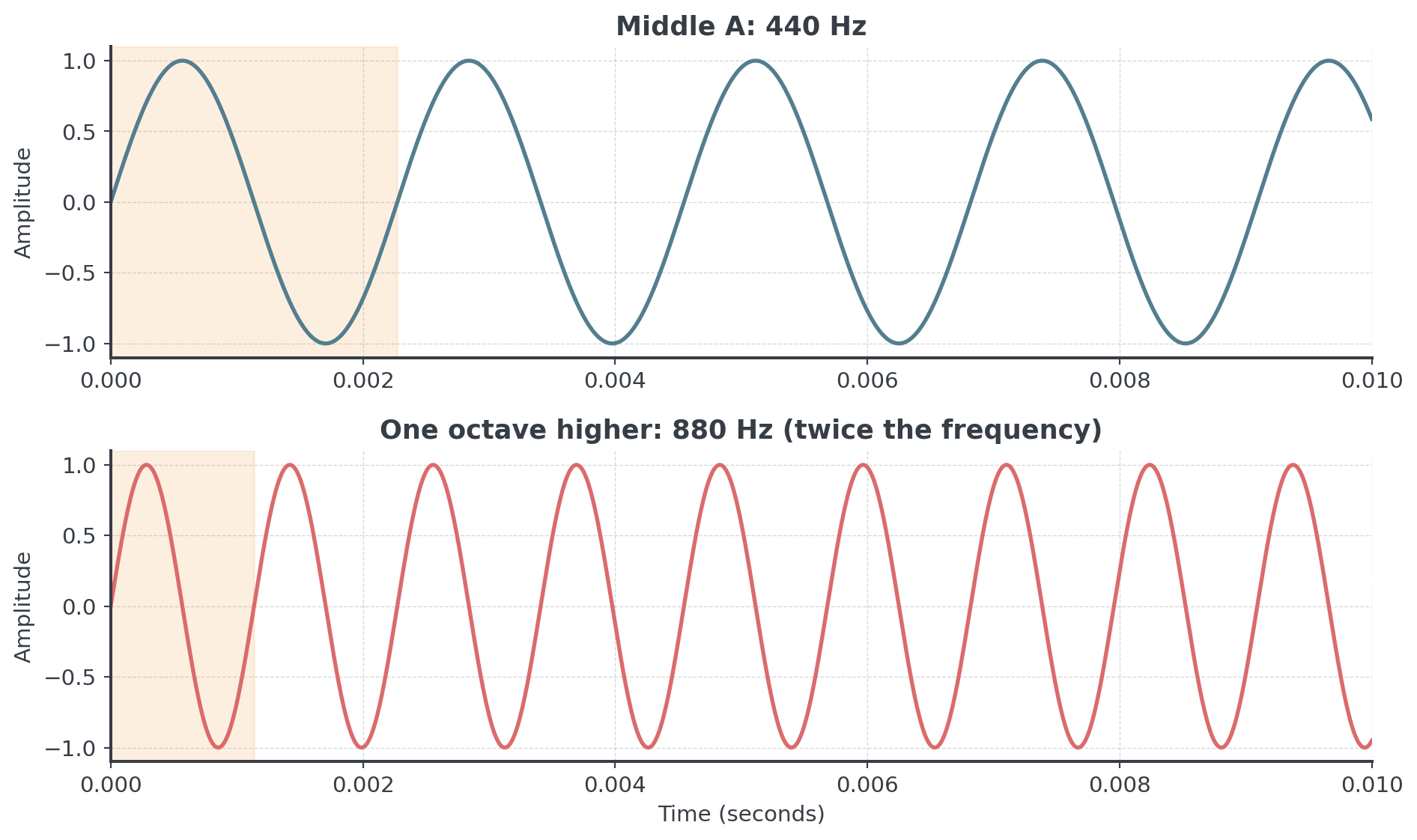
Notice: Doubling the frequency halves the period! The 880 Hz wave completes two cycles in the same time as 440 Hz completes one.

Seasonal Patterns I

Temperature variation

Average daily temperature in many locations: \[T(d) = A\sin\left(\frac{2\pi}{365}(d - C)\right) + T_{avg}\]

  • d = day of year
  • A = amplitude (half the difference between summer/winter)
  • \(T_{avg}\) = average yearly temperature
  • C = phase shift (adjusts when the peak occurs - typically 80-110 days)

Seasonal Patterns II

Hamburg’s temperature model

Using real Hamburg climate data (Weather Spark):

  • Average annual temperature: \(T_{avg} = 9.2°C\)
  • Warmest month (July): ~18°C
  • Coldest months (Jan/Feb): ~1°C
  • Amplitude: \(A = 8.5°C\)

\[T(d) = 8.5\sin\left(\frac{2\pi}{365}(d - 105)\right) + 9.2\]

Seasonal Patterns III

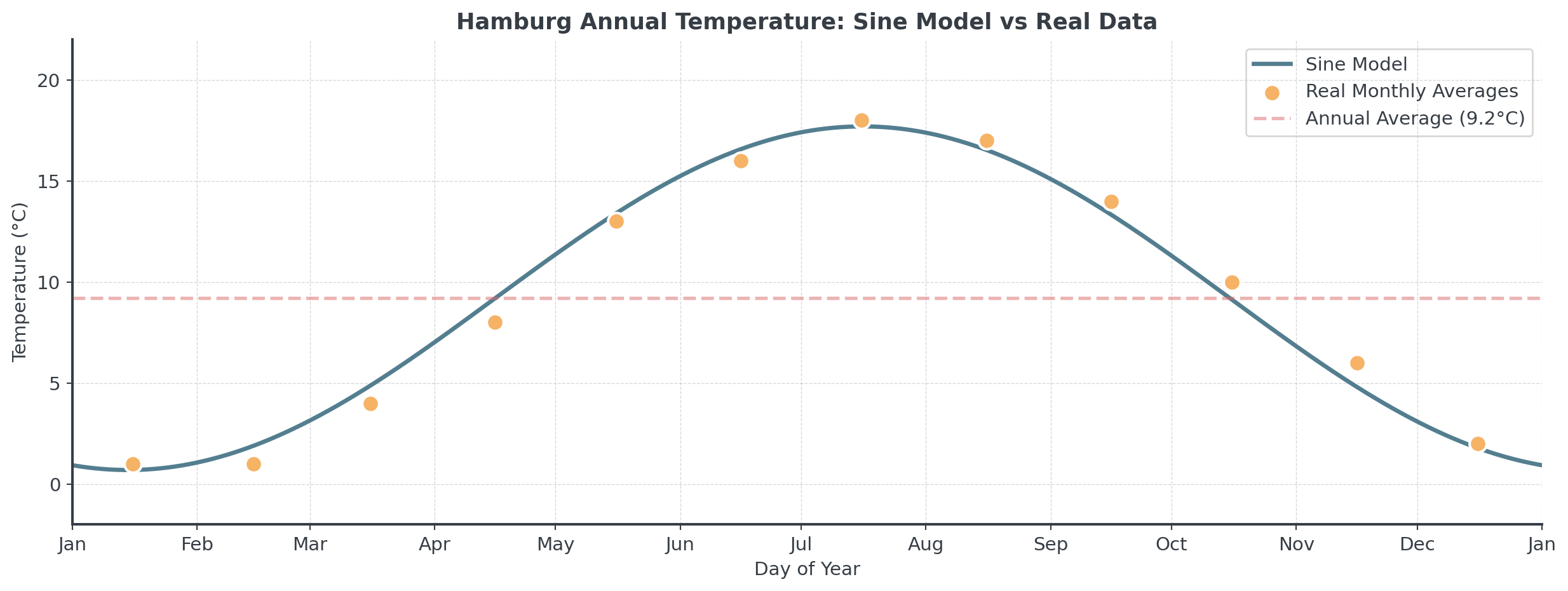
Sine model of Hamburg's temperature over the year, with twelve monthly averages as dots. The curve swings around the dashed annual average of 9.2°C, from about 0.7°C in mid-January to about 17.7°C in mid-July. The dots, from 1°C in January and February up to 18°C in July, lie close to the curve.

The sine function provides an great fit to Hamburg’s real climate data!

Guided Practice

Task 1: Function Properties

Work alone for 5 minutes, then discuss for 3 minutes

For \(y = 3\sin(2x) - 1\), find:

  1. Amplitude
  2. Period
  3. Midline
  4. Range

Task 2: Tidal Heights

Work alone for 5 minutes, then discuss for 3 minutes

The water depth in a harbor varies with the tides. At high tide, the water is 12 meters deep. At low tide, it is 4 meters deep. High tide occurs at noon, and the tide cycle repeats every 12 hours.

Write a function d(t) for the water depth t hours after noon.

Hint: What is the average depth? What is the amplitude?

Task 3: Matching Graphs

Work in pairs for 5 minutes, then discuss for 3 minutes

Match each equation to its description:

Equations:

  1. \(y = 2\sin(x)\)

  2. \(y = \sin(2x)\)

  3. \(y = \sin(x) + 2\)

  4. \(y = \sin\left(x + \frac{\pi}{2}\right)\)

Descriptions:

  1. Is shifted up 2 units
  2. Has amplitude 2
  3. Completes two cycles in 2π
  4. Looks like the cosine function

Task 4: Blood Pressure Modeling

Work alone for 7 minutes, then discuss for 4 minutes

A person’s blood pressure oscillates with each heartbeat. Suppose a person has: a maximum pressure (systolic): 120 mmHg, minimum pressure (diastolic): 80 mmHg and a heart rate: 72 beats per minute.

Questions:

  1. What is the amplitude of the blood pressure oscillation?
  2. What is the period in minutes?
  3. Write a function P(t) for blood pressure at time t minutes, assuming pressure starts at maximum.

Task 5: Ferris Wheel Challenge

Work alone for 5 minutes, then discuss for 3 minutes
A Ferris wheel with radius 20 meters completes one rotation every 4 minutes. The bottom of the wheel is 2 meters above ground. Write a function for the height of a rider at time t (in minutes), starting at the bottom.
Hints to consider:

  • What is the center height of the wheel?
  • What is the amplitude of the up-and-down motion?
  • What is the period of rotation?
  • Which function starts at the bottom: sine or cosine?

Inverse Trigonometry

Brief Addition

Going backwards

Sometimes we need to find the angle:

  • If sin(θ) = 0.5, what is θ?
  • Answer: θ = arcsin(0.5) = π/6 (or 30°)

Question: But wait! Doesn’t sin(150°) also equal 0.5?

Yes! That’s why we need restrictions…

Restricted Inverse

The inverse functions

  • arcsin(x) or sin⁻¹(x): gives angle whose sine is x
  • arccos(x) or cos⁻¹(x): gives angle whose cosine is x
  • arctan(x) or tan⁻¹(x): gives angle whose tangent is x

To make inverses work, we restrict the output ranges (also called principal values):

  • arcsin: [-π/2; π/2] (from -90° to 90°)
  • arccos: [0; π] (from 0° to 180°)
  • arctan: (-π/2; π/2) (from -90° to 90°, not including endpoints)

Visualizing Inverse Relationships

How sine and its inverse relate

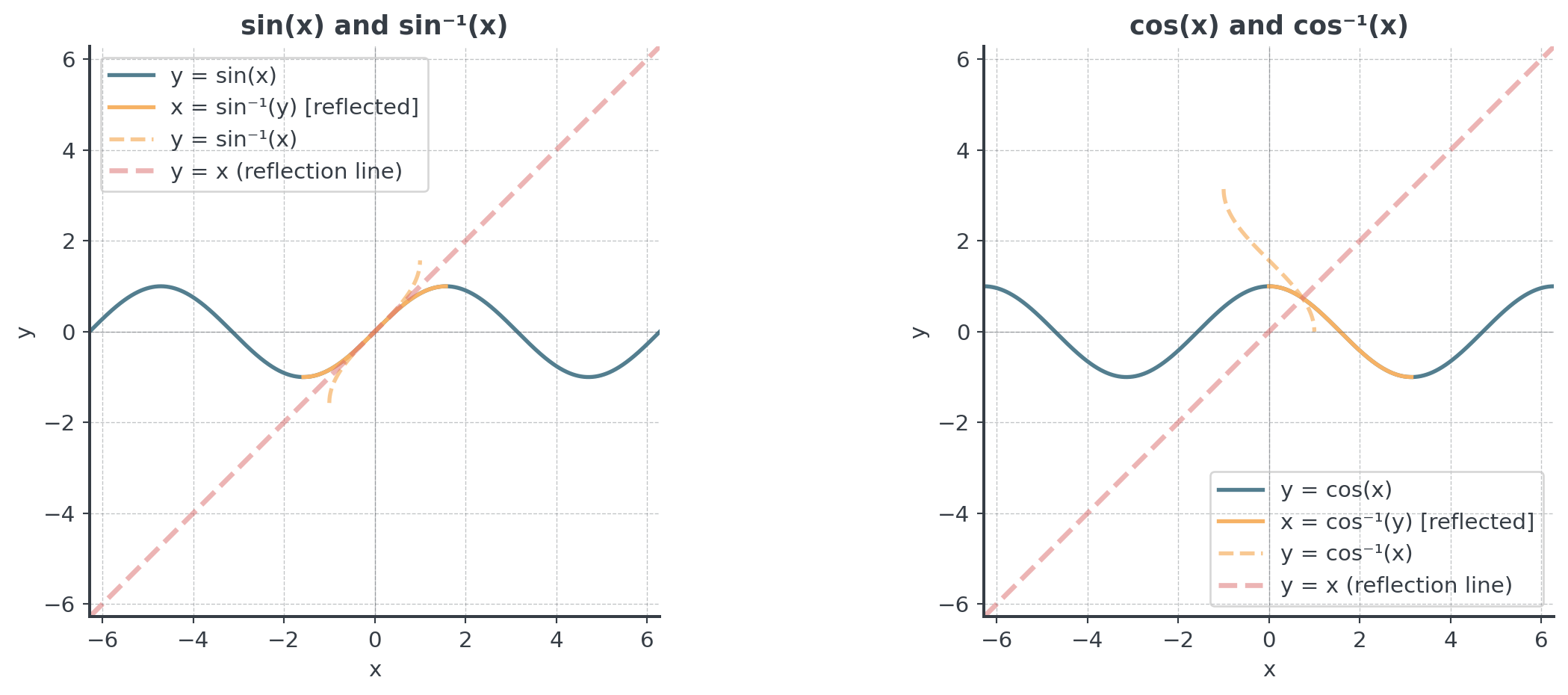
Two panels with the dashed diagonal y = x. Left: the sine wave, with its piece between -π/2 and π/2 highlighted, and the arcsine curve as the mirror image of that piece across the diagonal. Right: the cosine wave, with its piece between 0 and π highlighted, and the arccosine curve as its mirror image. Only the restricted piece is inverted.

Inverse functions are reflections across the line y = x.

Challenge Problem

Combining Waves

Work individually for 8 minutes, then discuss for 4 minutes

Consider two sound waves where the combined wave is: \(y = y_1 + y_2\).

  • Wave 1: \(y_1 = 2\sin(3x)\)
  • Wave 2: \(y_2 = \sin(3x + \pi)\)
  1. Use the fact that \(\sin(x + \pi) = -\sin(x)\) to simplify y in terms of a single sine function.
  2. What is the amplitude and period of the combined wave?

Combining Waves II

  1. What happens if Wave 2 had amplitude 2: \(y_2 = 2\sin(3x + \pi) = -2\sin(3x)\)?

Coffee Break

FSP Workshop

Problem 1: Lettuce Under LEDs

A vertical farm grows lettuce indoors under LED lights. It buys electricity on a dynamic tariff, so the price changes over the day. On a winter weekday, the price \(p(t)\) in cents per kWh follows a sinusoidal function of the time \(t\) in hours after midnight, for one day \(t \in [0; 24]\). The price is highest at 18:00 with 42 cents per kWh, its midline is 30 cents per kWh, and the pattern repeats every 24 hours.

  1. Give \(p(t)\) in the form \(A\cos(B(t - C)) + D\) and explain how you find each parameter. Determine the lowest price and the time when it occurs. [4 pts.]

LEDs: The Dark Block

The lettuce needs 8 hours of darkness per day in one block. The farm switches the LEDs off during the 8 hours with the highest prices and runs them for the other 16 hours.

  1. Explain why this block lies symmetrically around 18:00 and determine it. Compute the price at its start and at its end. [4 pts.]

(for verification: \(p(t) = 12\cos\left(\frac{\pi}{12}(t - 18)\right) + 30\))

LEDs: Costs per Hour

While they are on, the LEDs draw 250 kW. So far, the farm ran them from 6:00 to 22:00.

  1. Give the lighting costs \(L(t)\) in EUR per hour while the LEDs are on and describe how the graph of \(L\) arises from the graph of \(p\). Determine the highest and the lowest hourly lighting cost with the new schedule from b) and compare the highest one with the old schedule. [4 pts.]

LEDs: The Summer Tariff

In summer, solar power flattens the curve. The price is highest at 20:00 with 38 cents per kWh and lowest with 22 cents per kWh. The period stays 24 hours.

  1. Show that the summer price is \(s(t) = \frac{2}{3}\,p(t - 2) + 10\). Describe the transformations from \(p\) to \(s\) in the correct order. Determine the summer dark block and the price at its ends. [4 pts.]

Key Concepts

Key Takeaways

You’ve learned

  • Angle measurement in degrees and radians
  • The unit circle and its significance
  • Sine, cosine, and tangent functions
  • Graphing and transformations
  • Real-world periodic phenomena

Final Assessment

5 minutes - Individual work

Quick Check:

  1. Convert 45° to radians

  2. What is the period of y = sin(4x)?

  3. What is the amplitude of y = -3cos(x) + 2?

Looking Ahead

Next Session: Mock Exam 05

Session 04-05 is exam only - no lecture

  • 90 minutes working time plus 5 minutes reading time, 50 points
  • Covers all of Section 04: polynomial, power, rational, exponential, logarithmic and trigonometric functions
  • Allowed: non-programmable calculator, drawing instruments, monolingual dictionary
  • Not allowed: notes, formula sheets, any electronic devices
  • Counts toward the 60% of test points needed for exam admission

Preparing for Mock Exam 05

Complete Tasks 04-04, then prepare for Mock Exam 05 with FSP Training 04 (sidebar, Section 04 worksheets). The mock exam builds on both!