Session 07-07 - Binomial & Geometric Distributions

Section 07: Probability & Statistics

Author

Dr. Nikolai Heinrichs & Dr. Tobias Vlćek

Entry Quiz - 10 Minutes

Quick Review from Session 07-06

From a contingency table, how do you calculate \(P(A|B)\)?
In a table with 200 total, 80 in category A, 60 in category B, and 30 in both. Find \(P(A|B)\).
How do you test if two variables are independent using a table?
A company has 1000 employees: 600 full-time, 400 with degrees, 280 full-time with degrees. Build the table.

Homework Discussion - 12 Minutes

Your Questions from Session 07-06

Let’s clarify contingency-table logic before distributions.

Marginal vs joint vs conditional probabilities
Denominator selection in conditional probabilities
Independence checks in tables

Learning Objectives

What You’ll Master Today

Identify binomial experiments and their requirements
Apply the binomial formula: \(P(X=k) = \binom{n}{k} p^k (1-p)^{n-k}\)
Calculate probabilities: “exactly k”, “at most k”, “at least k”
Use the hypergeometric distribution for sampling without replacement
Use the geometric distribution for “first success” problems
Use z-scores to compute normal probabilities

. . .

Binomial distribution problems appear on every Feststellungsprüfung!

Part A: Binomial Experiments

Discussion Prompt

Question: Discuss with a partner: What is the key decision rule from this part, and where can students confuse it on the exam?

Requirements for Binomial

Binomial Experiment Conditions

Fixed number of trials: \(n\) is known in advance
Two outcomes: Success (probability \(p\)) or Failure (probability \(1-p\))
Independence: Trials don’t affect each other
Constant probability: \(p\) is the same for all trials

. . .

Examples: - Flipping a coin 10 times (heads = success) - Testing 50 products (defective = success) - Surveying 100 customers (satisfied = success)

The Binomial Formula

Binomial Distribution

\[P(X = k) = \binom{n}{k} p^k (1-p)^{n-k}\]

Where: - \(n\) = number of trials - \(k\) = number of successes - \(p\) = probability of success - \(\binom{n}{k} = \frac{n!}{k!(n-k)!}\) = number of ways

Understanding the Formula

\[P(X = k) = \underbrace{\binom{n}{k}}_{\text{arrangements}} \times \underbrace{p^k}_{\text{k successes}} \times \underbrace{(1-p)^{n-k}}_{\text{n-k failures}}\]

. . .

Example: In 5 coin flips, \(P(\text{exactly 3 heads})\)?

\[P(X=3) = \binom{5}{3} \times (0.5)^3 \times (0.5)^2 = 10 \times 0.125 \times 0.25 = 0.3125\]

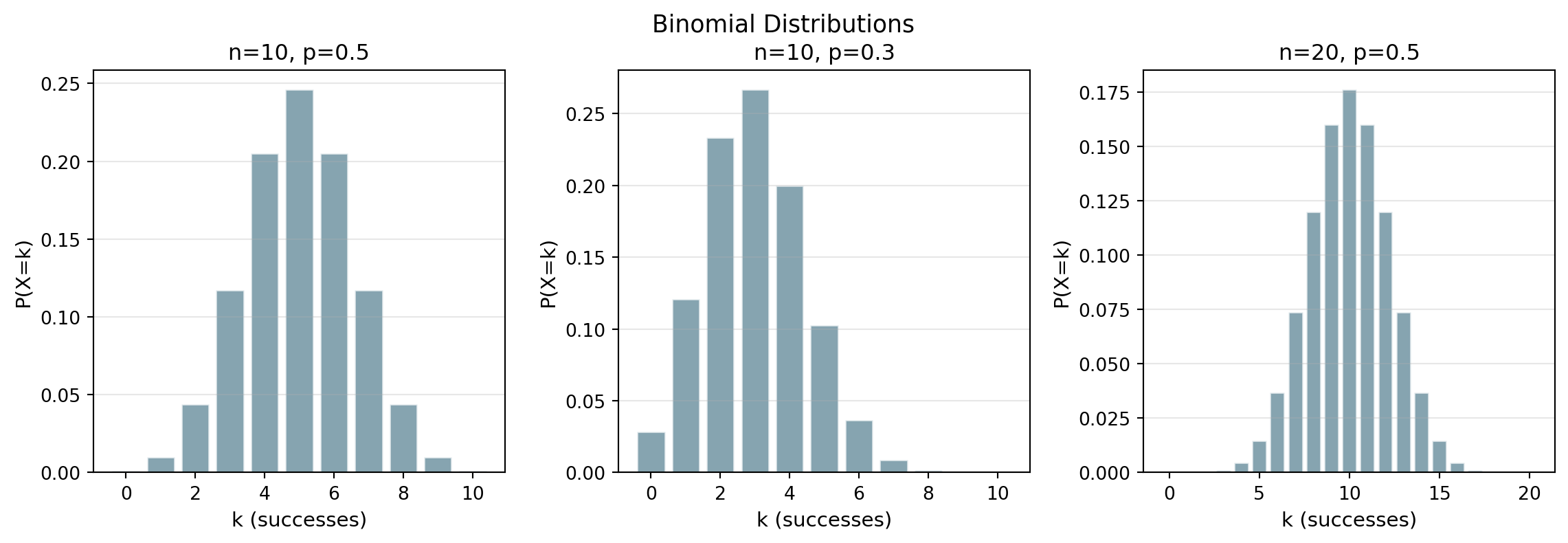
Binomial Distribution Visualization

Part B: Common Probability Questions

Discussion Prompt

Question: Discuss with a partner: What is the key decision rule from this part, and where can students confuse it on the exam?

Three Types of Questions

Question Type	Formula
Exactly k	\(P(X = k)\)
At most k	\(P(X \leq k) = \sum_{i=0}^{k} P(X=i)\)
At least k	\(P(X \geq k) = 1 - P(X < k) = 1 - P(X \leq k-1)\)

. . .

For “at least” problems, use the complement rule!

Wording Decoder (Exam Language)

Phrase	Mathematical form
exactly \(k\)	\(P(X=k)\)
at most \(k\)	\(P(X \le k)\)
at least \(k\)	\(P(X \ge k)=1-P(X\le k-1)\)
between \(a\) and \(b\) (inclusive)	\(P(a \le X \le b)\)
first success on trial \(n\)	geometric: \((1-p)^{n-1}p\)

Always check whether endpoints are included in words like “between”, “at most”, and “at least”.

Quick Check - 6 Minutes

Binomial or Geometric?

Work individually

Choose binomial or geometric for each:

Probability of exactly 4 defective items in 20 tested items.
Probability the first payment default occurs on the 7th customer.
Probability of at least 2 purchases out of 12 website visitors.

Example: Quality Control

A machine produces items with 8% defect rate. In a batch of 15 items:

\(P(\text{exactly 2 defective})\)

. . .

\[P(X=2) = \binom{15}{2} (0.08)^2 (0.92)^{13} = 105 \times 0.0064 \times 0.326 \approx 0.219\]

. . .

\(P(\text{at most 1 defective})\)

. . .

\[P(X \leq 1) = P(X=0) + P(X=1)\] \[= \binom{15}{0}(0.08)^0(0.92)^{15} + \binom{15}{1}(0.08)^1(0.92)^{14}\] \[= 0.286 + 0.373 = 0.659\]

Example Continued

\(P(\text{at least 2 defective})\)

. . .

\[P(X \geq 2) = 1 - P(X \leq 1) = 1 - 0.659 = 0.341\]

. . .

\(P(\text{between 1 and 3 defective, inclusive})\)

. . .

\[P(1 \leq X \leq 3) = P(X=1) + P(X=2) + P(X=3)\] \[\approx 0.373 + 0.219 + 0.085 = 0.677\]

Expected Value and Variance

Binomial Mean and Variance

Expected value (mean): \(\mu = E[X] = np\)
Variance: \(\sigma^2 = np(1-p)\)
Standard deviation: \(\sigma = \sqrt{np(1-p)}\)

. . .

Example: If \(n=100\) and \(p=0.3\): - Expected successes: \(\mu = 100 \times 0.3 = 30\) - Standard deviation: \(\sigma = \sqrt{100 \times 0.3 \times 0.7} = \sqrt{21} \approx 4.58\)

Part C: Hypergeometric Distribution

Discussion Prompt

Question: What changes in probability models when we sample without replacement?

When to Use Hypergeometric

The binomial assumes independent trials (with replacement). But what if we draw without replacement from a finite population?

Hypergeometric Setup

Use the hypergeometric distribution when:

Population size is fixed: \(N\)
There are \(K\) “success” items in the population
We draw \(n\) items without replacement
We ask for exactly \(k\) successes in the sample

Hypergeometric Formula

Probability of Exactly \(k\) Successes

\[P(X=k)=\frac{\binom{K}{k}\binom{N-K}{n-k}}{\binom{N}{n}}\]

Where:

\(N\) = population size
\(K\) = number of successes in population
\(n\) = sample size
\(k\) = successes in sample

Binomial vs Hypergeometric

Model	Typical wording	Replacement	Independence
Binomial	“in 20 trials”	with replacement / approx constant \(p\)	yes
Hypergeometric	“from a lot of 200 items”	without replacement	no

. . .

If sampling is without replacement from a finite population, do not use binomial automatically. Check whether hypergeometric is the correct model.

Worked Example 1: Quality Control

A lot has \(N=50\) items, with \(K=8\) defective. Sample \(n=5\) items without replacement.

Question: What is \(P(X=2)\), the probability of exactly 2 defectives?

\[P(X=2)=\frac{\binom{8}{2}\binom{42}{3}}{\binom{50}{5}}\]

\[=\frac{28\cdot11{,}480}{2{,}118{,}760}\approx0.152\]

Worked Example 2: Team Selection

From 18 applicants, 7 are international. Choose 5 without replacement.

Question: What is the probability of exactly 2 international students?

\[P(X=2)=\frac{\binom{7}{2}\binom{11}{3}}{\binom{18}{5}}\]

. . .

\[=\frac{3{,}465}{8{,}568}\approx0.404\]

. . .

If the population is very large compared with the sample, hypergeometric probabilities are often close to binomial with \(p=K/N\).

Break - 10 Minutes

Part D: Geometric Distribution

Discussion Prompt

Question: Discuss with a partner: What is the key decision rule from this part, and where can students confuse it on the exam?

Waiting for First Success

Geometric Distribution

The probability that the first success occurs on trial \(n\):

\[P(X = n) = (1-p)^{n-1} \cdot p\]

Where \(p\) = probability of success on each trial.

. . .

Example: A salesperson has a 20% chance of making a sale on each call. What’s the probability the first sale is on the 4th call?

\[P(X=4) = (0.8)^3 \times 0.2 = 0.512 \times 0.2 = 0.1024\]

Geometric: Expected Trials

Expected Number of Trials

For the geometric distribution: \[E[X] = \frac{1}{p}\]

. . .

Example: If success probability is 0.25, on average how many trials until first success?

\[E[X] = \frac{1}{0.25} = 4 \text{ trials}\]

Geometric Example: Exam Style

A machine produces defective items with probability 0.05.

\(P(\text{first defective item is the 10th produced})\)

\[P(X=10) = (0.95)^9 \times 0.05 = 0.631 \times 0.05 = 0.0316\]

. . .

\(P(\text{first defective item within first 5 items})\)

\[P(X \leq 5) = 1 - P(\text{no defective in first 5}) = 1 - (0.95)^5\] \[= 1 - 0.774 = 0.226\]

Solving for Minimum n (Exam Skill)

Question: How many items must be checked so that the probability of finding at least one defective item is at least 95%?

Given \(p=0.05\) defective probability per item:

\[1-(1-p)^n \geq 0.95\]

\[1-(0.95)^n \geq 0.95 \Rightarrow (0.95)^n \leq 0.05\]

Take logarithms:

\[n\ln(0.95) \leq \ln(0.05)\]

Because \(\ln(0.95)<0\), inequality direction flips when dividing:

\[n \geq \frac{\ln(0.05)}{\ln(0.95)} \approx 58.4\]

So the minimum whole number is:

\[n=59\]

Rounding Rule and Connection

Always round up for minimum required sample size.

. . .

Connection: Geometric and Binomial Complement

This same setup can be seen as:

\[P(\text{at least one defective in } n \text{ trials}) = 1 - P(X=0)\]

with \(X \sim \text{Binomial}(n,p)\), so

\[1 - (1-p)^n\]

This matches the geometric waiting-time interpretation.

Quick Practice

Solve for Minimum n

A call center has conversion probability \(p=0.12\) per call.

Find the minimum number of calls needed so that the probability of at least one conversion is at least 90%.

Part E: Geometric Cumulative and Memoryless Property

Discussion Prompt

Question: Which phrase signals a waiting-time model, and which phrase signals a fixed-trials model?

Geometric Cumulative Forms

For \(X \sim \text{Geometric}(p)\):

\[P(X=n)=(1-p)^{n-1}p\]
\[P(X\le n)=1-(1-p)^n\]
\[P(X>n)=(1-p)^n\]

. . .

These are very useful for “within first \(n\) trials” and “no success yet” questions.

Memoryless Property

Memoryless

For geometric \(X\):

\[P(X>m+n\mid X>m)=P(X>n)\]

If no success has happened yet, the process restarts probabilistically.

Memoryless Example

A support agent closes tickets with probability \(p=0.25\) per call.

Question: Given no closure in first 4 calls, what is probability of no closure in the next 3 calls?

By memoryless property:

\[P(X>7\mid X>4)=P(X>3)=(0.75)^3\approx0.422\]

Common Wording Pitfall

“First success on trial 5” -> \(P(X=5)=(1-p)^4p\)
“At least one success in 5 trials” -> \(1-(1-p)^5\)

These are different events.

Part F: Normal Distribution with z-Scores

Discussion Prompt

Question: Why do we standardize to \(Z\) instead of using many different normal tables?

Standardization

If \(X \sim N(\mu,\sigma)\), then

\[Z=\frac{X-\mu}{\sigma} \sim N(0,1)\]

Use this to convert any normal probability into a standard normal probability.

Typical Probability Conversions

Question	Convert to Z-form
\(P(X\le a)\)	\(P\left(Z\le\frac{a-\mu}{\sigma}\right)\)
\(P(X\ge a)\)	\(1-P\left(Z\le\frac{a-\mu}{\sigma}\right)\)
\(P(a\le X\le b)\)	\(P\left(\frac{a-\mu}{\sigma}\le Z\le\frac{b-\mu}{\sigma}\right)\)

Worked Example 1: Left-Tail Probability

Delivery times are normal with mean 30 min and standard deviation 4 min.

Question: Find \(P(X\le 34)\).

\[z=\frac{34-30}{4}=1\]

\[P(X\le34)=P(Z\le1)\approx0.8413\]

Worked Example 2: Interval Probability

Using the same distribution, find \(P(28\le X\le36)\).

\[z_1=\frac{28-30}{4}=-0.5,\quad z_2=\frac{36-30}{4}=1.5\]

\[P(28\le X\le36)=P(-0.5\le Z\le1.5)\]

\[\approx 0.9332-0.3085=0.6247\]

Reverse Question (Quantile)

Exam scores are normal with \(\mu=70\), \(\sigma=10\).

Question: What score marks the top 10%?

Need \(P(X\le x)=0.90\), so \(z_{0.90}\approx1.2816\).

\[x=\mu+z\sigma=70+1.2816\cdot10\approx82.8\]

So the cutoff is about 83 points.

Quick Check - 6 Minutes

Normal Distribution Practice

Work individually

If \(X\sim N(100,15)\):

Compute the z-score for \(x=130\).
Write (do not evaluate) a formula for \(P(X\ge115)\) using \(Z\).
Is \(P(X\le85)\) greater than or less than 0.5?

Guided Practice - 20 Minutes

Practice Problem 1

A multiple choice test has 20 questions with 4 options each. A student guesses randomly on all questions.

What’s the probability of getting exactly 5 correct?
What’s the probability of getting at least 8 correct?
What’s the expected number of correct answers?
What’s the standard deviation?

Practice Problem 2 (Exam Style)

A company’s call center receives calls with 15% conversion rate.

In 10 calls, what’s the probability of exactly 2 conversions?
In 10 calls, what’s the probability of at least 1 conversion?
What’s the probability that the first conversion is on the 5th call?
On average, how many calls until the first conversion?

Chained Exam Mini-Problem - 8 Minutes

Work individually, then compare

A process has success probability \(p=0.10\) per trial.

Compute \(P(\text{at least one success in 8 trials})\).
Use the same setup to solve minimum \(n\) such that \(P(\text{at least one success})\ge0.95\).
Explain why part (b) must be rounded up.

Coffee Break - 10 Minutes

Collaborative Problem-Solving - 20 Minutes

Group Challenge: Sales Conversion Modeling

Think individually (2 min), pair (3 min), then work in groups of 3-4 and share

A sales rep has conversion probability \(p=0.18\) per call.

In 12 calls, compute probability of exactly 3 conversions.
In 12 calls, compute probability of at least 1 conversion.
Find the minimum number of calls needed for at least one conversion with probability at least 97%.
Explain in one sentence why question 3 requires rounding up.

Confidence Check - 2 Minutes

Rate your confidence for today’s goals on a 1-5 scale (1 = not confident, 5 = exam-ready):

Mapping wording to binomial/geometric formulas
Using complement strategies for “at least” questions
Solving minimum-\(n\) targets with logarithms and rounding

Final Assessment - 5 Minutes

Exit Ticket

Work individually

For \(X\sim \text{Binomial}(n=12,p=0.3)\), what is the formula for \(P(X=4)\)?
Write one expression for \(P(X\ge 1)\) in terms of \(n\) and \(p\).
If a minimum required sample size gives \(n \ge 14.2\), what integer must you choose?

Wrap-Up & Key Takeaways

Today’s Essential Concepts

Binomial formula: \(P(X=k) = \binom{n}{k}p^k(1-p)^{n-k}\)
Binomial parameters: \(\mu = np\), \(\sigma = \sqrt{np(1-p)}\)
Three question types: Exactly k, at most k, at least k
Hypergeometric: Without replacement from finite populations
Geometric: \((1-p)^{n-1} \cdot p\) for first success on trial \(n\)
Geometric cumulative + memoryless: efficient for waiting-time questions
z-score method: convert normal problems to standard normal

Next Session Preview

Coming Up: Mock Exam 2

Full 180-minute exam simulation
All Section 07 topics covered
Practice under exam conditions
Prepare your formula sheet!

. . .

Homework

Complete Tasks 07-07 - focus on binomial calculation practice!