Session 07-02 - Basic Probability Concepts

Section 07: Probability & Statistics

Author

Dr. Nikolai Heinrichs & Dr. Tobias Vlćek

Entry Quiz - 10 Minutes

Quick Review from Session 07-01

Test your understanding of Descriptive Statistics

Find the mean and median of: \(8, 12, 15, 9, 16, 12, 11\)
If the variance of a dataset is 16, what is the standard deviation?
A frequency table shows 15 out of 50 items are defective. What is the relative frequency of defective items?
What is the interquartile range if \(Q1 = 25\) and \(Q3 = 45\)?

Homework Discussion - 12 Minutes

Your Questions from Session 07-01

Focus on interpretation, not only computation.

Choosing mean vs median in skewed data
Reading histograms and box plots correctly
Interpreting relative frequencies in context

Learning Objectives

What You’ll Master Today

Define sample spaces and events using proper notation
Apply probability axioms: \(0 \leq P(A) \leq 1\)
Use the complement rule: \(P(A') = 1 - P(A)\)
Apply the addition rule: \(P(A \cup B) = P(A) + P(B) - P(A \cap B)\)
Distinguish between independent and mutually exclusive events
Define a random variable and read a simple PMF/CDF
Solve probability problems in business contexts

. . .

These concepts are fundamental for all probability calculations on the exam!

Part A: Sample Spaces and Events

Random Experiments

A random experiment is a process with uncertain outcomes.

. . .

Examples:

Rolling a die
Selecting a product for quality control
Surveying a customer about satisfaction
Measuring daily sales

. . .

Question: Do you know any other examples?

Sample Space

Definition: Sample Space (Ergebnismenge)

The sample space \(S\) (or \(\Omega\)) is the set of all possible outcomes of a random experiment.

. . .

Examples:

Experiment	Sample Space
Coin flip	\(S = \{H, T\}\)
Die roll	\(S = \{1, 2, 3, 4, 5, 6\}\)
Two coin flips	\(S = \{HH, HT, TH, TT\}\)

. . .

So far ok, right?

Events

Definition: Event (Ereignis)

An event \(A\) is a subset of the sample space \(S\).

. . .

Example: Die roll with \(S = \{1, 2, 3, 4, 5, 6\}\)

Event A: “Rolling an even number” = \(\{2, 4, 6\}\)
Event B: “Rolling greater than 4” = \(\{5, 6\}\)
Event C: “Rolling a 7” = \(\emptyset\) (impossible event)
Event D: “Rolling a positive number” = \(S\) (certain event)

. . .

Remember, \(\emptyset\) just means “nothing” while \(S\) means “everything”.

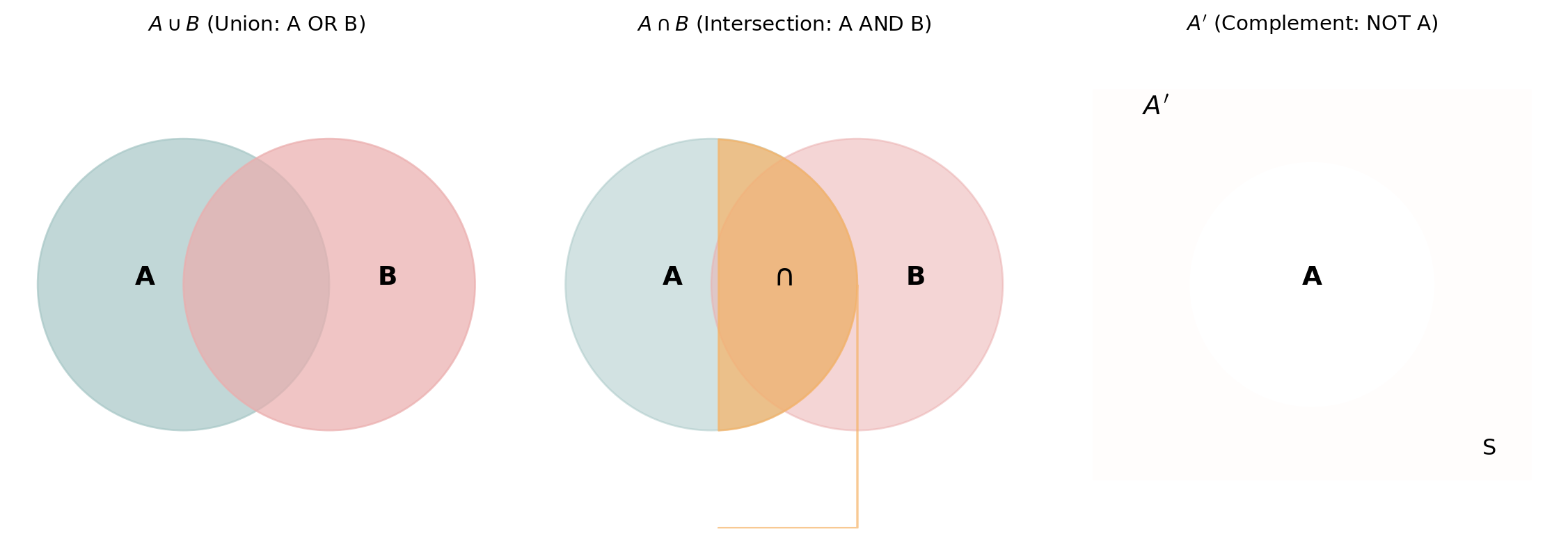
Set Operation Summary

Remember these from the start of the course?

Operation	Notation	Meaning
Union	\(A \cup B\)	A or B (or both)
Intersection	\(A \cap B\)	A and B
Complement	\(A'\) or \(\bar{A}\)	Not A
Set difference	\(A \setminus B\)	A but not B (= \(A \cap B'\))

. . .

\(A \setminus B\) means outcomes that are in \(A\) but excluded from \(B\). In probability, this is often easier to compute as \(P(A) - P(A \cap B)\).

Set Operations on Events

. . .

If visualized, this is not too bad, isn’t it?

Part B: Probability Axioms

Definition of Probability

Kolmogorov Axioms, for any event \(A\):

\(P(A) \geq 0\) (non-negativity)
\(P(S) = 1\) (certainty)
For mutually exclusive events: \(P(A \cup B) = P(A) + P(B)\)

. . .

Consequence: \(0 \leq P(A) \leq 1\) for all events \(A\)

Classical Probability

For equally likely outcomes:

\[P(A) = \frac{\text{Number of favorable outcomes}}{\text{Total number of outcomes}} = \frac{|A|}{|S|}\]

. . .

Example: Rolling a fair die

\[P(\text{even}) = \frac{|\{2, 4, 6\}|}{|\{1,2,3,4,5,6\}|} = \frac{3}{6} = \frac{1}{2}\]

. . .

This is rather intuitive, just imagine playing board games.

Complements

Complement Rule (Gegenwahrscheinlichkeit):

\[P(A') = 1 - P(A)\]

. . .

Example: If probability of rain is 0.3, what is the probability of no rain?

. . .

\[P(\text{no rain}) = 1 - P(\text{rain}) = 1 - 0.3 = 0.7\]

. . .

The complement rule is often useful when it’s easier to calculate what you don’t want!

Example: Using the Complement

A company knows that 5% of its products are defective.

Question: Probability that a random product is NOT defective?

. . .

Solution:

\(P(\text{defective}) = 0.05\)
\(P(\text{not defective}) = 1 - 0.05 = 0.95\)

. . .

Question: In sample of 3 products, what’s the probability that at least one is defective?

. . .

Solution: Use complement! \[P(\text{at least one}) = 1 - P(\text{none defective}) = 1 - (0.95)^3 \approx 0.143\]

Part C: Addition Rule

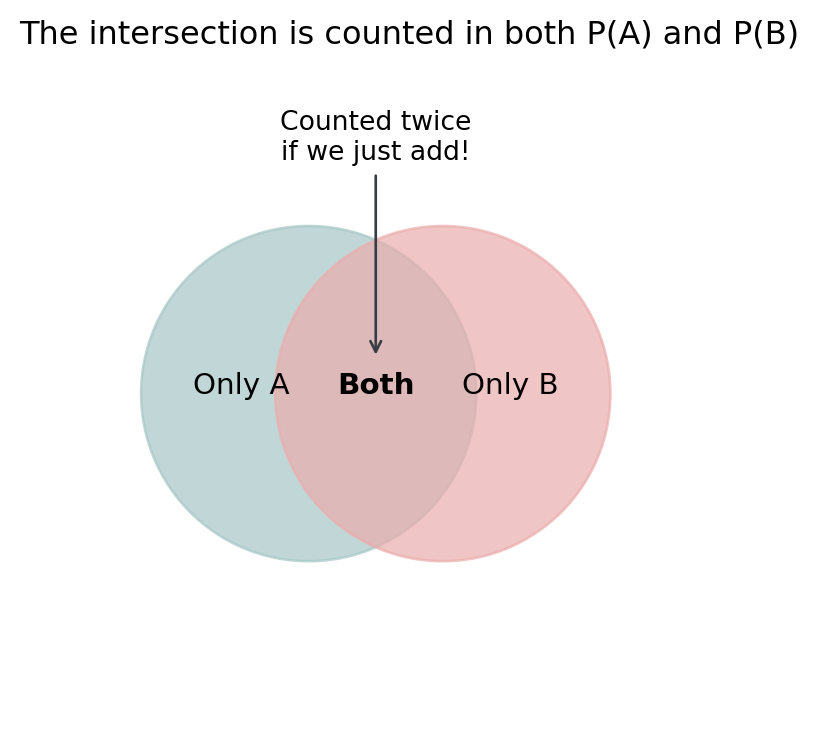
Union of Events

General Addition Rule (Additionssatz)

\[P(A \cup B) = P(A) + P(B) - P(A \cap B)\]

. . .

Why subtract \(P(A \cap B)\)?

Addition Rule Example

In a class of 100 students:

60 study mathematics
40 study economics
25 study both

. . .

Question: What is the probability that a randomly selected student studies mathematics OR economics?

. . .

Solution:

\(P(M \cup E) = P(M) + P(E) - P(M \cap E)\)
\(= 0.60 + 0.40 - 0.25 = 0.75\)

Part D: Mutually Exclusive Events

Disjoint Events

Mutually Exclusive (Disjoint) Events:

Events A and B are mutually exclusive if they cannot occur together:

\[A \cap B = \emptyset \quad \Rightarrow \quad P(A \cap B) = 0\]

. . .

Examples:

Rolling a 3 and rolling a 5 on one die
A product being “good” and “defective”
Being in age group “18-25” and “26-35”

Special Addition Rule

For mutually exclusive events:

\[P(A \cup B) = P(A) + P(B)\]

. . .

Example: Rolling a die, find \(P(\text{1 or 6})\)

. . .

Since rolling 1 and rolling 6 are mutually exclusive:

\[P(1 \cup 6) = P(1) + P(6) = \frac{1}{6} + \frac{1}{6} = \frac{2}{6} = \frac{1}{3}\]

. . .

That’s something we already intuitively knew!

Quick Check - 6 Minutes

Fast Notation Drill

Work individually

Rewrite in symbols: “in A but not in B”.
Compute \(P(A')\) if \(P(A)=0.72\).
If \(P(A)=0.6\), \(P(B)=0.5\), and \(P(A \cap B)=0.2\), compute \(P(A \cup B)\).

Break - 10 Minutes

Part E: Independent Events

Independence

Definition: Independent Events

Events A and B are independent if the occurrence of one does not affect the probability of the other:

\[P(A \cap B) = P(A) \cdot P(B)\]

. . .

Don’t confuse:

Mutually exclusive: Can’t happen together (\(P(A \cap B) = 0\))
Independent: Don’t affect each other (\(P(A \cap B) = P(A) \cdot P(B)\))

Independence Example

Two machines work independently. Machine A has 95% reliability, Machine B has 90% reliability.

. . .

Question: What is the probability both machines work?

. . .

\[P(A \cap B) = P(A) \cdot P(B) = 0.95 \times 0.90 = 0.855\]

. . .

Question: What is the probability at least one machine fails?

. . .

\[P(\text{at least one fails}) = 1 - P(\text{both work}) = 1 - 0.855 = 0.145\]

Mutually Exclusive vs Independent

Property	Mutually Exclusive	Independent
\(P(A \cap B)\)	\(= 0\)	\(= P(A) \cdot P(B)\)
Occur together?	No	Yes
A occurred…	…tells B didn’t	…tells nothing about B
Example	“Pass” vs “Fail”	Two separate coin flips

. . .

If \(P(A) > 0\) and \(P(B) > 0\), then mutually exclusive events cannot be independent!

Quick Check - 6 Minutes

Mutually Exclusive or Independent?

Work individually

Classify each pair as mutually exclusive, independent, both, or neither.

One coin flip: A = “Heads”, B = “Tails”
Two separate coin flips: A = “Heads on flip 1”, B = “Heads on flip 2”
One die roll: A = “even”, B = “greater than 3”

Part F: Business Applications

Quality Control Application

A factory produces items with:

3% have surface defects (event S)
2% have internal defects (event I)
0.5% have both defects

. . .

Find the probability that an item has:

At least one type of defect
A surface defect but no internal defect
Exactly one type of defect

Market Research Application

In a survey of 500 consumers:

300 prefer Brand A
250 prefer organic products
150 prefer Brand A AND organic

. . .

Question: Are “preferring Brand A” and “preferring organic” independent?

Part G: Random Variables, PMF, and CDF

Random Variable (Discrete Case)

Definition: A random variable \(X\) assigns a numerical value to each outcome in the sample space.

. . .

Formally: \(X:S\to\mathbb{R}\).

Example: Number of defective items in a sample
Example: Number shown on a die

. . .

Think of it like a function that takes an outcome and returns a number.

PMF

Definition: Probability Mass Function:

For a discrete random variable \(X\), the PMF is \(p_X(x) = P(X=x)\)
It has the following properties:
- \(p_X(x) \ge 0\)
- \(\sum_x p_X(x)=1\)

. . .

Example: Let \(X\) = number of heads in two fair coin flips.

\(x\)	0	1	2
\(P(X=x)\)	\(\frac14\)	\(\frac12\)	\(\frac14\)

CDF

Definition: Cumulative Distribution Function:

For a random variable \(X\), the CDF is \(F_X(x)=P(X\le x)\)
The CDF adds probabilities up to a threshold.
Interpretation in words: “at most \(x\)”.

. . .

Using the same example:

\(F_X(0)=P(X\le 0)=\frac14\)
\(F_X(1)=P(X\le 1)=\frac14+\frac12=\frac34\)
\(F_X(2)=1\)

PMF vs CDF Quick Comparison

Question	Use	Example result
“Exactly 1 head”	PMF	\(P(X=1)=\frac12\)
“At most 1 head”	CDF	\(P(X\le1)=\frac34\)

. . .

Common exam error: confusing \(P(X=1)\) with \(P(X\le 1)\). Always check whether the wording is “exactly” or “at most”.

Quick Check - 5 Minutes

PMF and CDF Practice

Work individually

Given the PMF:

\(x\)	0	1	2	3
\(P(X=x)\)	0.10	0.35	0.40	0.15

Compute \(P(X\ge2)\).
Compute \(F_X(1)\).
Is \(F_X(1)\) the same as \(P(X=1)\)?

Guided Practice - 20 Minutes

Practice Problems I

Work in pairs

Problem 1: A card is drawn from a standard 52-card deck.

Find \(P(\text{Heart})\)
Find \(P(\text{Face card})\) (J, Q, K)
Find \(P(\text{Heart OR Face card})\)

Problem 2: In a company, 40% of employees are in sales, 30% are in engineering, and 10% are in both. Find:

\(P(\text{Sales OR Engineering})\)
\(P(\text{neither Sales nor Engineering})\)

Practice Problems II

Work in pairs

Problem 3 (Notation Translation):

In a survey, let:

\(T\) = has payback card
\(K\) = active customer this month

Write in words what \(T \setminus K\) means.
Rewrite \(T \setminus K\) using intersection and complement notation.
If \(P(T)=0.62\) and \(P(T \cap K)=0.41\), compute \(P(T \setminus K)\).

Practice Problems III

Work in pairs

Problem 4 (Complements + Wording):

In a support center, 18% of customers submit at least one complaint in a quarter.

What is the probability that a customer submits no complaint?
In words, explain what event is represented by the complement here.
If 500 customers are observed, about how many are expected to submit no complaint?

Chained Exam Mini-Problem

Work individually, then compare

For events \(A\) and \(B\), suppose \(P(A)=0.55\), \(P(B)=0.40\), \(P(A\cap B)=0.18\).

Compute \(P(A\cup B)\).
Use your result from (a) to compute \(P((A\cup B)')\).
Interpret part (b) in plain business language.

Coffee Break - 10 Minutes

Collaborative Problem-Solving - 20 Minutes

Group Challenge: Customer Segments

Think individually then work in groups of 3-4

In a customer base:

\(P(T)=0.58\) (uses app)
\(P(K)=0.47\) (premium member)
\(P(T \cap K)=0.29\)

Compute \(P(T \cup K)\).
Compute \(P(T \setminus K)\) and explain it in words.
Check whether \(T\) and \(K\) are independent.
Write one business recommendation based on your result.

Sample Space and Events: Product Returns

Work in pairs

An online shop classifies returns by reason: Defective (D), Wrong Size (S), Changed Mind (M), or Other (O).

Write the sample space \(\Omega\) for the reason of a single return.
Define event \(A\) = “return is the customer’s fault” and list its outcomes.
Write \(A'\) in words and list its outcomes.
If \(P(D)=0.15\), \(P(S)=0.40\), \(P(M)=0.30\), find \(P(O)\) using the axioms.

Complement and Addition Rule: Delivery Service

Work individually

A logistics company tracks two events for its deliveries:

\(L\) = “delivery is late”, with \(P(L)=0.12\)
\(D\) = “package is damaged”, with \(P(D)=0.05\)
\(P(L \cap D)=0.02\)

Find \(P(L \cup D)\) and interpret it in words.
Find \(P(L')\) and interpret it.
Find \(P(L \setminus D)\). What does this represent?
Are \(L\) and \(D\) mutually exclusive? Are they independent?

Independence: Machine Failures

Work in pairs

A factory has two machines, A and B, that operate independently.

\(P(\text{A fails}) = 0.08\)
\(P(\text{B fails}) = 0.05\)

What is the probability that both machines fail?
What is the probability that at least one machine fails?
What is the probability that exactly one machine fails?
The factory shuts down only if both machines fail. What is the probability that the factory keeps running?

PMF and CDF: Customer Orders

Work individually, then compare

Let \(X\) be the number of items in a random online order. The PMF is:

\(x\)	1	2	3	4	5
\(P(X=x)\)	0.30	0.25	0.20	0.15	0.10

Verify this is a valid PMF.
Compute \(F_X(3) = P(X \le 3)\).
Compute \(P(X > 3)\) using the CDF.
Compute \(P(2 \le X \le 4)\).

Mixed Problem: Marketing Campaign

Work in groups

A marketing team surveys 200 customers. Let \(E\) = “opened the email” and \(C\) = “clicked the link”.

120 opened the email
50 clicked the link
40 both opened the email and clicked the link

Find \(P(E)\), \(P(C)\), and \(P(E \cap C)\).
Find \(P(E \cup C)\) and interpret it.
Are \(E\) and \(C\) independent? Show your work.
Define a random variable \(X\) = “number of actions taken” (opening counts as one action, clicking counts as another). Write the PMF of \(X\).

Final Assessment - 5 Minutes

Exit Ticket

Work individually, then compare

If \(P(A)=0.55\), what is \(P(A')\)?
If \(P(A)=0.40\), \(P(B)=0.35\), and \(P(A \cap B)=0.12\), find \(P(A \cup B)\).
In words, what does \(A \setminus B\) mean?

Wrap-Up & Key Takeaways

Today’s Essential Concepts

Sample space \(S\): All possible outcomes
Event: Subset of the sample space
Probability axioms: \(0 \leq P(A) \leq 1\), \(P(S) = 1\)
Complement: \(P(A') = 1 - P(A)\)
Addition rule: \(P(A \cup B) = P(A) + P(B) - P(A \cap B)\)
Mutually exclusive: \(P(A \cap B) = 0\)
Independent: \(P(A \cap B) = P(A) \cdot P(B)\)
Random variables: PMF for exact values, CDF for cumulative values

Next Session Preview

Coming Up: Combinatorics

Fundamental counting principle
Permutations: arrangements where order matters
Combinations: selections where order doesn’t matter
Applications to probability calculations

. . .

Homework

Complete Tasks 07-02:

Practice sample space identification
Apply probability rules
Solve business probability problems