Session 07-05 - Bayes’ Theorem
Section 07: Probability & Statistics
Entry Quiz - 10 Minutes
Quick Review from Session 07-04
If \(P(A) = 0.5\), \(P(B) = 0.4\), and \(P(A \cap B) = 0.2\), find \(P(A|B)\).
A bag has 4 red and 6 blue balls. Two are drawn without replacement. Find \(P(\text{both blue})\).
Given \(P(B|A) = 0.6\) and \(P(A) = 0.3\), find \(P(A \cap B)\).
If \(P(A|B) = P(A)\), what can we conclude about A and B?
Learning Objectives
What You’ll Master Today
- Apply Bayes’ Theorem: \(P(A|B) = \frac{P(B|A) \cdot P(A)}{P(B)}\)
- Understand prior and posterior probabilities
- Calculate sensitivity and specificity for diagnostic tests
- Compute PPV and NPV (positive/negative predictive values)
- Solve medical testing problems - a key exam topic!
. . .
Bayes’ Theorem appears on virtually every Feststellungsprüfung!
Part A: Bayes’ Theorem
Reversing Conditional Probabilities
The problem: We often know \(P(B|A)\) but need \(P(A|B)\).
. . .
Example: - We know \(P(\text{positive test}|\text{disease})\) (sensitivity) - We need \(P(\text{disease}|\text{positive test})\) (PPV)
. . .
These are not the same! This is a common misconception.
Bayes’ Theorem Formula
ImportantBayes’ Theorem (Satz von Bayes)
\[P(A|B) = \frac{P(B|A) \cdot P(A)}{P(B)}\]
Using the law of total probability:
\[P(A|B) = \frac{P(B|A) \cdot P(A)}{P(B|A) \cdot P(A) + P(B|A') \cdot P(A')}\]
Understanding the Components
| Term | Name | Meaning |
|---|---|---|
| \(P(A)\) | Prior | Initial probability before evidence |
| \(P(A\|B)\) | Posterior | Updated probability after evidence |
| \(P(B\|A)\) | Likelihood | How likely is evidence given A? |
| \(P(B)\) | Evidence | Total probability of evidence |
. . .
\[\text{Posterior} = \frac{\text{Likelihood} \times \text{Prior}}{\text{Evidence}}\]
Part B: Medical Testing Framework
Key Terminology
ImportantMedical Test Metrics
| Metric | Formula | Meaning |
|---|---|---|
| Sensitivity | \(P(+\|D)\) | Correctly identifies sick people |
| Specificity | \(P(-\|D')\) | Correctly identifies healthy people |
| Prevalence | \(P(D)\) | Proportion with disease in population |
| PPV | \(P(D\|+)\) | Probability of disease given positive test |
| NPV | \(P(D'\|-)\) | Probability of no disease given negative test |
The 2×2 Table
| Disease (+) | No Disease (−) | Total | |
|---|---|---|---|
| Test + | True Positive (TP) | False Positive (FP) | Test + |
| Test − | False Negative (FN) | True Negative (TN) | Test − |
| Total | Disease | No Disease | Population |
. . .
- Sensitivity = \(\frac{TP}{TP + FN}\)
- Specificity = \(\frac{TN}{TN + FP}\)
- PPV = \(\frac{TP}{TP + FP}\)
- NPV = \(\frac{TN}{TN + FN}\)
Example: COVID Test
A rapid COVID test has:
- Sensitivity: 95% (correctly identifies 95% of infected people)
- Specificity: 98% (correctly identifies 98% of healthy people)
- Prevalence: 2% (2% of population currently infected)
. . .
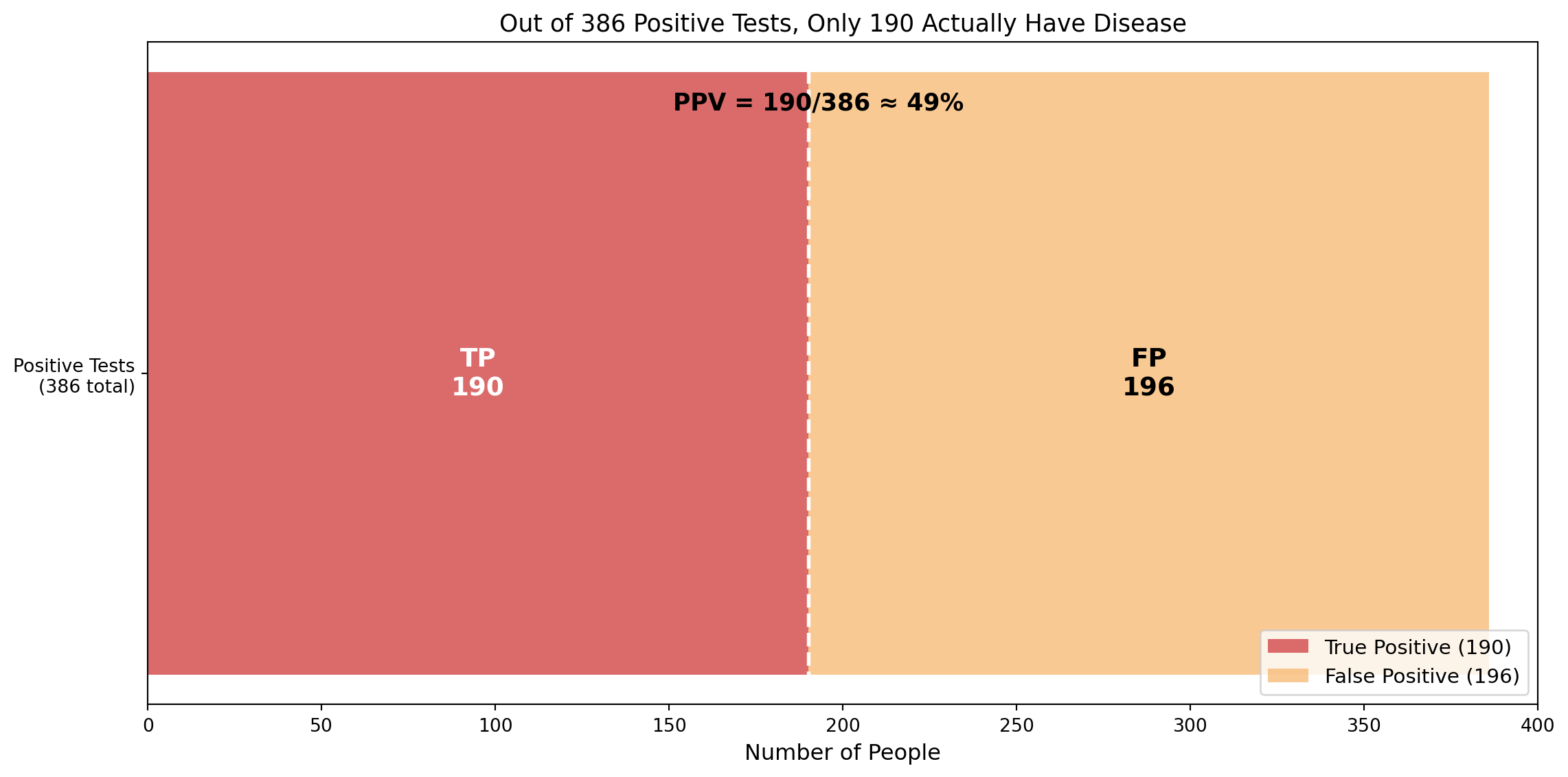
Question: If you test positive, what’s the probability you actually have COVID?
. . .
This is asking for PPV = \(P(D|+)\)!
Solution Using Bayes’ Theorem
\[P(D|+) = \frac{P(+|D) \cdot P(D)}{P(+)}\]
. . .
Calculate \(P(+)\) using law of total probability: \[P(+) = P(+|D) \cdot P(D) + P(+|D') \cdot P(D')\] \[= 0.95 \times 0.02 + 0.02 \times 0.98 = 0.019 + 0.0196 = 0.0386\]
. . .
Apply Bayes: \[P(D|+) = \frac{0.95 \times 0.02}{0.0386} = \frac{0.019}{0.0386} \approx 0.492\]
. . .
Only about 49% of positive tests are true positives when prevalence is low!
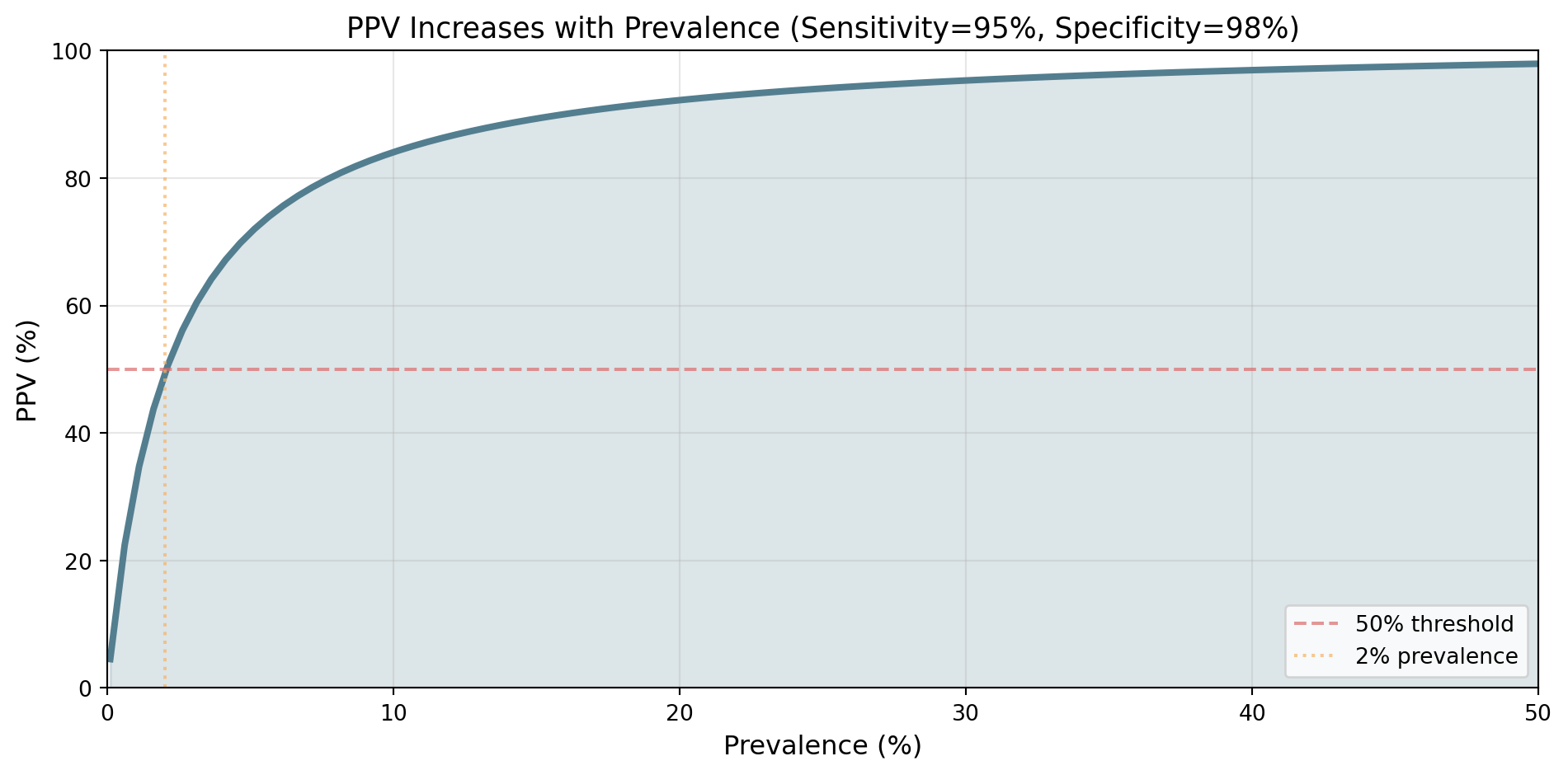
Visual: Why PPV Can Be Low
The Prevalence Effect
. . .
PPV depends heavily on prevalence!
Break - 10 Minutes
Part C: Systematic Problem-Solving
Step-by-Step Approach
TipStrategy for Bayes Problems
- Identify what you need: Usually \(P(D|+)\) or \(P(D|-)\)
- Extract given information: Sensitivity, specificity, prevalence
- Set up the formula: Write Bayes’ theorem
- Calculate \(P(+)\) or \(P(-)\): Use law of total probability
- Substitute and solve: Careful with arithmetic!
- Interpret: What does the answer mean?
Complete Example: Disease Screening
A screening test for a disease has:
- Sensitivity = 90%
- Specificity = 95%
- Prevalence = 1%
Find: a) PPV b) NPV
Solution Part a) PPV
\[P(D|+) = \frac{P(+|D) \cdot P(D)}{P(+|D) \cdot P(D) + P(+|D') \cdot P(D')}\]
. . .
Given values: - \(P(+|D) = 0.90\) (sensitivity) - \(P(D) = 0.01\) (prevalence) - \(P(+|D') = 1 - 0.95 = 0.05\) (false positive rate) - \(P(D') = 0.99\)
. . .
\[P(D|+) = \frac{0.90 \times 0.01}{0.90 \times 0.01 + 0.05 \times 0.99}\] \[= \frac{0.009}{0.009 + 0.0495} = \frac{0.009}{0.0585} \approx 0.154\]
Solution Part b) NPV
\[P(D'|-) = \frac{P(-|D') \cdot P(D')}{P(-)}\]
. . .
Calculate \(P(-)\): \[P(-) = P(-|D) \cdot P(D) + P(-|D') \cdot P(D')\] \[= 0.10 \times 0.01 + 0.95 \times 0.99 = 0.001 + 0.9405 = 0.9415\]
. . .
\[P(D'|-) = \frac{0.95 \times 0.99}{0.9415} = \frac{0.9405}{0.9415} \approx 0.999\]
. . .
PPV is only 15.4%, but NPV is 99.9%! A negative result is very reliable.
Part D: Contingency Table Method
Alternative Approach
Use a hypothetical population (e.g., 10,000 people):
| Disease | No Disease | Total | |
|---|---|---|---|
| Test + | |||
| Test − | |||
| Total | 100 | 9,900 | 10,000 |
. . .
Fill in using sensitivity and specificity:
| Disease | No Disease | Total | |
|---|---|---|---|
| Test + | 90 | 495 | 585 |
| Test − | 10 | 9,405 | 9,415 |
| Total | 100 | 9,900 | 10,000 |
. . .
Read directly: PPV = \(\frac{90}{585} = 0.154\), NPV = \(\frac{9405}{9415} = 0.999\)
Guided Practice - 20 Minutes
Practice Problem 1
A factory has two machines:
- Machine A produces 60% of items, with 3% defect rate
- Machine B produces 40% of items, with 5% defect rate
If a randomly selected item is defective, what’s the probability it came from Machine A?
Practice Problem 2 (Exam-Style)
A medical test has sensitivity 85% and specificity 90%.
In a population with 5% prevalence:
- Calculate PPV
- Calculate NPV
- Construct a contingency table for 1000 people
- Interpret your results
Wrap-Up & Key Takeaways
Today’s Essential Concepts
- Bayes’ Theorem: \(P(A|B) = \frac{P(B|A) \cdot P(A)}{P(B)}\)
- Medical testing: Sensitivity, specificity, prevalence
- PPV and NPV: What positive/negative results mean
- Prevalence matters: Low prevalence → Low PPV
- Two methods: Formula or contingency table
Next Session Preview
Coming Up: Contingency Tables
- Constructing tables from word problems
- Reading marginal, joint, and conditional probabilities
- Independence testing in tables
- Exam-style problems
. . .
TipHomework
Complete Tasks 07-05 - especially the medical testing problems!