Part 1: Function Fundamentals

What is a Function?

Definition: A function is a special relationship between two sets where each element in the domain (input set) is paired with exactly one element in the range (output set).

Think of a function as a machine: you put something in (input), and it gives you exactly one thing out (output). You can’t get two different outputs for the same input!

Function Notation and Terminology

Let’s explore the language of functions:

Symbol/Term	Name	Meaning
\(f, g, h\)	Function names	Letters used to identify different functions
\(D_f\)	Domain	The set of all possible input values (\(x\)-values)
\(W_f\) or \(R_f\)	Range	The set of all possible output values (\(y\)-values)
\(f(x_0)\)	Function value	The output when \(x_0\) is the input
\(f: x \rightarrow 3x^2 + 5\)	Function rule	The recipe that transforms inputs to outputs
\(f(x) = 3x^2 + 5\)	Function equation	The formula for calculating outputs

Example: Understanding Function Notation

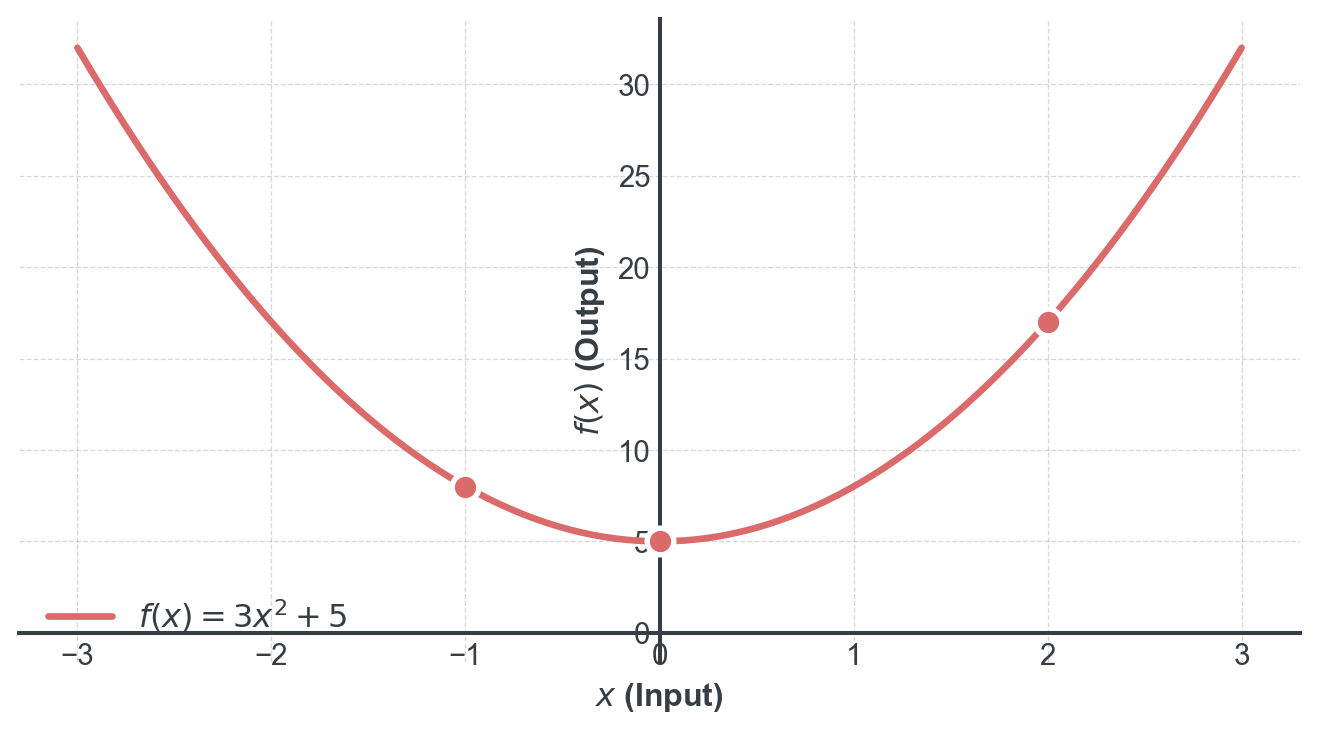
Consider the function \(f(x) = 3x^2 + 5\)

Function rule: \(f: x \rightarrow 3x^2 + 5\)

This tells us: “Take any number \(x\), square it, multiply by 3, then add 5”

Calculating function values:

When \(x = 2\): \(f(2) = 3 \cdot 2^2 + 5 = 3 \cdot 4 + 5 = 17\)
When \(x = -1\): \(f(-1) = 3 \cdot (-1)^2 + 5 = 3 \cdot 1 + 5 = 8\)
When \(x = 0\): \(f(0) = 3 \cdot 0^2 + 5 = 5\)

Part 2: Visualizing Functions

Let’s see what this function looks like!

Key Observation:

Notice that for every \(x\)-value, there is exactly one \(y\)-value. This is what makes it a function!

Part 3: Domain and Range Notation

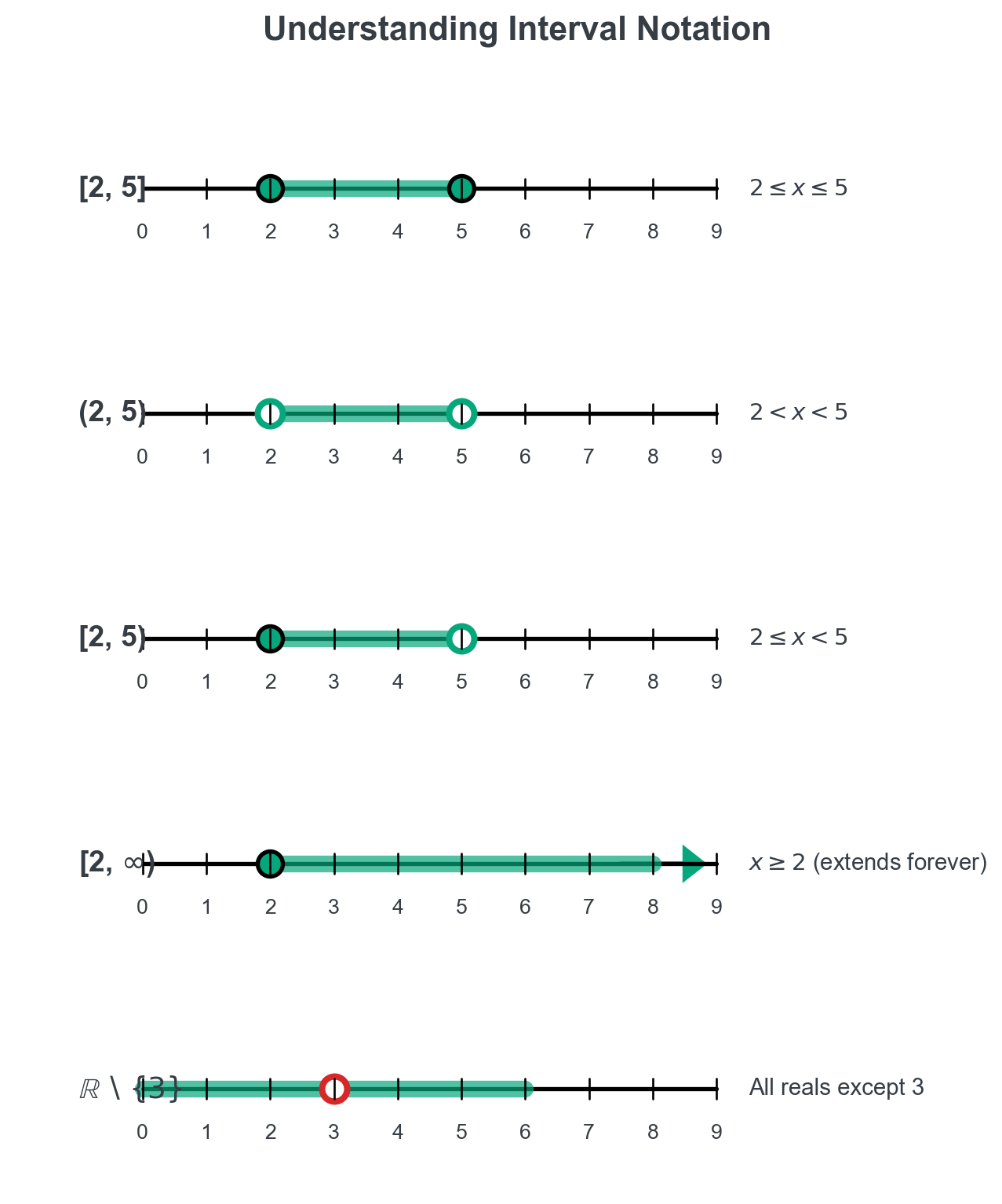
When describing domains and ranges, we use interval notation:

Notation	Meaning	Description
\([a, b]\)	\(a \leq x \leq b\)	Closed interval (includes both endpoints)
\((a, b)\)	\(a < x < b\)	Open interval (excludes both endpoints)
\([a, b)\)	\(a \leq x < b\)	Half-open interval (includes \(a\), excludes \(b\))
\([a, \infty)\)	\(x \geq a\)	All real numbers greater than or equal to \(a\)
\(\mathbb{R} \setminus \{a\}\)	All reals except \(a\)	The real numbers with \(a\) removed
\(\mathbb{R}^+\)	\(x > 0\)	All positive real numbers

Visual Examples

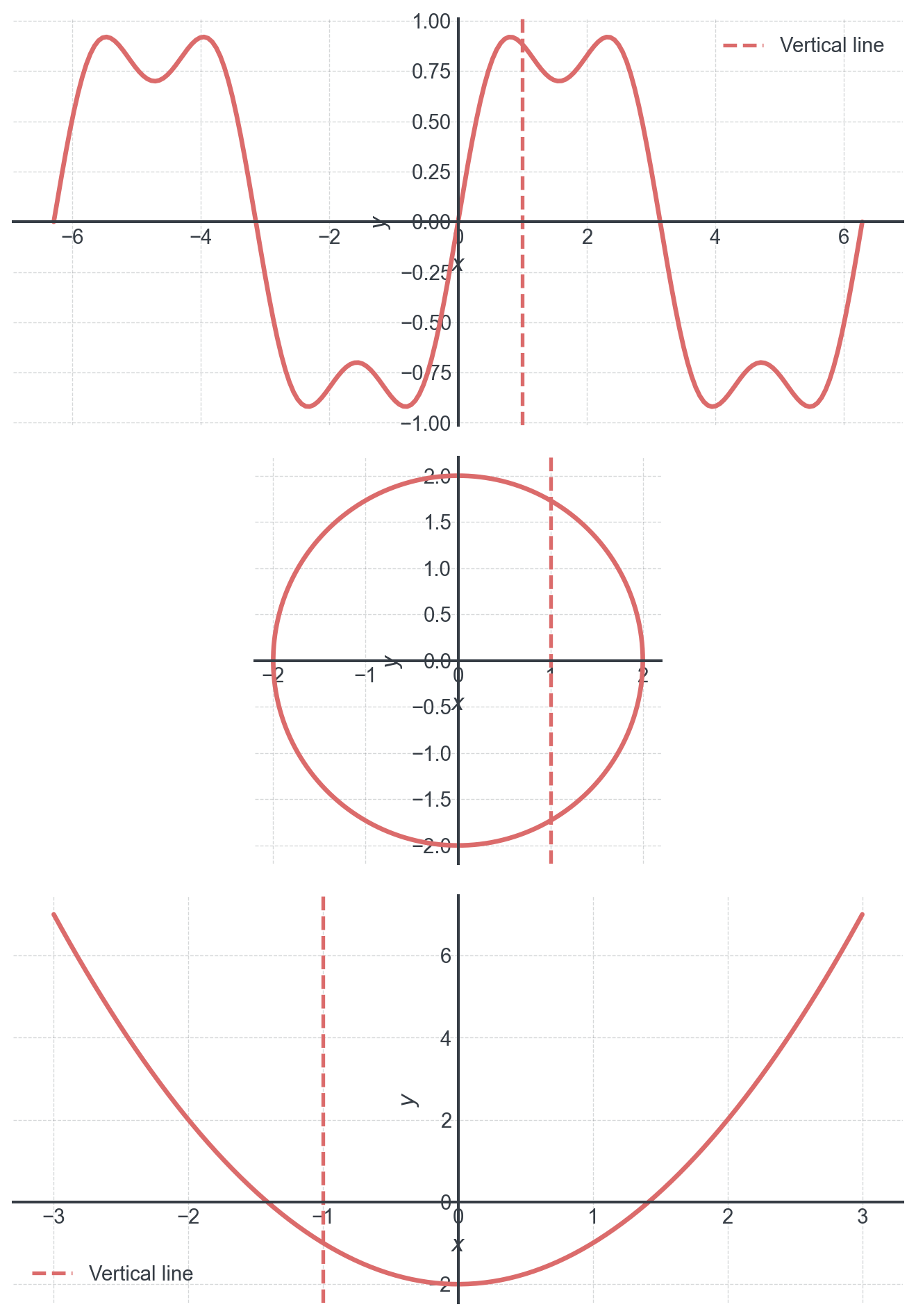
Figure 2: Visual representation of interval notation

Part 4: The Vertical Line Test

How to Identify a Function from its Graph

The Vertical Line Test: A graph represents a function if and only if no vertical line intersects the graph more than once.

Why does this work?

Remember: A function assigns exactly one output to each input. A vertical line represents all points with the same \(x\)-value (input). If it hits the graph twice, that means one input has two different outputs — not a function!

Figure 3: The Vertical Line Test in action

Part 5: Practice Exercises

Exercise 1: Identify Functions from Graphs

For each graph below, determine whether it represents a function. Explain your reasoning using the vertical line test.

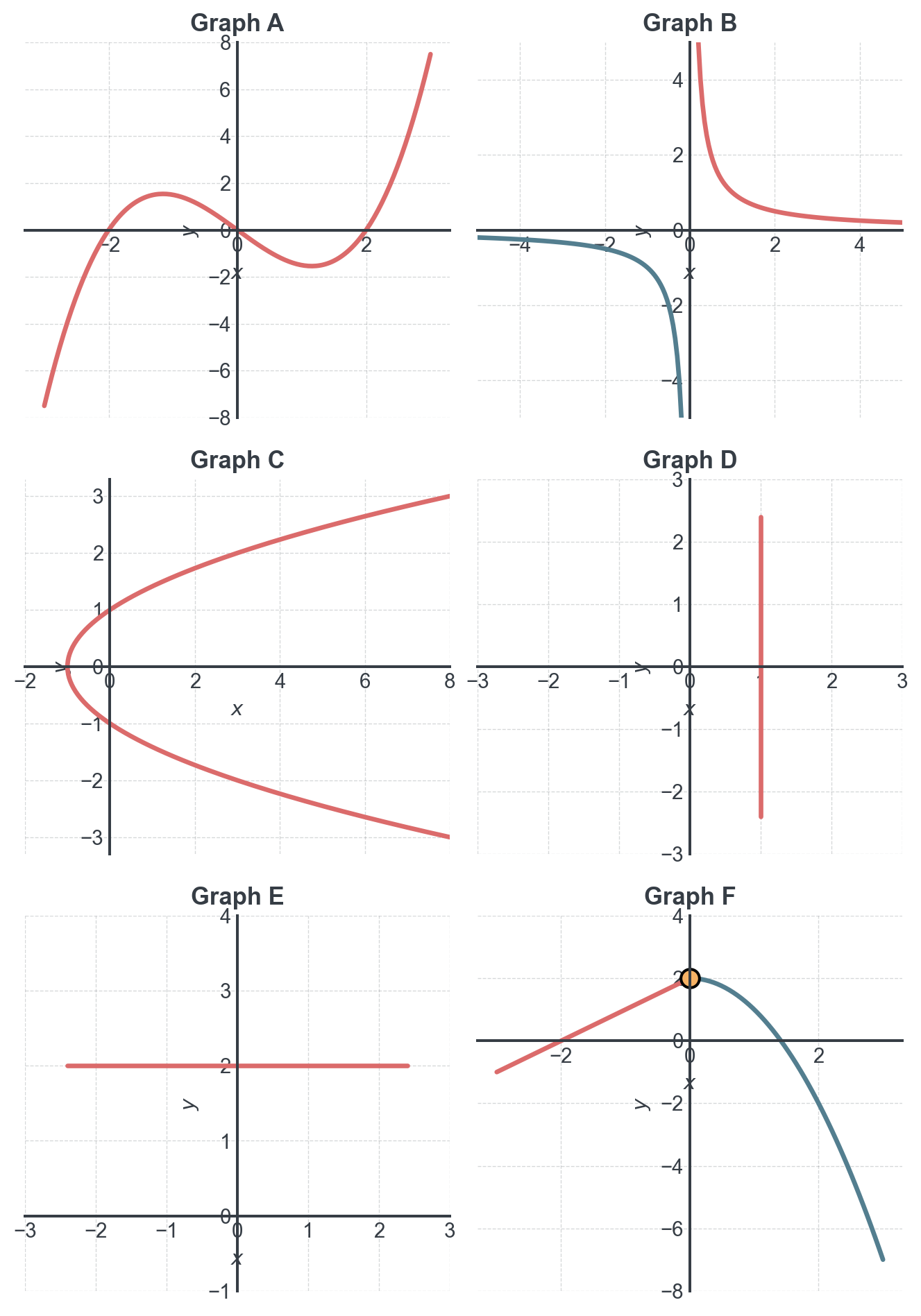
Figure 4: Which of these graphs represent functions?

Your answers:

Graph	Function? (Yes/No)	Explanation
A
B
C
D
E
F

Exercise 2: Finding Domain and Range

For each function below, determine the domain (\(D_f\)) and range (\(W_f\)). Write your answers using interval notation.

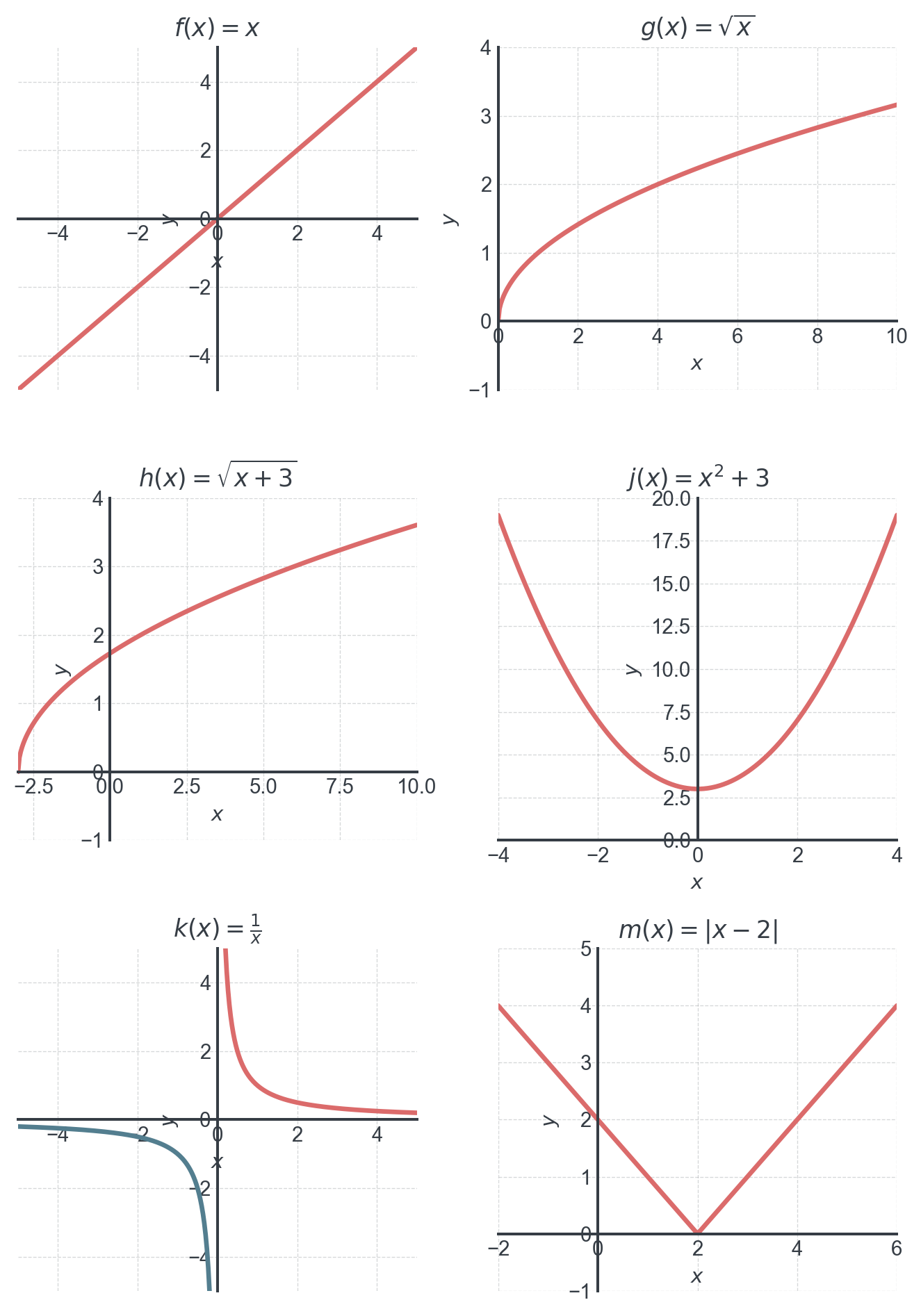
Figure 5: Find the domain and range of these functions

Complete the table:

Function	Domain \(D_f\)	Range \(W_f\)
\(f(x) = x\)
\(g(x) = \sqrt{x}\)
\(h(x) = \sqrt{x + 3}\)
\(j(x) = x^2 + 3\)
\(k(x) = \frac{1}{x}\)
\(m(x) = \\|x - 2\\|\)

Challenge Problems

Challenge 1: Analyzing a Complex Function

Consider the piecewise function:

\[ f(x) = \begin{cases} x + 2 & \text{if } x < 0 \\ x^2 & \text{if } 0 \leq x < 2 \\ 4 & \text{if } x \geq 2 \end{cases} \]

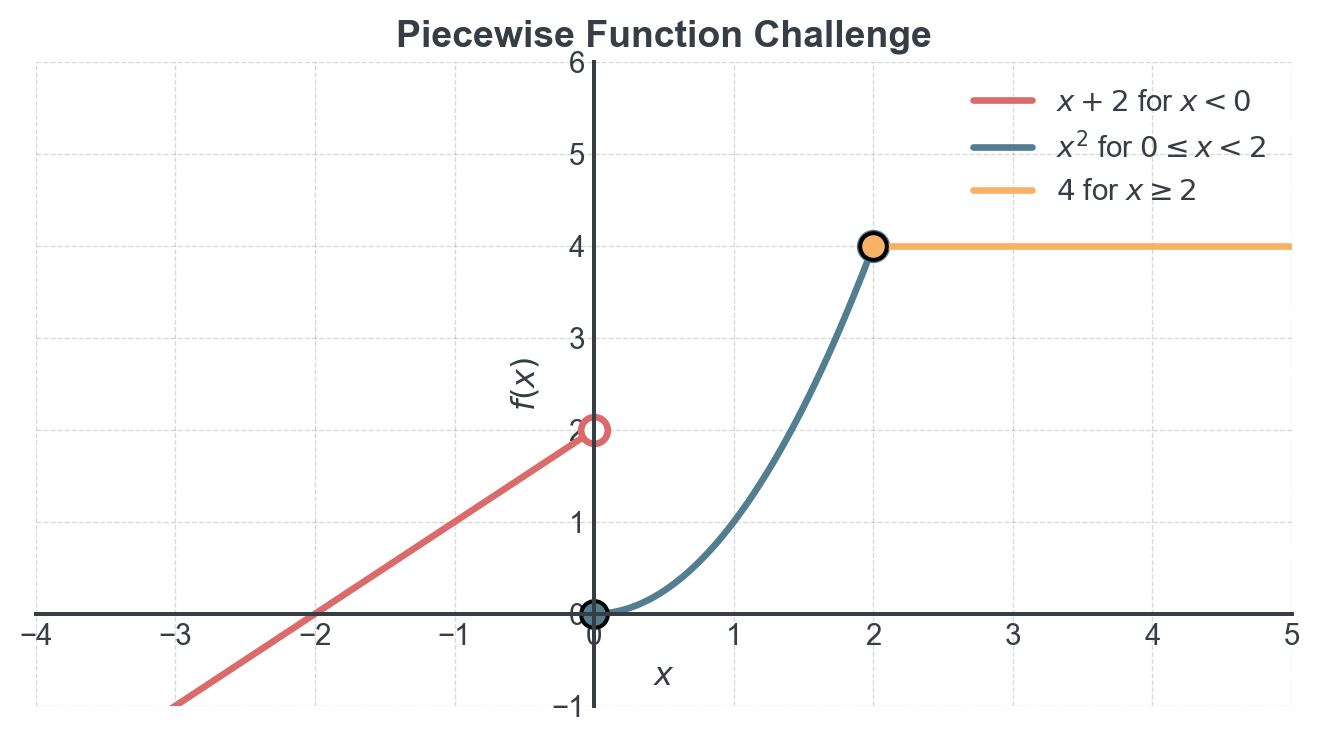
Figure 6: A piecewise function for analysis

Questions:

What is the domain of \(f\)?
What is the range of \(f\)?
Calculate: \(f(-2)\), \(f(0)\), \(f(1)\), \(f(2)\), \(f(3)\)
Is this function continuous? Explain your answer.

Challenge 2: Real-World Application

A delivery company charges based on package weight according to this rule:

\[ C(w) = \begin{cases} 5 & \text{if } 0 < w \leq 1 \\ 5 + 3(w-1) & \text{if } 1 < w \leq 5 \\ 17 + 5(w-5) & \text{if } w > 5 \end{cases} \]

where \(C\) is the cost in dollars and \(w\) is the weight in pounds.

Questions:

How much does it cost to ship a 0.5 lb package?
How much does it cost to ship a 3 lb package?
How much does it cost to ship a 7 lb package?
What is the domain of this function in the real-world context?
Sketch a graph of this function for \(0 < w \leq 10\).

Summary Checklist

Before you finish, make sure you can:

Define what makes a relation a function
Use function notation correctly: \(f(x)\), \(D_f\), \(W_f\)
Write domains and ranges using interval notation
Apply the vertical line test to graphs
Identify functions and non-functions from visual representations
Calculate function values for given inputs
Understand the relationship between a function’s equation and its graph

Answers

Exercise 1: Functions from Graphs

Graph	Function?	Explanation
A	Yes	Any vertical line crosses the graph only once
B	Yes	Any vertical line crosses each branch only once (asymptote at \(x=0\))
C	No	A vertical line at \(x = 2\) intersects the graph twice
D	No	This IS a vertical line, so it has infinite \(y\)-values for one \(x\)-value
E	Yes	Every \(x\)-value has exactly one \(y\)-value (which is 2)
F	Yes	Each piece passes the vertical line test, and they connect properly

Exercise 2: Domain and Range

Function	Domain \(D_f\)	Range \(W_f\)
\(f(x) = x\)	\(\mathbb{R}\) or \((-\infty, \infty)\)	\(\mathbb{R}\) or \((-\infty, \infty)\)
\(g(x) = \sqrt{x}\)	\([0, \infty)\)	\([0, \infty)\)
\(h(x) = \sqrt{x + 3}\)	\([-3, \infty)\)	\([0, \infty)\)
\(j(x) = x^2 + 3\)	\(\mathbb{R}\) or \((-\infty, \infty)\)	\([3, \infty)\)
\(k(x) = \frac{1}{x}\)	\(\mathbb{R} \setminus \{0\}\) or \((-\infty,0) \cup (0,\infty)\)	\(\mathbb{R} \setminus \{0\}\) or \((-\infty,0) \cup (0,\infty)\)
\(m(x) = \\|x - 2\\|\)	\(\mathbb{R}\) or \((-\infty, \infty)\)	\([0, \infty)\)

Great work! You’ve completed the Functions and Their Representations worksheet!