Session 05-01 - Limits & Continuity Through Graphs

Section 05: Differential Calculus

Author

Dr. Nikolai Heinrichs & Dr. Tobias Vlćek

Entry Quiz - 10 Minutes

Quick Review from Section 04

Test your understanding from Advanced Functions

What happens to \(f(x) = \frac{1}{x-2}\) as \(x\) approaches 2 from the right?
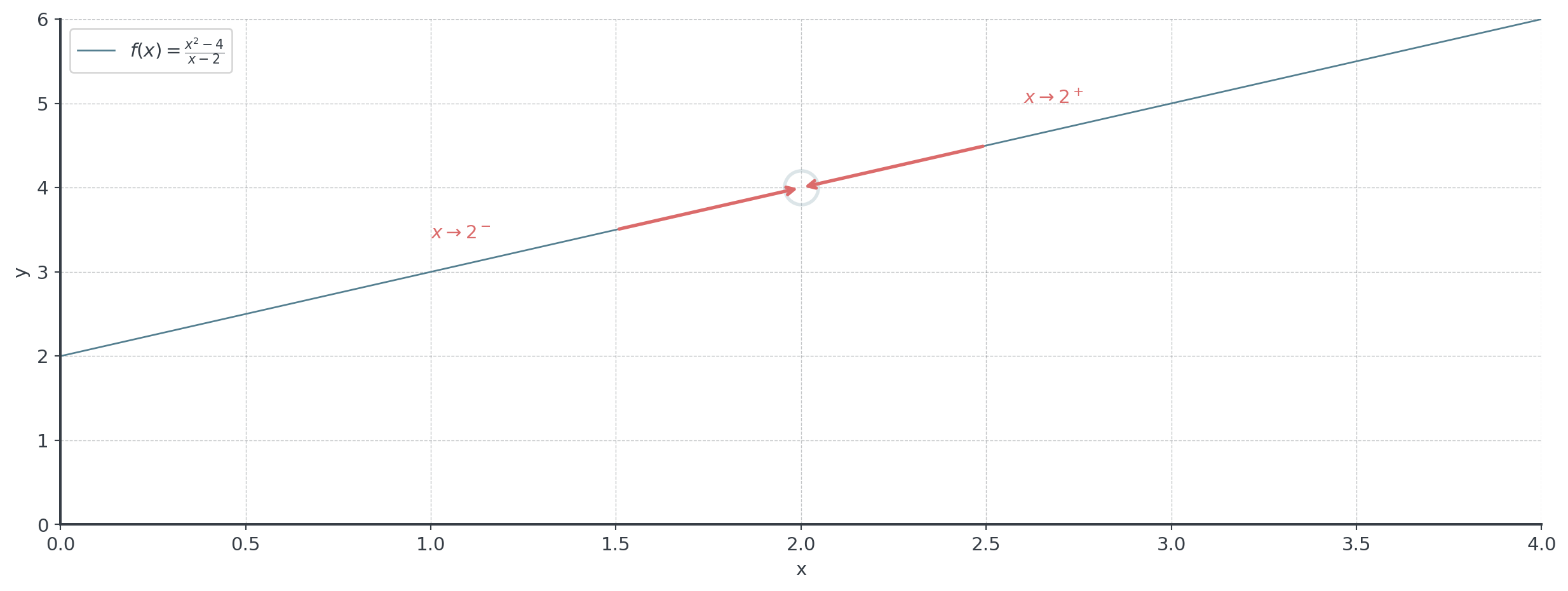
For the rational function \(g(x) = \frac{x^2-4}{x-2}\), what type of discontinuity occurs at \(x = 2\)?
What is the horizontal asymptote of \(f(x) = \frac{3x^2 + 1}{x^2 - 4}\)?

Homework Discussion - 15 Minutes

Your questions from Section 04

Focus on rational functions and asymptotic behavior

Challenges with finding asymptotes of rational functions
Interpreting end behavior and horizontal asymptotes
Understanding vertical asymptotes and domain restrictions
Questions about transformations of functions

. . .

Today we formalize the “limit” concept that explains all this asymptotic behavior!

Learning Objectives

What You’ll Master Today

Understand limits intuitively through graphical analysis
Evaluate one-sided limits and determine when limits exist
Identify types of discontinuities in real-world functions
Apply continuity concepts to business scenarios
Connect abstract math to practical decision-making
Build the foundation for derivatives in the next session

. . .

Limits are the foundation of calculus!

Part A: The Intuitive Limit Concept

From Asymptotes to Limits

Remember rational functions from Section 04?

You saw that \(f(x) = \frac{1}{x}\) gets closer to 0 as \(x\) gets larger
You identified vertical asymptotes where functions “blow up”
You found horizontal asymptotes showing long-term behavior

. . .

Today’s Concept: A limit describes what value a function approaches as the input approaches a specific value.

. . .

Notation: \(\lim_{x \to a} f(x) = L\)

“The limit of \(f(x)\) as \(x\) approaches \(a\) is \(L\)”

Visual Understanding of Limits

We write: \(\lim_{x \to 2} f(x) = 4\)

Look at the Following

. . .

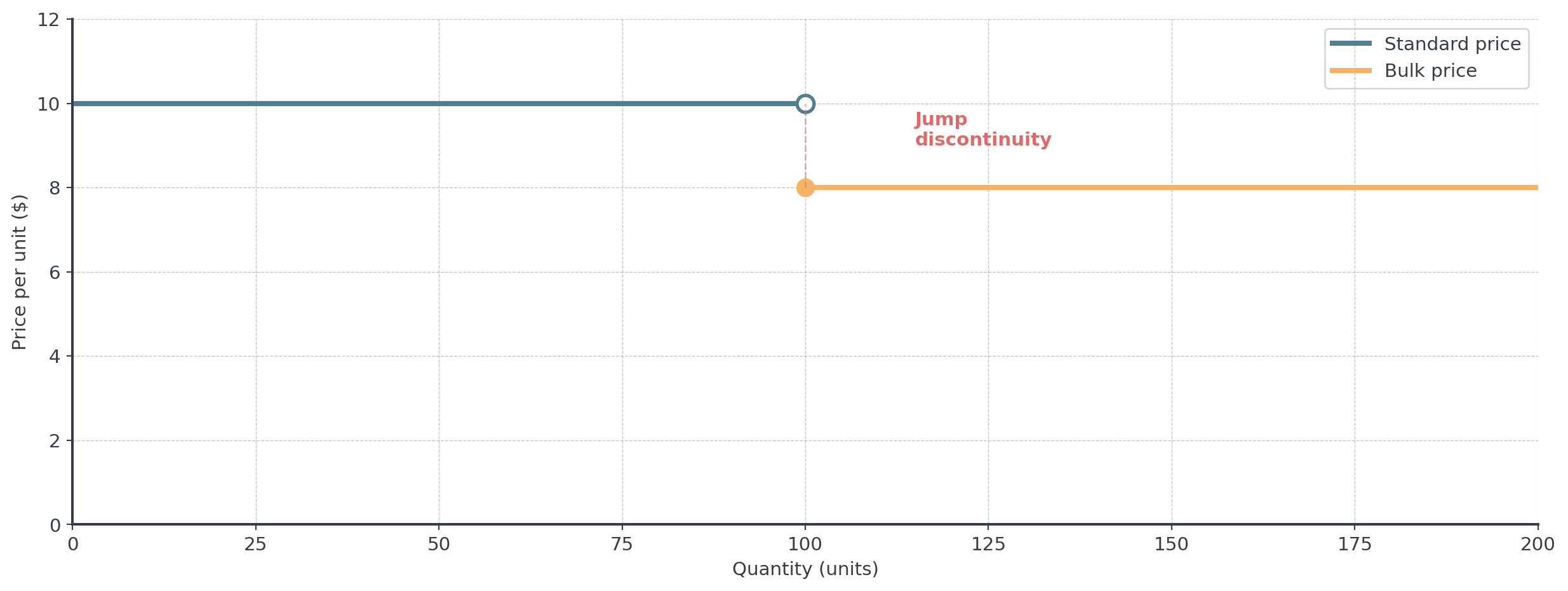
Question: What happens to the price as quantity approaches 100?

Part B: One-Sided Limits

Approaching from Different Directions

Sometimes the approach direction matters!

Left-hand limit: \(\lim_{x \to a^-} f(x)\) (approaching from the left)
Right-hand limit: \(\lim_{x \to a^+} f(x)\) (approaching from the right)
Two-sided limit exists when: Left limit = Right limit

. . .

One-sided limits (like \(\lim_{x \to a^-} f(x)\)) always describe approaching from one direction!

Example: Tax Brackets

This is how taxes are often handled:

. . .

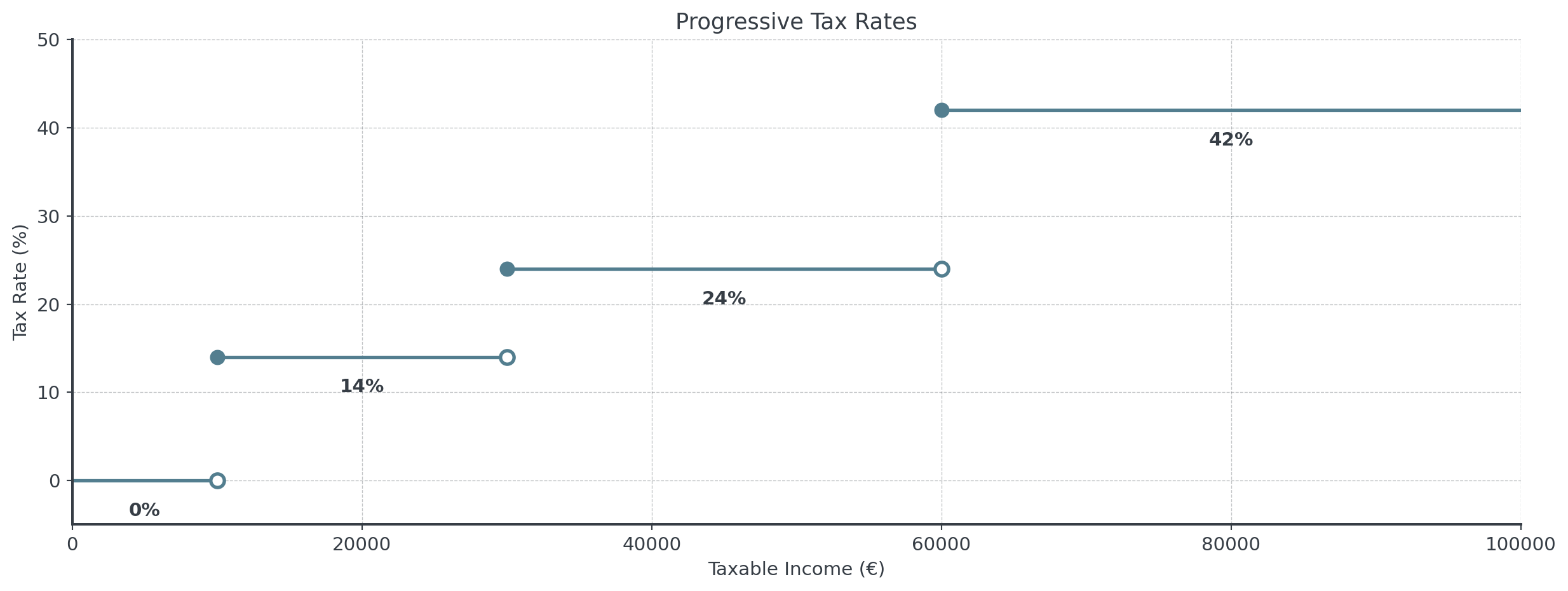
Marginal tax rates, not the effective rate on total income.

Evaluating One-Sided Limits

For the tax function at €30,000:

From the left: \(\lim_{x \to 30000^-} T(x) = 14\%\)
- Income of €29,999 → 14% rate
- Income of €29,999.99 → 14% rate
From the right: \(\lim_{x \to 30000^+} T(x) = 24\%\)
- Income of €30,001 → 24% rate
- Income of €30,000.01 → 24% rate
Two-Sided limit doesn’t exist at €30,000 (jump discontinuity)

Part C: When Limits Exist

Criterion for Two-Sided Limits

A two-sided limit \(\lim_{x \to a} f(x)\) exists if and only if:

The left-hand limit exists: \(\lim_{x \to a^-} f(x) = L_1\)
The right-hand limit exists: \(\lim_{x \to a^+} f(x) = L_2\)
They are equal: \(L_1 = L_2\)
The slope of line approaches the same value from both sides

. . .

Two-sided limits (written simply as \(\lim_{x \to a} f(x)\)) require agreement from both sides. When we say “the limit doesn’t exist,” we typically mean the two-sided limit.

. . .

The limit describes approaching behavior, not the actual value at the point.

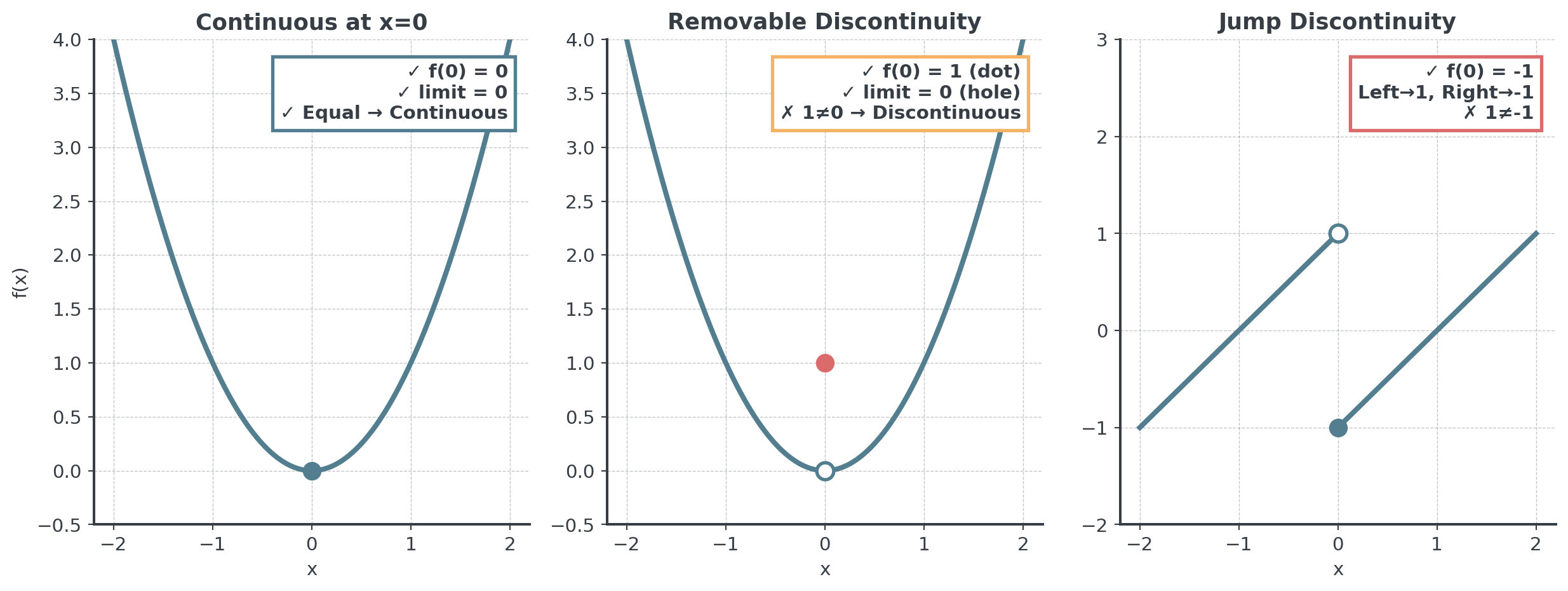
Types: Limit Exists

. . .

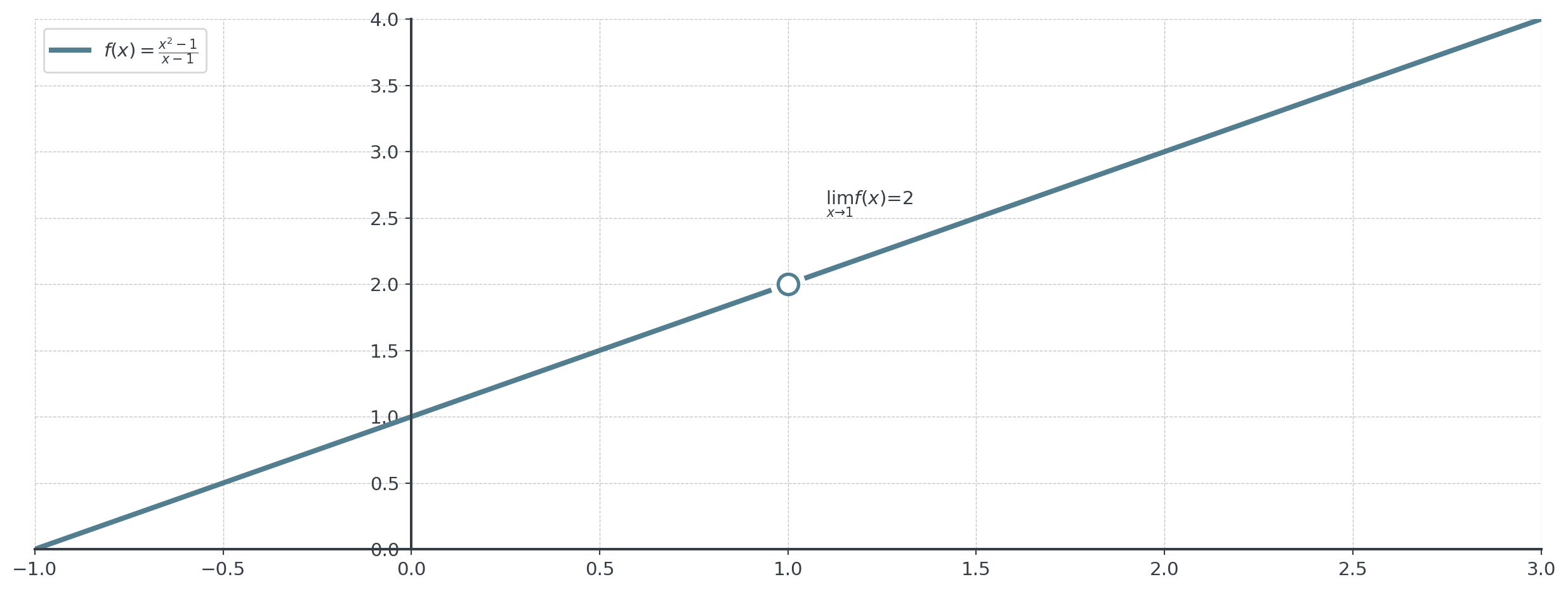
\(\lim_{x \to 1} f(x) = 2\) (even though \(f(1)\) is undefined)

Types: Jump Discontinuity

. . .

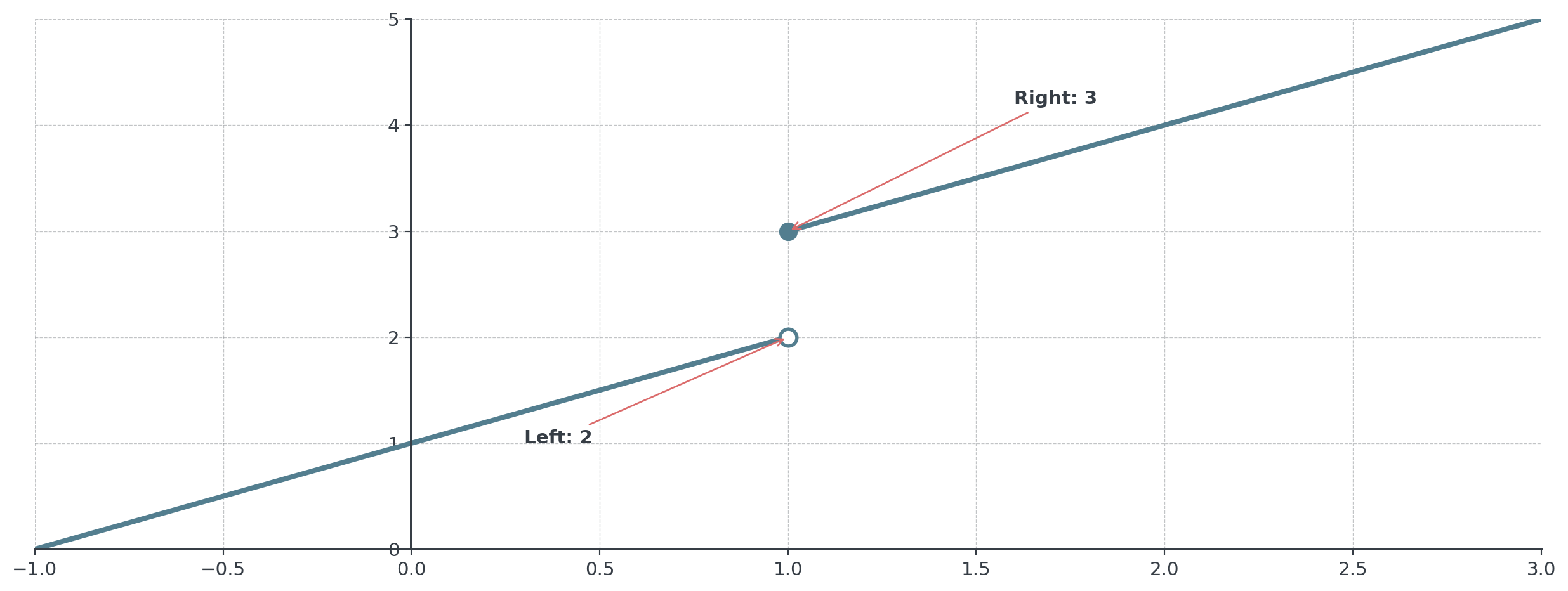
Left limit ≠ Right limit, so limit doesn’t exist (two-sided!)

Types: Infinite Discontinuity

. . .

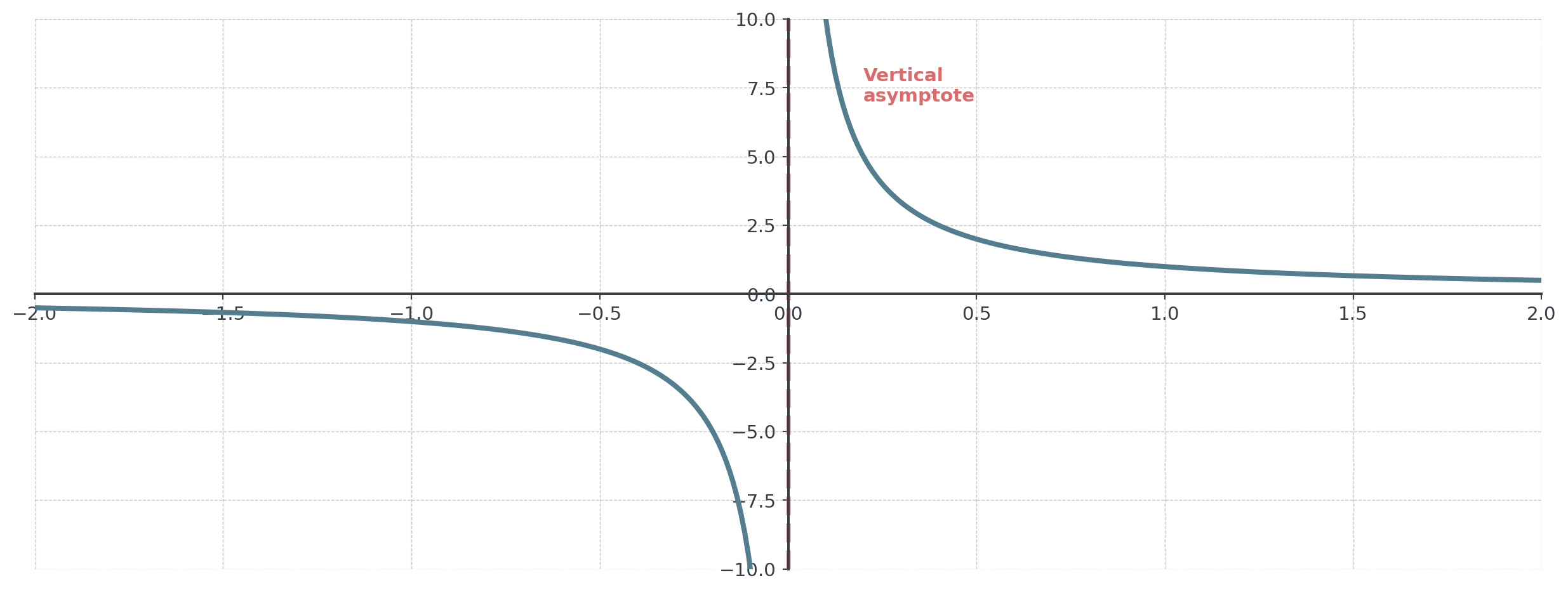
\(\lim_{x \to 0^-} f(x) = -\infty\) and \(\lim_{x \to 0^+} f(x) = +\infty\)

Quick Practice - 10 Minutes

Individual Exercise

Work individually, then compare

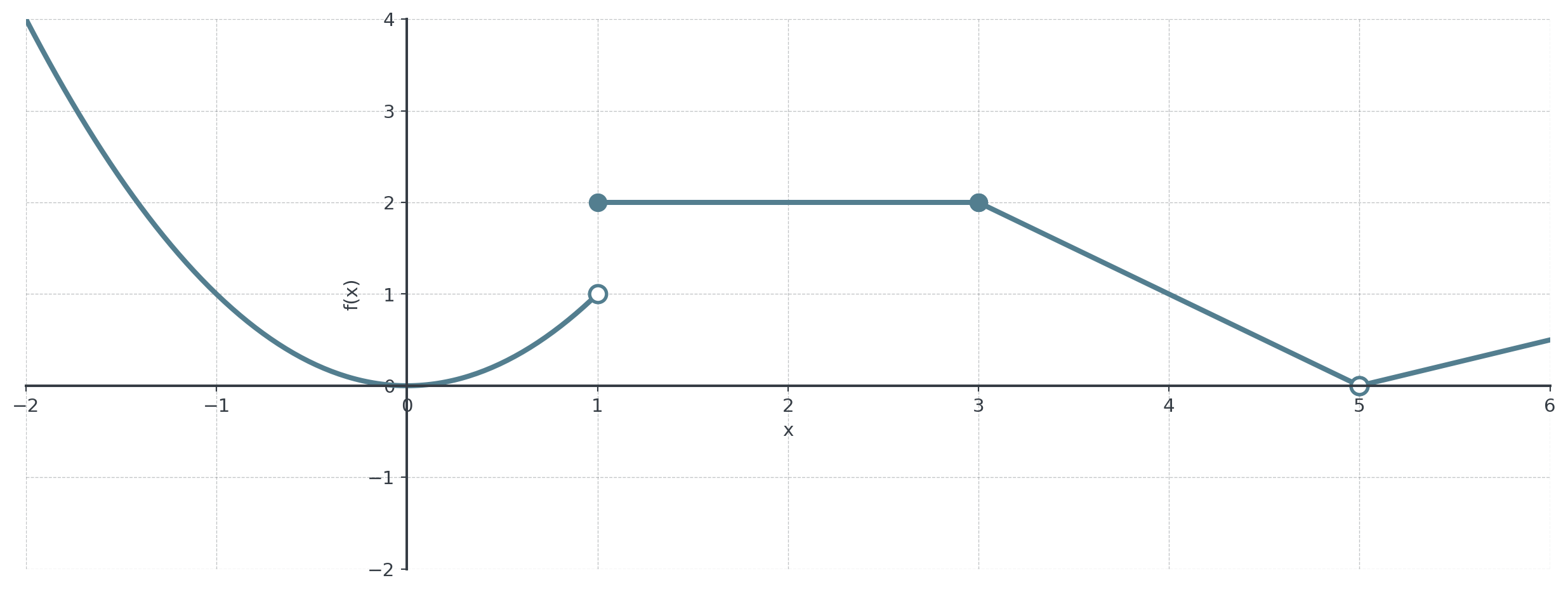
Your Tasks

Find the following:

\(\lim_{x \to 1^-} f(x)\) and \(\lim_{x \to 1^+} f(x)\)
\(\lim_{x \to 3} f(x)\)
\(\lim_{x \to 5^-} f(x)\) and \(\lim_{x \to 5^+} f(x)\)

. . .

Trace the curve from each direction. The y-value you approach is the limit.

Break - 10 Minutes

Part D: Continuity at a Point

The Three Conditions for Continuity

A function \(f\) is continuous at \(x = a\) if:

\(f(a)\) is defined (the function has a value at \(a\))
\(\lim_{x \to a} f(x)\) exists (the limit exists)
\(\lim_{x \to a} f(x) = f(a)\) (limit equals the function value)

. . .

Business Interpretation

Continuity means “no sudden jumps”, important for:

Smooth production processes
Gradual price changes
Predictable cost functions

Visual Continuity Test

Example: Production Capacity

A factory’s cost function changes at 1000 units:

\[C(x) = \begin{cases} 5x + 1000 & \text{if } x < 1000 \\ 3x + 3000 & \text{if } x \geq 1000 \end{cases}\]

. . .

Question: Any idea how this might look?

Production Capacity: Visualization

. . .

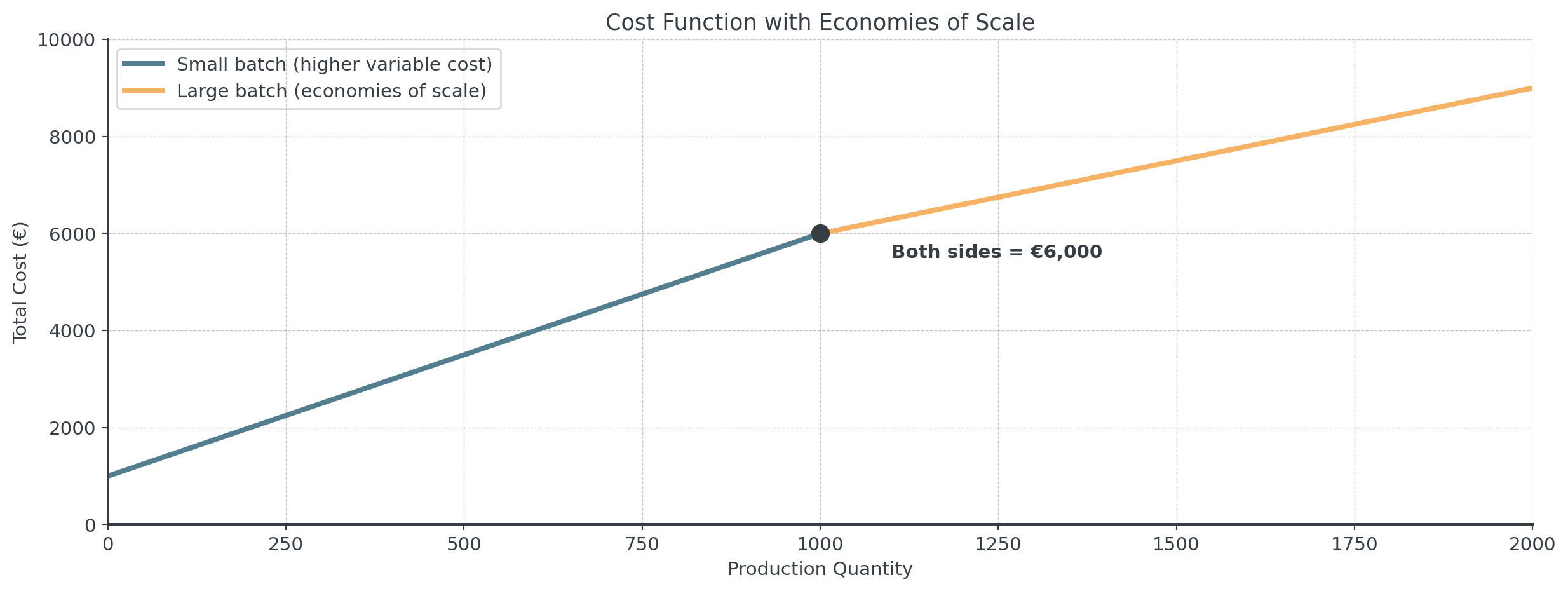
This is continuous! The company planned the transition carefully.

Guided Practice - 20 Minutes

Practice Set A: Limit Evaluation

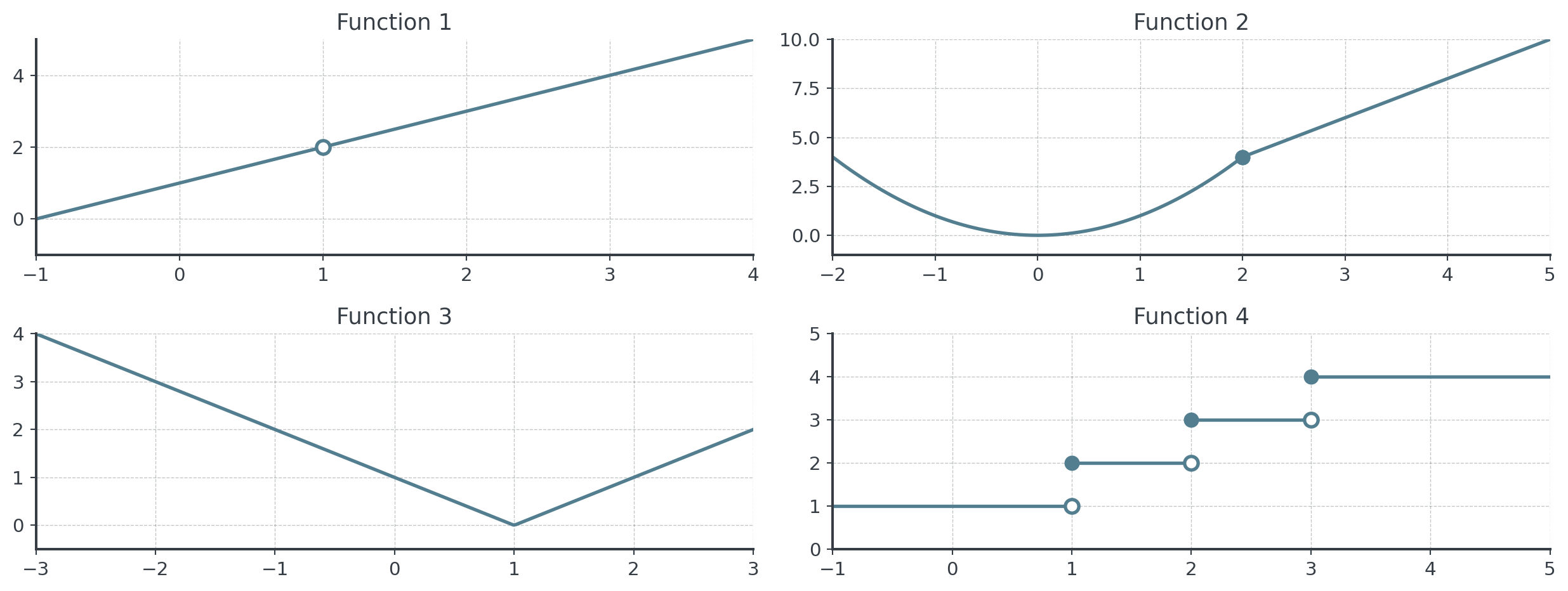
Practice Set A: Questions

Work individually for 5 minutes

Evaluate the limits from the previous graphs:

Function 1: \(\lim_{x \to 1} f(x)\)
Function 2: \(\lim_{x \to 2^-} f(x)\) and \(\lim_{x \to 2^+} f(x)\)
Function 3: \(\lim_{x \to 1} f(x)\)
Function 4: Does \(\lim_{x \to 2} f(x)\) exist?

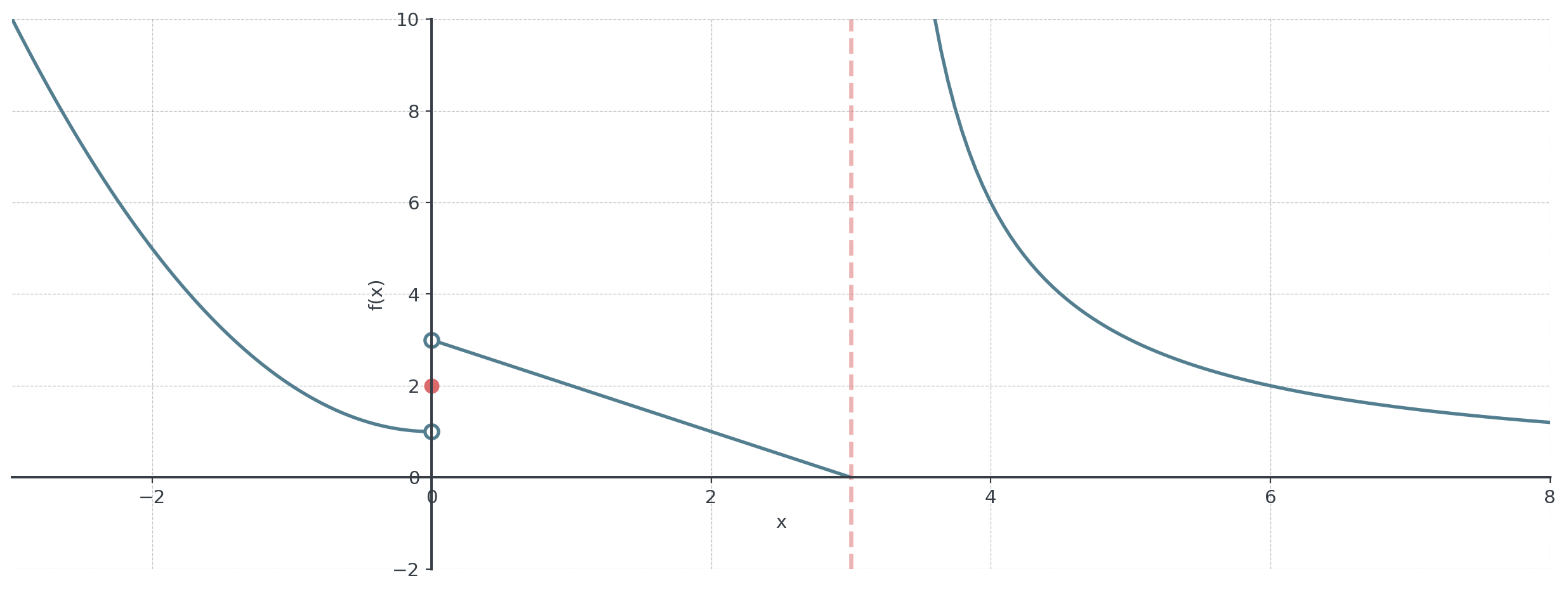
Practice Set B: Continuity Analysis

For the function below, determine where it is continuous:

\[f(x) = \begin{cases} x^2 + 1 & \text{if } x < 0 \\ 2 & \text{if } x = 0 \\ -x + 3 & \text{if } 0 < x < 3 \\ \frac{6}{x-3} & \text{if } x > 3 \end{cases}\]

Check continuity at \(x = 0\)
Check continuity at \(x = 3\)
Sketch the function
Where is \(f\) continuous?

Coffee Break - 15 Minutes

Business Applications

Shipping Cost Models

Online retailers often use step functions for shipping:

. . .

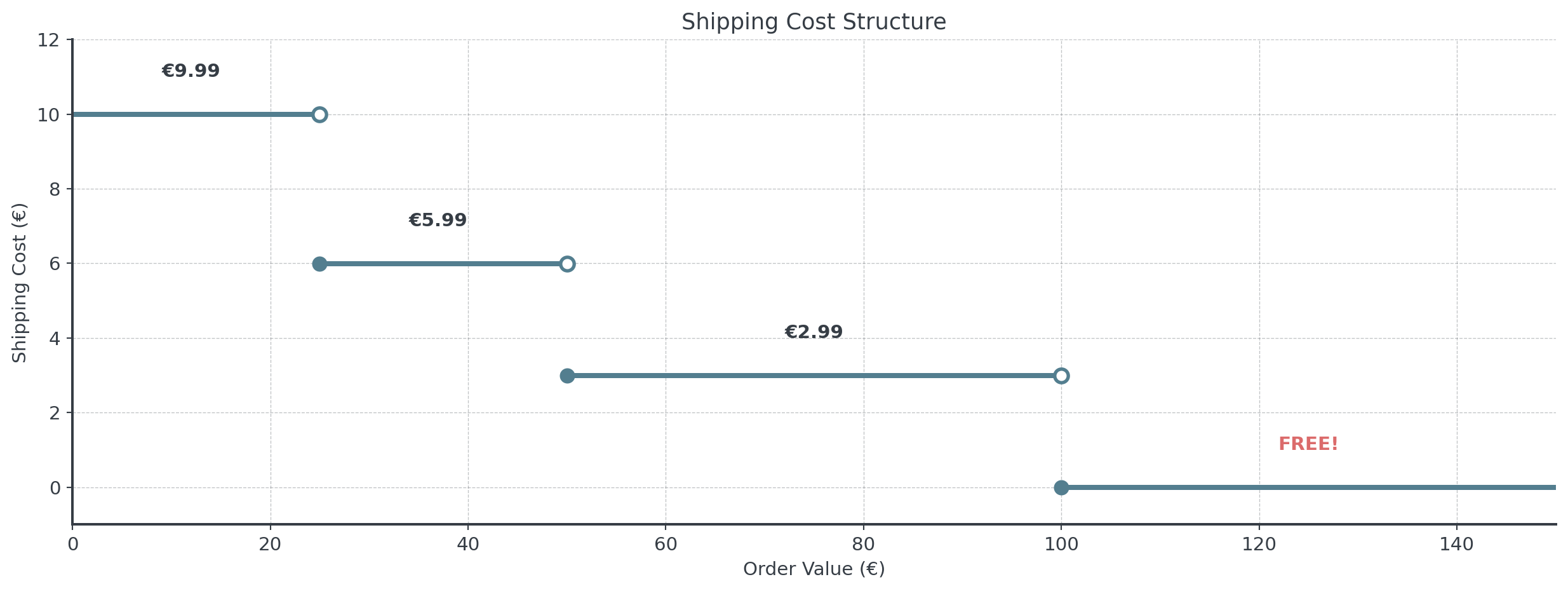
Question: How does this pricing structure influence customer behavior?

Government Price Intervention

Demand exceeds threshold, government releases emergency reserves:

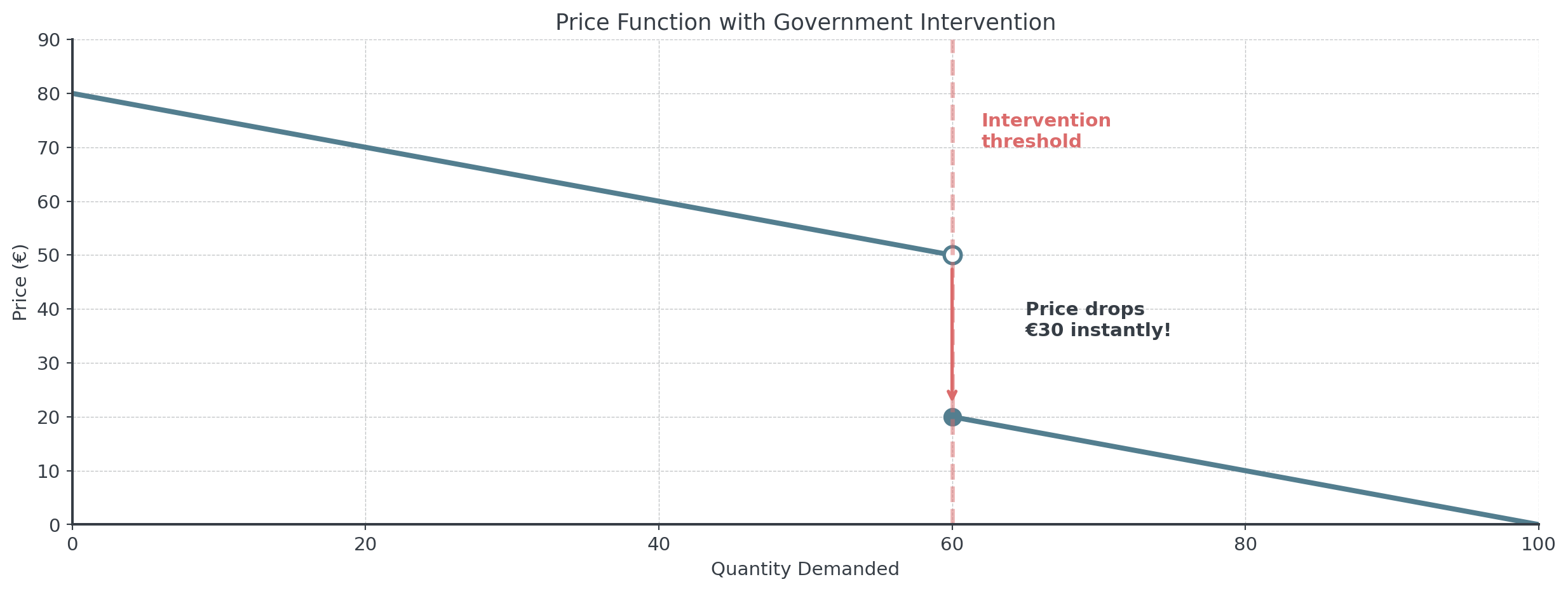
Real-World

Examples of Discontinuous Price Functions

Government reserves released when prices exceed threshold
Rent control kicking in above certain income levels
Tiered utility pricing with usage thresholds
Tariffs applied when imports exceed quotas

. . .

Policy interventions often create discontinuities. Limits help us analyze prices “just before” and “just after” the threshold.

Economic: Long-Run Average Cost

Business Context: A company’s total cost function is: \[C(x) = 5000 + 20x + 0.001x^2\]

. . .

Question: What happens to average cost in the long run?

. . .

\[\lim_{x \to \infty} \overline{C}(x) = \lim_{x \to \infty} \left(\frac{5000}{x} + 20 + 0.001x\right)\]

. . .

\(\frac{5000}{x} \to 0\) (fixed costs spread over many units)
\(20 \to 20\) (constant variable cost)
\(0.001x \to \infty\) (diseconomies of scale eventually dominate)

Part E: Additional Limit Practice

Mastering Limit Evaluation

Evaluating limits requires recognizing the type of limit!

. . .

Direct substitution first - if the function is continuous, just plug in!
Form 0/0 - factor and simplify
Form ∞/∞ - compare degrees (rational functions)
One-sided limits differ - limit doesn’t exist
Infinite limits - vertical asymptote behavior

. . .

Forms like \(\frac{0}{0}\) or \(\frac{\infty}{\infty}\) are indeterminate - the form alone doesn’t tell you the answer. The limit could be any number! You must apply techniques (factoring, simplifying) to find the actual value.

Practice Set A: Algebraic Limits

Work individually for 8 minutes

Evaluate these limits:

\(\displaystyle\lim_{x \to 3} \frac{x^2 - 9}{x^2 - 5x + 6}\)
\(\displaystyle\lim_{x \to 0} \frac{x^3 - x}{x}\)
\(\displaystyle\lim_{x \to 4} \frac{\sqrt{x} - 2}{x - 4}\)

Practice Set B: Limits at Infinity

Work individually for 5 minutes

Evaluate these limits:

\(\displaystyle\lim_{x \to \infty} \frac{3x^2 + 2x}{5x^2 - 1}\)
\(\displaystyle\lim_{x \to \infty} \frac{x + 1}{x^3 - 2}\)
\(\displaystyle\lim_{x \to -\infty} \frac{2x^3}{x^2 + 1}\)
\(\displaystyle\lim_{x \to \infty} \frac{4x^2 - 3x + 1}{2x^2 + x}\)

Practice Set C: One-Sided and Infinite

Work individually for 5 minutes

\(\displaystyle\lim_{x \to 0^+} \frac{1}{x}\)
\(\displaystyle\lim_{x \to 0^-} \frac{1}{x}\)
Does \(\displaystyle\lim_{x \to 0} \frac{1}{x}\) exist? Why or why not?
\(\displaystyle\lim_{x \to 2^-} \frac{x}{x - 2}\) and \(\displaystyle\lim_{x \to 2^+} \frac{x}{x - 2}\)

Collaborative Problem-Solving - 30 Minutes

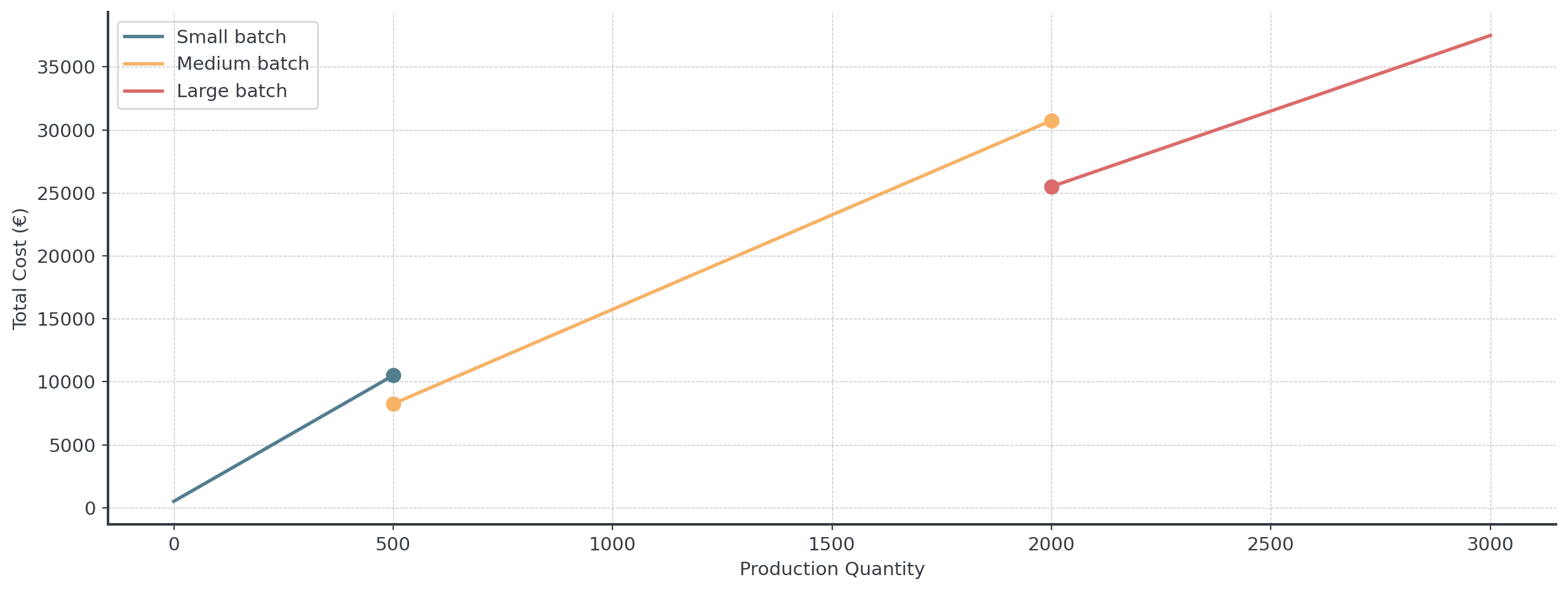
Group Challenge: Production Planning

A manufacturing company has this cost structure:

Small batches (< 500 units): \(C_1(x) = 20x + 500\)
Medium batches (500-2000 units): \(C_2(x) = 15x + 750\)
Large batches (> 2000 units): \(C_3(x) = 12x + 1500\)

Group Challenge: Tasks

Work in groups of 3-4

Write the complete piecewise cost function
Identify all points of discontinuity
Calculate limits at each transition point
Determine which transitions are continuous
Graph the cost function
Recommend: Should the company smooth these transitions?

Wrap-Up & Key Takeaways

Today’s Essential Concepts

Limits describe approaching behavior - what happens as we get close
One-sided limits help analyze jumps and breaks
Continuity requires three conditions - defined, limit exists, they match
Discontinuity types: removable (holes), jump, infinite (asymptotes)
Business functions often have discontinuities - and that’s okay!
Graphical analysis is powerful for understanding limits

. . .

Limits are the foundation of calculus. Next session, we’ll use them to define derivatives!

Final Assessment - 5 Minutes

Quick Check

Work individually, then we compare

For \(f(x) = \frac{x^2 - 9}{x - 3}\): Find \(\lim_{x \to 3} f(x)\) and is \(f\) continuous at \(x = 3\)?
A parking fee function: \[P(t) = \begin{cases} 5 & \text{if } 0 < t \leq 2 \\ 10 & \text{if } 2 < t \leq 4 \\ 20 & \text{if } t > 4 \end{cases}\] Where is \(P(t)\) discontinuous?

Next Session Preview

Coming Up: The Derivative

From average rate of change to instantaneous rate
The derivative as a limit
Marginal cost, revenue, and profit
Finding tangent lines to curves

. . .

Complete Tasks 05-01

Focus on graphical limit evaluation
Practice identifying discontinuity types
Master the limit evaluation strategies we covered today

. . .

See you next time for derivatives!

Appendix I: Practice Set B

Appendix II: Group Challenge