Calculator Training - Casio FX-991DE X

Mastering Your Calculator for Sections 1-5

Introduction

Welcome to Calculator Training!

Your Casio FX-991DE X is a powerful tool

• Today we’ll learn how to use it efficiently for the topics in Sections 1-5
• The calculator can verify your manual work and speed up calculations

. . .

This session is organized into 5 parts matching the course sections you’ve completed.

. . .

Important: Exams often require you to show your work, so use the calculator to check, not replace understanding

Session Structure

Part	Section	Topics
1	Mathematical Foundations	Fractions, powers, roots, logarithms
2	Equations	Polynomial solver, systems of equations
3	Functions	f(x)/g(x), value tables
4	Advanced Functions	Exponential, trigonometric
5	Differential Calculus	Derivatives

Getting to Know Your Calculator

The MENU Screen

MENU screen showing available applications

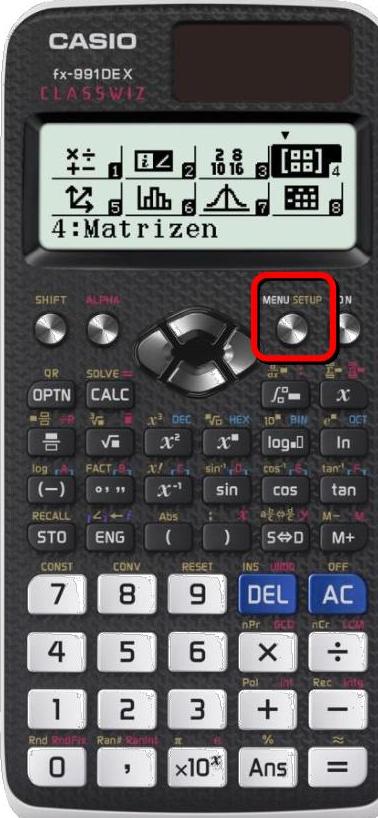
• Press MENU to see all applications
• Use arrow keys to navigate the icon grid, press number or = to select
• 1: Berechnungen (Calculate) is your main mode

Essential Settings

Before we begin, let’s configure the calculator:

1. Press SHIFT MENU (Setup)
2. Select 1: Eingabe/Ausgabe → 1: Math –> Math for natural display
3. Select 2: Winkeleinheit → 1: Gradmaß (D) for degrees

Settings menu

. . .

The natural display mode shows fractions and roots as you write them on paper!

Menu Navigation

Keyboard layout with key functions

• Use SHIFT + template keys for calculus (d/dx, Σ, Π)
• Press MENU then navigate with arrow keys or press A for Gleichung/Funkt
• CALC button for evaluating expressions with variables

Part 1: Mathematical Foundations

Connecting to Section 01

In Section 01, you learned:

• Number systems and set theory
• Order of operations and exponents
• Advanced factorization and radicals
• Logarithms and algebraic substitution

. . .

Now let’s see how your calculator handles these!

Entering Fractions

Two ways to enter fractions:

Mixed fraction: \(3\frac{1}{2}\)

• Press SHIFT + fraction key (for mixed fraction template)
• Enter: 3 → 1 → 2

Improper fraction: \(\frac{7}{2}\)

• Press fraction key
• Enter: 7 → 2

. . .

Use the arrow keys to move between numerator and denominator fields.

Fraction Calculations

Example: Calculate \(\frac{2}{3} + 1\frac{1}{2}\)

. . .

Fraction calculation example

. . .

Result: \(\frac{13}{6}\)

. . .

To convert between improper and mixed fractions:

. . .

• Press S <-> D for conversion

. . .

So far, nothing is really new, right?

Calculation History

A time-saving feature:

• Press ↑ (up arrow) to recall your previous calculation
• Edit the expression and press = to recalculate
• Navigate through multiple previous calculations with ↑ and ↓

. . .

This is very useful when you made a small mistake or want to try different values!

. . .

This only works as long as you don’t click the ON button, change the computation mode, or reset the data!

Percentage Calculations

Using the percent function:

Press SHIFT then ANS to access percentage calculations.

. . .

Example: What is 15% of 240?

. . .

Enter: 240 × 15 SHIFT ANS =

. . .

Result: 36

. . .

Example: Increase 200 by 8%

. . .

Enter: 200 + 200 × 8 SHIFT ANS =

. . .

Result: 216

. . .

You can always just use 0.08 for 8% as well!

Powers and Roots

Powers and roots can also be easily computed using a calculator:

. . .

Example 1: Calculate \(5^3 + \sqrt[4]{16}\)

. . .

Enter: 5 ^ 3 + SHIFT x^ 4 → 16 =

. . .

Result: 127

. . .

Example 2: Calculate \((2^3 + \sqrt[3]{27}) \times \sqrt[5]{32}\)

. . .

Enter: ( 2 ^ 3 + SHIFT x^ 3 → 27 ) × SHIFT x^ 5 → 32 =

. . .

Result: 128

Scientific Notation

For very large or small numbers:

Use the ×10ˣ button to enter scientific notation.

. . .

Example 1: Enter \(6.022 \times 10^{23}\)

. . .

Enter: 6.022 10ˣ 23 =

. . .

Example 2: Calculate \(\frac{1.5 \times 10^8}{3 \times 10^4}\)

. . .

Enter: 1.5 10ˣ 8 ÷ 3 10ˣ 4 =

. . .

Result: \(5 \times 10^3 = 5000\)

Logarithms

Your calculator handles all three logarithm types:

Function	Access
\(\log_{10}(x)\)	SHIFT + (-) button
\(\ln(x)\)	ln button
\(\log_a(b)\)	log (log button)

. . .

Example: Calculate \(\log_2(32)\)

. . .

Enter: log 2 → 32 =

. . .

Result: 5 (because \(2^5 = 32\))

Memory Variables

Store values for repeated use:

• Variables available: A, B, C, D, E, F, x, y, M
• Store: Enter value, press STO, then variable letter (no shift/alpha)
• Recall: Press ALPHA + variable letter

. . .

Example: Store 3.14159 in A

• Enter 3.14159 → STO → A
• Use later: 2 × ALPHA A = gives 6.28318

. . .

Ans automatically stores your last result!

The Ans Button

Using your last result efficiently:

The Ans button recalls your last calculation result.

• Ans is automatically inserted when you start with an operator

. . .

Example: Calculate \(5 + 3\), then multiply by 2:

. . .

• Enter: 5 + 3 = → Result: 8
• Enter: × 2 = → Calculator shows Ans × 2 = 16

. . .

Chain calculations become much faster with Ans!

The CALC Button

Evaluate expressions with different values:

The CALC button lets you enter an expression with variables.

1. Enter an expression with variables (e.g., 3A + B)
2. Press CALC
3. Enter values when prompted (A = ?, B = ?)
4. Press = to see the result

. . .

Example: Evaluate \(3A + B\) for \(A = 5\), \(B = 10\)

. . .

• Enter: 3 ALPHA A + ALPHA B → CALC → 5 = 10 =
• Result: 25

Prime Factorization (FACT)

Factor integers into prime factors:

1. Enter a positive integer and press =
2. Press SHIFT + FACT

. . .

Example: Find the prime factorization of 84

. . .

• Enter: 84 = then SHIFT + FACT
• Result: \(2^2 \times 3 \times 7\)

. . .

Works for integers up to 10 digits. Useful for simplifying fractions!

GCD and LCM

Greatest Common Divisor and Least Common Multiple:

Access GCD and LCM functions via ALPHA + * or ALPHA + /.

Function	Syntax	Example
GCD	GCD(a; b)	GCD(24; 36) = 12
LCM	LCM(a; b)	LCM(24; 36) = 72

. . .

Example: Find GCD(48, 180)

. . .

• Enter: ALPHA + * then GCD(48; 180) =
• Result: 12

. . .

Useful for simplifying fractions: \(\frac{48}{180} = \frac{48 \div 12}{180 \div 12} = \frac{4}{15}\)

Practice: Part 1

Try these on your calculator:

1. Calculate: \(\frac{5}{8} + \frac{3}{4} - \frac{1}{2}\)

2. Evaluate: \(\sqrt{144} + 3^4 - 2^5\)

3. Find: \(\log(1000) + \ln(e^2)\)

4. Verify: \(\log_3(81) = 4\)

5. Find the prime factorization of 360

6. Calculate GCD(72, 120) and LCM(72, 120)

7. Use CALC to evaluate \(2x^2 + 3x - 5\) for \(x = 4\)

Part 2: Equations & Problem-Solving

Connecting to Section 02

In Section 02, you learned to solve:

• Linear equations and word problems
• Systems of linear equations
• Quadratic and biquadratic equations
• Fractional, radical, and cubic equations

. . .

The calculator has powerful equation-solving modes!

Accessing the Equation Solver

From MENU:

1. Press MENU → A (Gleichung/Funkt)
2. Choose your equation type:
   • 1: Gleichungssyst. = Systems of linear equations
   • 2: Polynom-Gleich. = Polynomial equations

Solving Quadratic Equations

Solve \(x^2 + 2x - 2 = 0\)

1. Press MENU → A → 2 (Polynom-Gleich.)
2. Select Grad: 2
3. Enter coefficients: a = 1, b = 2, c = -2
4. Press = to see solutions

SOLVE function in action

Interpreting Polynomial Solutions

The calculator shows:

• \(x_1 = -1 + \sqrt{3}\)
• \(x_2 = -1 - \sqrt{3}\)

Press = repeatedly to cycle through all solutions.

. . .

After the two x-values, it also shows you the vertex!

Solving Systems of Equations

Solve the system:

\[\begin{cases} x - y + z = 2 \\ x + y - z = 0 \\ -x + y + z = 4 \end{cases}\]

1. Press MENU → A → 1 → 3 Unbekannte

2. Enter coefficients in matrix form!

3. Press = for solution: \(x=1, y=1, z=2\)

2×2 Systems: Market Equilibrium

From Section 02: Find equilibrium where supply equals demand

\[\begin{aligned} Q_d &= 100 - 2P \quad \text{(Demand)} \\ Q_s &= 20 + 3P \quad \text{(Supply)} \end{aligned}\]

. . .

Rewrite as system: \[\begin{cases} Q + 2P = 100 \\ Q - 3P = 20 \end{cases}\]

. . .

Calculator solution: \(P = 16\), \(Q = 68\)

The SOLVE Function I

Newton’s method for solving any equation:

SOLVE (accessed via SHIFT + CALC) uses Newton’s approximation method to find solutions.

. . .

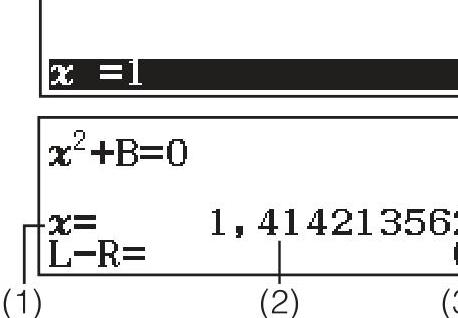
1. Enter an equation (e.g., x² + B = 0)
2. Press SHIFT + CALC (SOLVE)
3. Enter an initial guess for x and values for other variables
4. Press = to find the solution

The SOLVE Function II

Newton’s method for solving any equation:

Example: Solve \(x^2 - 2 = 0\) (find \(\sqrt{2}\))

• Enter: ALPHA x² - 2 → SHIFT CALC → initial guess: 1 =
• Result: \(x = 1.414213562\) (which is \(\sqrt{2}\))

. . .

SOLVE uses numerical methods, so:

• Results depend on your initial guess
• Multiple solutions require different starting points
• The closer your guess, the faster and more reliable the result

Practice: Part 2

Try these equation problems:

1. Solve: \(x^2 - 5x + 6 = 0\)

2. Solve: \(2x^2 + 3x - 5 = 0\)

3. Solve the system: \[\begin{cases} 3x + 2y = 18 \\ x - y = 1 \end{cases}\]

4. Find break-even: \(P(x) = -x^2 + 10x - 16 = 0\)

5. Use SOLVE to find where \(x^3 - 5x + 3 = 0\) (start with \(x = 1\))

Break - 10 Minutes

Part 3: Functions as Business Models

Connecting to Section 03

In Section 03, you learned:

• Function concepts and notation \(f(x)\)
• Linear functions and break-even analysis
• Quadratic functions and optimization
• Function transformations

. . .

Your calculator can store and evaluate function definitions!

Defining f(x) and g(x)

Register a function for repeated use:

1. Press MENU → 9 (Tabellen)
2. Enter your function expression for \(f(x)\)
3. You can also define a second function \(g(x)\)
4. Press = to continue to table settings

. . .

Once defined in Tabellen mode, the function is stored for evaluation.

Evaluating Functions

Once f(x) is defined in Tabellen mode:

The calculator generates a table showing function values:

• Set Start, Ende, and Inkre to define x-values
• The table displays both x and f(x) values

. . .

Example: \(f(x) = x^2 - 4x + 3\)

• Try to compute f(x) from x=0 to x=3 with step 1
• What can you see?

. . .

This helps verify zeros and critical points!

Composite Functions

Evaluating composite functions step-by-step:

. . .

For \(f(g(x))\), work from inside out:

1. First calculate \(g(x)\) at your value
2. Then use that result in \(f(x)\)

. . .

Example: \(f(x) = 2x + 1\), \(g(x) = x^2\)

. . .

• To find \(f(g(3))\):
• \(g(3) = 3^2 = 9\)
• \(f(9) = 2(9) + 1 = 19\)

Practice: Part 3

Try these function exercises:

1. Define \(f(x) = 3x^2 - 12x + 9\) and find \(f(0)\), \(f(1)\), \(f(2)\), \(f(3)\)

2. For \(f(x) = x + 2\) and \(g(x) = x^2\), calculate \(f(g(2))\) and \(g(f(2))\)

3. Create a table for \(f(x) = -x^2 + 4x\) from \(x = 0\) to \(x = 4\)

Part 4: Advanced Functions

Connecting to Section 04

In Section 04, you learned:

• Polynomial and power functions
• Exponential functions and growth/decay
• Trigonometric functions
• Rational and logarithmic functions

. . .

This section is shorter, as many concepts require understanding, not just calculation.

Exponential Calculations

Key buttons for exponential functions:

Operation	Keys
\(e^x\)	SHIFT + ln
\(10^x\)	SHIFT + log
\(x^n\)	Use x^ key

. . .

Examples:

• \(e^2 = 7.389...\)
• \(10^{1.5} = 31.62...\)
• \(2^{10} = 1024\)

Trigonometric Functions

Make sure angle mode is set correctly!

Check indicator: D = Degrees, R = Radians

Function	Keys
\(\sin(x)\)	sin
\(\cos(x)\)	cos
\(\tan(x)\)	tan
\(\sin^{-1}(x)\)	SHIFT + sin

. . .

Example: \(\sin(30°) = 0.5\)

Practice: Part 4

Try these calculations:

1. Calculate: \(e^3\) and \(e^{-1}\)

2. Find: \(\sin(45°)\), \(\cos(60°)\), \(\tan(30°)\)

3. What angle has \(\sin(\theta) = 0.5\)?

4. Convert \(45°\) to radians

Coffee Break - 15 Minutes

Part 5: Differential Calculus

Connecting to Section 05

In Section 05, you learned:

• Limits and continuity
• The derivative as rate of change
• Differentiation rules
• Optimization and curve sketching

. . .

This is the most important calculator section, numerical derivatives!

Accessing Calculus Functions

Access via template keys:

In Math mode, calculus templates are available via SHIFT + specific keys:

Function	Access
Derivative	SHIFT + ∫ (d/dx template)
Summation	SHIFT + x (Σ template)
Product	ALPHA + x (Π template)

. . .

This can sometimes be really helpful!

Numerical Derivatives

Syntax: \(\frac{d}{dx}(f(x))\Big|_{x=a}\)

The calculator computes the derivative at a specific point.

. . .

Example: Find \(f'(\frac{\pi}{2})\) for \(f(x) = \sin(x)\)

• Enter: SHIFT + ∫ (d/dx) → enter sin(x) → set x = π/2 → press =
• Result: 0 (as expected, since \(\cos(\frac{\pi}{2}) = 0\))

. . .

Let’s try this together with the proper function.

Using Derivatives: Step by Step

To find \(f'(2)\) for \(f(x) = x^3 - 3x^2 + 2\):

. . .

1. Press SHIFT + ∫ to access the d/dx template
2. The template appears: \(\frac{d}{dx}(\Box)\Big|_{x=\Box}\)
3. Enter the function: x^3 - 3x^2 + 2
4. Move cursor to x-value field, enter 2
5. Press =

. . .

Result: \(f'(2) = 0\)

. . .

This confirms \(x = 2\) is a critical point!

Verifying Critical Points

Use derivatives to check if \(f'(c) = 0\):

Example: For \(f(x) = x^3 - 6x^2 + 9x\)

. . .

Point	\(f'(x)\) value	Interpretation
\(x = 1\)	0	Critical point!
\(x = 2\)	-3	Decreasing
\(x = 3\)	0	Critical point!

. . .

\(f'(c) = 0\) means critical point, but check second derivative or sign changes for max/min!

. . .

It cannot determine the derivative function for you. It only computes specific values!

Practice: Part 5

Essential derivative exercises:

1. For \(f(x) = x^2 - 4x + 3\), find \(f'(0)\), \(f'(2)\), \(f'(4)\)

2. Verify that \(x = 2\) is a critical point of \(f(x) = x^2 - 4x + 5\)

3. For \(f(x) = x^3 - 3x\), find where \(f'(x) = 0\)

4. For \(R(t) = 100t - 2t^2\) (revenue over time), find:

   • Rate of change at \(t = 10\)
   • When is revenue maximized?

5. \(C(x) = 500 + 20x + 0.1x^2\) is a cost function, find marginal cost at \(x = 50\)

Wrap-up

Quick Reference

Problem Type	Calculator Mode/Function
Quadratic/cubic equations	MENU → A → 2 (Polynom-Gleich.)
Systems of equations	MENU → A → 1 (Gleichungssyst.)
Numerical equation solving	SHIFT + CALC (SOLVE)
Evaluate with variables	CALC button
Value tables	MENU → 9 (Tabellen)
Derivatives at a point	SHIFT + ∫ (d/dx template)
Prime factorization	SHIFT + FORMAT → Primfakt.
GCD/LCM	Function menu (GCD, LCM)

Common Mistakes to Avoid

Try to avoid the following if possible.

1. Wrong angle mode - Check D/R indicator before trig calculations
2. Forgetting parentheses - Use them liberally: \(\sin(30)\) not \(\sin 30\)
3. Not closing brackets - Natural display helps avoid this
4. Division issues - Use parentheses: \((a+b)/(c+d)\)
5. Relying only on calculator - Understand why the answer is correct

Calculator vs. When to Show Work

Calculator is useful for:

• Verifying your manual calculations
• Complex arithmetic
• Solving equations to check your work

. . .

Exams typically require you to show:

• Differentiation steps (product rule, chain rule, etc.)
• Setting up equations from word problems
• Algebraic manipulation
• Interpretation of results

Final Integrated Exercise

Combine everything you’ve learned today:

A company’s profit function is \(P(x) = -0.5x^2 + 30x - 200\)

Using your calculator:

1. Find the break-even points (where \(P(x) = 0\))

2. Find the production level that maximizes profit (where \(P'(x) = 0\))

3. Calculate the maximum profit \(P(x_{max})\)

. . .

Complete the Calculator Training Tasks 01 worksheet to reinforce these skills!

Thank You!