Calculator Training - Casio FX-991DE X

Mastering Your Calculator for Sections 1-5

Dr. Nikolai Heinrichs & Dr. Tobias Vlćek

Introduction

Welcome to Calculator Training!

Your Casio FX-991DE X is a powerful tool

  • Today we’ll learn how to use it efficiently for the topics in Sections 1-5
  • The calculator can verify your manual work and speed up calculations

This session is organized into 5 parts matching the course sections you’ve completed.

Important: Exams often require you to show your work, so use the calculator to check, not replace understanding

Session Structure

Part Section Topics
1 Mathematical Foundations Fractions, powers, roots, logarithms
2 Equations Polynomial solver, systems of equations
3 Functions f(x)/g(x), value tables
4 Advanced Functions Exponential, trigonometric
5 Differential Calculus Derivatives

Getting to Know Your Calculator

The MENU Screen

MENU screen showing available applications

  • Press MENU to see all applications
  • Use arrow keys to navigate the icon grid, press number or = to select
  • 1: Berechnungen (Calculate) is your main mode

Essential Settings

Before we begin, let’s configure the calculator:

  1. Press SHIFT MENU (Setup)
  2. Select 1: Eingabe/Ausgabe → 1: Math –> Math for natural display
  3. Select 2: Winkeleinheit → 1: Gradmaß (D) for degrees

Settings menu

The natural display mode shows fractions and roots as you write them on paper!

Part 1: Mathematical Foundations

Connecting to Section 01

In Section 01, you learned:

  • Number systems and set theory
  • Order of operations and exponents
  • Advanced factorization and radicals
  • Logarithms and algebraic substitution

Now let’s see how your calculator handles these!

Entering Fractions

Two ways to enter fractions:

Mixed fraction: \(3\frac{1}{2}\)

  • Press SHIFT + fraction key (for mixed fraction template)
  • Enter: 3 → 1 → 2

Improper fraction: \(\frac{7}{2}\)

  • Press fraction key
  • Enter: 7 → 2

Use the arrow keys to move between numerator and denominator fields.

Fraction Calculations

Example: Calculate \(\frac{2}{3} + 1\frac{1}{2}\)

Fraction calculation example

Result: \(\frac{13}{6}\)

To convert between improper and mixed fractions:

  • Press S <-> D for conversion

So far, nothing is really new, right?

Calculation History

A time-saving feature:

  • Press ↑ (up arrow) to recall your previous calculation
  • Edit the expression and press = to recalculate
  • Navigate through multiple previous calculations with ↑ and ↓

This is very useful when you made a small mistake or want to try different values!

This only works as long as you don’t click the ON button, change the computation mode, or reset the data!

Percentage Calculations

Using the percent function:

Press SHIFT then ANS to access percentage calculations.

Example: What is 15% of 240?

Enter: 240 × 15 SHIFT ANS =

Result: 36

Example: Increase 200 by 8%

Enter: 200 + 200 × 8 SHIFT ANS =

Result: 216

You can always just use 0.08 for 8% as well!

Powers and Roots

Powers and roots can also be easily computed using a calculator:

Example 1: Calculate \(5^3 + \sqrt[4]{16}\)

Enter: 5 ^ 3 + SHIFT x^ 4 → 16 =

Result: 127

Example 2: Calculate \((2^3 + \sqrt[3]{27}) \times \sqrt[5]{32}\)

Enter: ( 2 ^ 3 + SHIFT x^ 3 → 27 ) × SHIFT x^ 5 → 32 =

Result: 128

Scientific Notation

For very large or small numbers:

Use the ×10ˣ button to enter scientific notation.

Example 1: Enter \(6.022 \times 10^{23}\)

Enter: 6.022 10ˣ 23 =

Example 2: Calculate \(\frac{1.5 \times 10^8}{3 \times 10^4}\)

Enter: 1.5 10ˣ 8 ÷ 3 10ˣ 4 =

Result: \(5 \times 10^3 = 5000\)

Logarithms

Your calculator handles all three logarithm types:

Function Access
\(\log_{10}(x)\) SHIFT + (-) button
\(\ln(x)\) ln button
\(\log_a(b)\) log (log button)

Example: Calculate \(\log_2(32)\)

Enter: log 2 → 32 =

Result: 5 (because \(2^5 = 32\))

Memory Variables

Store values for repeated use:

  • Variables available: A, B, C, D, E, F, x, y, M
  • Store: Enter value, press STO, then variable letter (no shift/alpha)
  • Recall: Press ALPHA + variable letter

Example: Store 3.14159 in A

  • Enter 3.14159 → STO → A
  • Use later: 2 × ALPHA A = gives 6.28318

Ans automatically stores your last result!

The Ans Button

Using your last result efficiently:

The Ans button recalls your last calculation result.

  • Ans is automatically inserted when you start with an operator

Example: Calculate \(5 + 3\), then multiply by 2:

  • Enter: 5 + 3 = → Result: 8
  • Enter: × 2 = → Calculator shows Ans × 2 = 16

Chain calculations become much faster with Ans!

The CALC Button

Evaluate expressions with different values:

The CALC button lets you enter an expression with variables.

  1. Enter an expression with variables (e.g., 3A + B)
  2. Press CALC
  3. Enter values when prompted (A = ?, B = ?)
  4. Press = to see the result

Example: Evaluate \(3A + B\) for \(A = 5\), \(B = 10\)

  • Enter: 3 ALPHA A + ALPHA B → CALC → 5 = 10 =
  • Result: 25

Prime Factorization (FACT)

Factor integers into prime factors:

  1. Enter a positive integer and press =
  2. Press SHIFT + FACT

Example: Find the prime factorization of 84

  • Enter: 84 = then SHIFT + FACT
  • Result: \(2^2 \times 3 \times 7\)

Works for integers up to 10 digits. Useful for simplifying fractions!

GCD and LCM

Greatest Common Divisor and Least Common Multiple:

Access GCD and LCM functions via ALPHA + * or ALPHA + /.

Function Syntax Example
GCD GCD(a; b) GCD(24; 36) = 12
LCM LCM(a; b) LCM(24; 36) = 72

Example: Find GCD(48, 180)

  • Enter: ALPHA + * then GCD(48; 180) =
  • Result: 12

Useful for simplifying fractions: \(\frac{48}{180} = \frac{48 \div 12}{180 \div 12} = \frac{4}{15}\)

Practice: Part 1

Try these on your calculator:

  1. Calculate: \(\frac{5}{8} + \frac{3}{4} - \frac{1}{2}\)

  2. Evaluate: \(\sqrt{144} + 3^4 - 2^5\)

  3. Find: \(\log(1000) + \ln(e^2)\)

  4. Verify: \(\log_3(81) = 4\)

  5. Find the prime factorization of 360

  6. Calculate GCD(72, 120) and LCM(72, 120)

  7. Use CALC to evaluate \(2x^2 + 3x - 5\) for \(x = 4\)

Part 2: Equations & Problem-Solving

Connecting to Section 02

In Section 02, you learned to solve:

  • Linear equations and word problems
  • Systems of linear equations
  • Quadratic and biquadratic equations
  • Fractional, radical, and cubic equations

The calculator has powerful equation-solving modes!

Accessing the Equation Solver

From MENU:

  1. Press MENU → A (Gleichung/Funkt)
  2. Choose your equation type:
    • 1: Gleichungssyst. = Systems of linear equations
    • 2: Polynom-Gleich. = Polynomial equations

Solving Quadratic Equations

Solve \(x^2 + 2x - 2 = 0\)

  1. Press MENU → A → 2 (Polynom-Gleich.)
  2. Select Grad: 2
  3. Enter coefficients: a = 1, b = 2, c = -2
  4. Press = to see solutions

SOLVE function in action

Interpreting Polynomial Solutions

The calculator shows:

  • \(x_1 = -1 + \sqrt{3}\)
  • \(x_2 = -1 - \sqrt{3}\)

Press = repeatedly to cycle through all solutions.

After the two x-values, it also shows you the vertex!

Solving Systems of Equations

Solve the system:

\[\begin{cases} x - y + z = 2 \\ x + y - z = 0 \\ -x + y + z = 4 \end{cases}\]

  1. Press MENU → A → 1 → 3 Unbekannte

  2. Enter coefficients in matrix form!

  3. Press = for solution: \(x=1, y=1, z=2\)

2×2 Systems: Market Equilibrium

From Section 02: Find equilibrium where supply equals demand

\[\begin{aligned} Q_d &= 100 - 2P \quad \text{(Demand)} \\ Q_s &= 20 + 3P \quad \text{(Supply)} \end{aligned}\]

Rewrite as system: \[\begin{cases} Q + 2P = 100 \\ Q - 3P = 20 \end{cases}\]

Calculator solution: \(P = 16\), \(Q = 68\)

The SOLVE Function I

Newton’s method for solving any equation:

SOLVE (accessed via SHIFT + CALC) uses Newton’s approximation method to find solutions.

  1. Enter an equation (e.g., x² + B = 0)
  2. Press SHIFT + CALC (SOLVE)
  3. Enter an initial guess for x and values for other variables
  4. Press = to find the solution

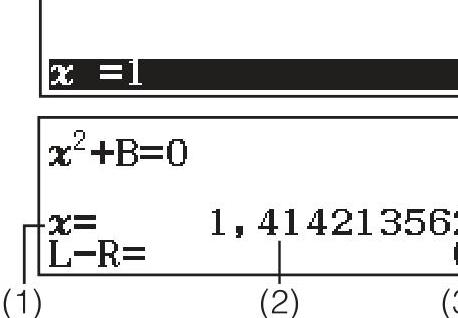
The SOLVE Function II

Newton’s method for solving any equation:

Example: Solve \(x^2 - 2 = 0\) (find \(\sqrt{2}\))

  • Enter: ALPHA x² - 2 → SHIFT CALC → initial guess: 1 =
  • Result: \(x = 1.414213562\) (which is \(\sqrt{2}\))

SOLVE uses numerical methods, so:

  • Results depend on your initial guess
  • Multiple solutions require different starting points
  • The closer your guess, the faster and more reliable the result

Practice: Part 2

Try these equation problems:

  1. Solve: \(x^2 - 5x + 6 = 0\)

  2. Solve: \(2x^2 + 3x - 5 = 0\)

  3. Solve the system: \[\begin{cases} 3x + 2y = 18 \\ x - y = 1 \end{cases}\]

  4. Find break-even: \(P(x) = -x^2 + 10x - 16 = 0\)

  5. Use SOLVE to find where \(x^3 - 5x + 3 = 0\) (start with \(x = 1\))

Break - 10 Minutes

Part 3: Functions as Business Models

Connecting to Section 03

In Section 03, you learned:

  • Function concepts and notation \(f(x)\)
  • Linear functions and break-even analysis
  • Quadratic functions and optimization
  • Function transformations

Your calculator can store and evaluate function definitions!

Defining f(x) and g(x)

Register a function for repeated use:

  1. Press MENU → 9 (Tabellen)
  2. Enter your function expression for \(f(x)\)
  3. You can also define a second function \(g(x)\)
  4. Press = to continue to table settings

Once defined in Tabellen mode, the function is stored for evaluation.

Evaluating Functions

Once f(x) is defined in Tabellen mode:

The calculator generates a table showing function values:

  • Set Start, Ende, and Inkre to define x-values
  • The table displays both x and f(x) values

Example: \(f(x) = x^2 - 4x + 3\)

  • Try to compute f(x) from x=0 to x=3 with step 1
  • What can you see?

This helps verify zeros and critical points!

Composite Functions

Evaluating composite functions step-by-step:

For \(f(g(x))\), work from inside out:

  1. First calculate \(g(x)\) at your value
  2. Then use that result in \(f(x)\)

Example: \(f(x) = 2x + 1\), \(g(x) = x^2\)

  • To find \(f(g(3))\):
  • \(g(3) = 3^2 = 9\)
  • \(f(9) = 2(9) + 1 = 19\)

Practice: Part 3

Try these function exercises:

  1. Define \(f(x) = 3x^2 - 12x + 9\) and find \(f(0)\), \(f(1)\), \(f(2)\), \(f(3)\)

  2. For \(f(x) = x + 2\) and \(g(x) = x^2\), calculate \(f(g(2))\) and \(g(f(2))\)

  3. Create a table for \(f(x) = -x^2 + 4x\) from \(x = 0\) to \(x = 4\)

Part 4: Advanced Functions

Connecting to Section 04

In Section 04, you learned:

  • Polynomial and power functions
  • Exponential functions and growth/decay
  • Trigonometric functions
  • Rational and logarithmic functions

This section is shorter, as many concepts require understanding, not just calculation.

Exponential Calculations

Key buttons for exponential functions:

Operation Keys
\(e^x\) SHIFT + ln
\(10^x\) SHIFT + log
\(x^n\) Use x^ key

Examples:

  • \(e^2 = 7.389...\)
  • \(10^{1.5} = 31.62...\)
  • \(2^{10} = 1024\)

Trigonometric Functions

Make sure angle mode is set correctly!

Check indicator: D = Degrees, R = Radians

Function Keys
\(\sin(x)\) sin
\(\cos(x)\) cos
\(\tan(x)\) tan
\(\sin^{-1}(x)\) SHIFT + sin

Example: \(\sin(30°) = 0.5\)

Practice: Part 4

Try these calculations:

  1. Calculate: \(e^3\) and \(e^{-1}\)

  2. Find: \(\sin(45°)\), \(\cos(60°)\), \(\tan(30°)\)

  3. What angle has \(\sin(\theta) = 0.5\)?

  4. Convert \(45°\) to radians

Coffee Break - 15 Minutes

Part 5: Differential Calculus

Connecting to Section 05

In Section 05, you learned:

  • Limits and continuity
  • The derivative as rate of change
  • Differentiation rules
  • Optimization and curve sketching

This is the most important calculator section, numerical derivatives!

Accessing Calculus Functions

Access via template keys:

In Math mode, calculus templates are available via SHIFT + specific keys:

Function Access
Derivative SHIFT + ∫ (d/dx template)
Summation SHIFT + x (Σ template)
Product ALPHA + x (Π template)

This can sometimes be really helpful!

Numerical Derivatives

Syntax: \(\frac{d}{dx}(f(x))\Big|_{x=a}\)

The calculator computes the derivative at a specific point.

Example: Find \(f'(\frac{\pi}{2})\) for \(f(x) = \sin(x)\)

  • Enter: SHIFT + ∫ (d/dx) → enter sin(x) → set x = π/2 → press =
  • Result: 0 (as expected, since \(\cos(\frac{\pi}{2}) = 0\))

Let’s try this together with the proper function.

Using Derivatives: Step by Step

To find \(f'(2)\) for \(f(x) = x^3 - 3x^2 + 2\):

  1. Press SHIFT + ∫ to access the d/dx template
  2. The template appears: \(\frac{d}{dx}(\Box)\Big|_{x=\Box}\)
  3. Enter the function: x^3 - 3x^2 + 2
  4. Move cursor to x-value field, enter 2
  5. Press =

Result: \(f'(2) = 0\)

This confirms \(x = 2\) is a critical point!

Verifying Critical Points

Use derivatives to check if \(f'(c) = 0\):

Example: For \(f(x) = x^3 - 6x^2 + 9x\)

Point \(f'(x)\) value Interpretation
\(x = 1\) 0 Critical point!
\(x = 2\) -3 Decreasing
\(x = 3\) 0 Critical point!

\(f'(c) = 0\) means critical point, but check second derivative or sign changes for max/min!

It cannot determine the derivative function for you. It only computes specific values!

Practice: Part 5

Essential derivative exercises:

  1. For \(f(x) = x^2 - 4x + 3\), find \(f'(0)\), \(f'(2)\), \(f'(4)\)

  2. Verify that \(x = 2\) is a critical point of \(f(x) = x^2 - 4x + 5\)

  3. For \(f(x) = x^3 - 3x\), find where \(f'(x) = 0\)

  4. For \(R(t) = 100t - 2t^2\) (revenue over time), find:

    • Rate of change at \(t = 10\)
    • When is revenue maximized?

  5. \(C(x) = 500 + 20x + 0.1x^2\) is a cost function, find marginal cost at \(x = 50\)

Wrap-up

Quick Reference

Problem Type Calculator Mode/Function
Quadratic/cubic equations MENU → A → 2 (Polynom-Gleich.)
Systems of equations MENU → A → 1 (Gleichungssyst.)
Numerical equation solving SHIFT + CALC (SOLVE)
Evaluate with variables CALC button
Value tables MENU → 9 (Tabellen)
Derivatives at a point SHIFT + ∫ (d/dx template)
Prime factorization SHIFT + FORMAT → Primfakt.
GCD/LCM Function menu (GCD, LCM)

Common Mistakes to Avoid

Try to avoid the following if possible.

  1. Wrong angle mode - Check D/R indicator before trig calculations
  2. Forgetting parentheses - Use them liberally: \(\sin(30)\) not \(\sin 30\)
  3. Not closing brackets - Natural display helps avoid this
  4. Division issues - Use parentheses: \((a+b)/(c+d)\)
  5. Relying only on calculator - Understand why the answer is correct

Calculator vs. When to Show Work

Calculator is useful for:

  • Verifying your manual calculations
  • Complex arithmetic
  • Solving equations to check your work

Exams typically require you to show:

  • Differentiation steps (product rule, chain rule, etc.)
  • Setting up equations from word problems
  • Algebraic manipulation
  • Interpretation of results

Final Integrated Exercise

Combine everything you’ve learned today:

A company’s profit function is \(P(x) = -0.5x^2 + 30x - 200\)

Using your calculator:

  1. Find the break-even points (where \(P(x) = 0\))

  2. Find the production level that maximizes profit (where \(P'(x) = 0\))

  3. Calculate the maximum profit \(P(x_{max})\)

Complete the Calculator Training Tasks 01 worksheet to reinforce these skills!

Thank You!