Section 05: Differential Calculus
Test your understanding of differentiation rules
Find the derivative of \(f(x) = (x^2 + 1)(3x - 2)\).
Differentiate \(g(x) = \frac{x^2}{x + 1}\) using the quotient rule.
For \(h(x) = 5x^{10} - 3x^2 + 7\), find \(h'(x)\).
What is the tangent line to \(f(x) = x^2\) at \(x = 3\)?
What questions do you have regarding the tasks?
Key Insight
The chain rule unlocks differentiation of composite functions, one of the most powerful and widely used techniques in calculus!
The Problem: How do we differentiate \((x^2 + 3x + 1)^{100}\)?
The Structure:
Derivative of outer (evaluated at inner) times derivative of inner:
\[\frac{d}{dx}[f(g(x))] = f'(g(x)) \cdot g'(x)\]
Or in Leibniz notation, if \(y = f(u)\) and \(u = g(x)\):
\[\frac{dy}{dx} = \frac{dy}{du} \cdot \frac{du}{dx}\]
Most Common Mistake: Forgetting to multiply by the derivative of the inner function!
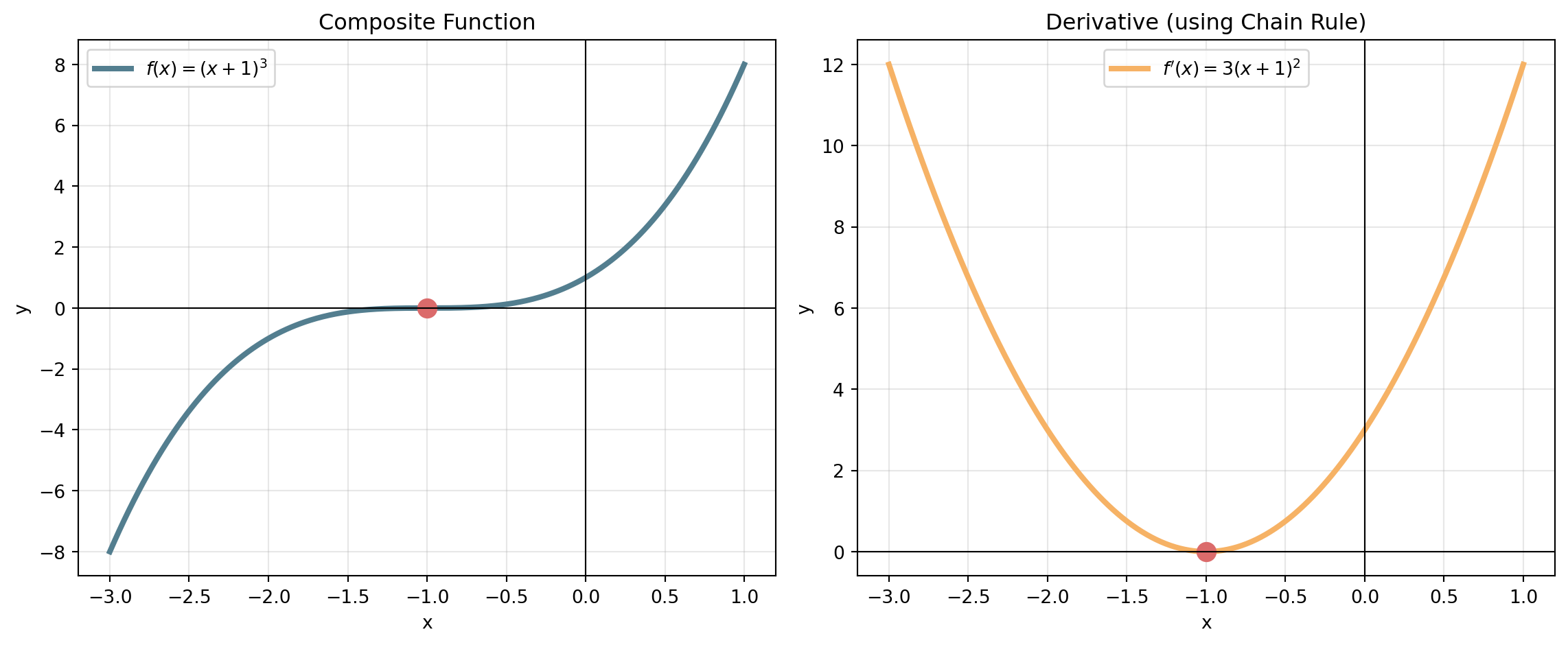
Example: Differentiate \(f(x) = (x^2 + 3x + 1)^{100}\)
Step 1: Identify inner and outer
Step 2: Apply chain rule \[f'(x) = 100(x^2 + 3x + 1)^{99} \cdot (2x + 3)\]
Notice: We never had to expand the original function!

Example: Differentiate \(g(x) = \sqrt{3x^2 + 5}\)
Rewrite: \(g(x) = (3x^2 + 5)^{1/2}\)
Example: Differentiate \(h(x) = \frac{1}{(2x - 1)^3}\)
Rewrite: \(h(x) = (2x - 1)^{-3}\)
Strategy: When you have a product with composite functions:
Example: Differentiate \(f(x) = x^2(3x + 1)^5\)
Product rule:
Factor:
Example: Differentiate \(h(x) = \sqrt{(2x + 1)^3}\)
Simplify first!
\[h(x) = (2x + 1)^{3/2}\]
\[h'(x) = \frac{3}{2}(2x + 1)^{1/2} \cdot 2\]
\[h'(x) = 3\sqrt{2x + 1}\]
Work individually for 10 minutes
Differentiate using the chain rule:
\(f(x) = (5x + 2)^4\)
\(g(x) = \sqrt{x^2 - 1}\)
\(h(x) = (x^2 + 1)^3(2x - 1)^2\)
\(k(x) = \frac{x}{(3x + 1)^2}\)
Problem: Revenue constraint \(pq = 10000\). Find \(\frac{dq}{dp}\).
Both methods give \(\frac{dq}{dp} = -\frac{10000}{p^2}\). Method 2 is called implicit differentiation.
Because sometimes Method 1 is impossible or complex!
Factory produces constant output \(Q = 100\) with labor \(L\) and capital \(K\):
\[L^{0.6} \cdot K^{0.4} = 100\]
When we write \(L^{0.6} \cdot K^{0.4} = 100\), we’re really saying:
\[L^{0.6} \cdot [K(L)]^{0.4} = 100\]
Question: What does this mean?
Every variable is secretly a function!
\(K\) depends on \(L\), we just don’t know the explicit formula!
\[L^{0.6} \cdot K^{0.4} = 100\]
The Chain Rule applies:
\[\frac{d}{dL}[K^{0.4}] = 0.4 \cdot K^{-0.6} \cdot \frac{dK}{dL}\]
Core Principle
Whenever you differentiate a term containing \(K\), multiply by \(\frac{dK}{dL}\) because \(K\) is a function of \(L\).
Step 1: Differentiate both sides with respect to \(L\)
\[\frac{d}{dL}[L^{0.6} \cdot K^{0.4}] = \frac{d}{dL}[100]\]
Step 2: Apply product rule on left side and solve for \(\frac{dK}{dL}\)
\[0.6L^{-0.4} \cdot K^{0.4} + L^{0.6} \cdot 0.4K^{-0.6} \cdot \frac{dK}{dL} = 0\]
\[\frac{dK}{dL} = -\frac{0.6L^{-0.4} \cdot K^{0.4}}{0.4L^{0.6} \cdot K^{-0.6}} = -\frac{0.6}{0.4} \cdot \frac{K}{L} = -\frac{3K}{2L}\]
What does this mean?
\[\frac{dK}{dL} = -\frac{3K}{2L}\]
The MRTS tells managers how to substitute between inputs while maintaining the same output level, crucial for cost minimization!
A company sells a product with a constant revenue of 5000:
Practice: \(pq = 5000\). Find \(\frac{dq}{dp}\) using implicit differentiation.
Result: \(\frac{dq}{dp} = -\frac{q}{p}\)
Interpretation: At any point on the demand curve, a 1% price increase requires approximately a 1% quantity decrease to maintain revenue.
When to Use Each Method
The Concept: When two or more quantities are related by an equation and both change with time, their rates of change are also related.
General Process:
Related rates problems use implicit differentiation with respect to time!
Scenario: A company’s revenue \(R\) depends on its customer base \(C\): \[R = 50\sqrt{C}\]
The company is gaining 100 new customers per month. How fast is revenue growing when \(C = 10000\) customers?
Step 1: Given relationship \(R = 50C^{1/2}\)
Step 2: Differentiate to time \(\frac{dR}{dt} = 50 \cdot \frac{1}{2}C^{-1/2} \cdot \frac{dC}{dt} = \frac{25}{\sqrt{C}} \cdot \frac{dC}{dt}\)
Step 3: Substitute given: \(\frac{dC}{dt} = 100\) customers/month, \(C = 10000\)
\[\frac{dR}{dt} = \frac{25}{\sqrt{10000}} \cdot 100 = \frac{25}{100} \cdot 100 = 25 \text{ €/month}\]
Scenario: A company’s profit \(P\) and market share \(m\) are related by: \[P = 1000m - 20m^2\]
where \(P\) is in k € and \(m\) is market share percentage. Market share is increasing at 2% per month. How fast is profit changing when \(m = 15\)%?
Step1: Differentiate \(\frac{dP}{dt} = 1000\frac{dm}{dt} - 40m\frac{dm}{dt} = (1000 - 40m)\frac{dm}{dt}\)
Step 2: Substitute given \(\frac{dm}{dt} = 2\) %/month, \(m = 15\) %
\[\frac{dP}{dt} = (1000 - 40 \cdot 15)(2) = (1000 - 600)(2) = 800\]
Answer: Profit is increasing at €800,000 per month.
Work in pairs for 15 minutes
Differentiate the following:
\(f(x) = (x^3 - 2x + 1)^{10}\)
\(g(x) = \sqrt{5x^2 + 3x - 1}\)
\(h(x) = \frac{1}{(x^2 + 1)^3}\)
\(k(x) = x(2x - 3)^4\)
Continue working in pairs for 10 minutes
Implicit Differentiation:
A company’s marketing \(M\) and sales \(S\) satisfy \(MS = 5000\). Find \(\frac{dS}{dM}\).
Budget constraint: \(2L + 3K = 120\) where \(L\) = labor, \(K\) = capital. Find \(\frac{dK}{dL}\).
Related Rates:
Business Context: A company’s revenue depends on price \(p\), which itself depends on quantity \(x\):
Question: Find \(\frac{dR}{dx}\), rate of change of revenue with respect to quantity.
Any idea how to approach this problem?
Step 1: Express \(R\) in terms of \(p\) with \(R(p) = 200p - 2p^2\)
\[\frac{dR}{dp} = 200 - 4p\]
Step 2: Find \(\frac{dp}{dx}\) with \(p(x) = 100 - 0.5x\)
\[\frac{dp}{dx} = -0.5\]
Step 3: Apply chain rule \(\frac{dR}{dx} = \frac{dR}{dp} \cdot \frac{dp}{dx}\)
\[\frac{dR}{dx} = (200 - 4p)(-0.5)\]
Now just substitute \(p = 100 - 0.5x\) into expression for \(\frac{dR}{dx}\):
\[\frac{dR}{dx} = (200 - 4(100 - 0.5x))(-0.5)\]
\[\frac{dR}{dx} = 100 - x\]
A retail chain’s profit \(P\) (in €1000) and stores \(n\) are related by:
\[P = 200\sqrt{n} - 5n\]
The company opens 4 new stores per year.
Write the relationship between \(\frac{dP}{dt}\) and \(\frac{dn}{dt}\).
How fast is profit changing when \(n = 25\) stores?
How fast is profit changing when \(n = 100\) stores?
At how many stores does profit stop growing? What does this mean for the company?
Discussion: Why does profit growth slow as the chain expands?
Think individually, then discuss with class
Question: You’re analyzing two companies:
At \(t = 0\), both have revenue of 1000 (thousand €).
| Technique | When to Use | Key Idea |
|---|---|---|
| Chain Rule | Composite \(f(g(x))\) | Outer derivative × inner derivative |
| Chain + Product | Product with composites | Product rule first, then chain |
| Implicit Diff | Variables intertwined | Differentiate both, solve for derivative |
| Related Rates | Quantities change over time | Differentiate with respect to \(t\) |
Never forget the inner derivative! This is the main mistake in chain rule problems.
Work individually and then we compare
Differentiate \((3x^2 + 1)^4\).
Price \(p\) and quantity \(q\) satisfy \(pq = 800\). Find \(\frac{dq}{dp}\).
Profit \(P = 50\sqrt{Q}\) and production grows at 8 units/month. How fast is profit growing when \(Q = 100\)?
True or False: \(\frac{d}{dx}[f(g(x))] = f'(x) \cdot g'(x)\)
Graphical Calculus Mastery
Complete Tasks 05-04!
Session 05-04 - Chain Rule & Implicit Differentiation | Dr. Nikolai Heinrichs & Dr. Tobias Vlćek | Home