Notebook 7.1 - Routing Optimization

Management Science - Bean Counter’s Delivery Excellence

Introduction

Welcome back, CEO! Bean Counter has grown to up to 10 franchise locations across some cities, and you personally want to optimize the weekly coffee bean deliveries in all cities. Currently, delivery trucks just follow a random route. Time to optimize!

The Delivery Challenge:

  • One truck leaves from Bean Counter HQ in a city
  • Must deliver coffee beans to all 10 franchises
  • Each franchise needs their specific blend
  • Fuel costs €1.50 per km
  • Driver costs €30 per hour

Your board calculated that poor routing costs Bean Counter €2,500 monthly in excess fuel and labor. Let’s fix this!

NoteHow to Use This Tutorial

Work through each section in order. Write code where marked “YOUR CODE BELOW” and verify with the provided assertions. This prepares you for the competition challenge!

import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
from itertools import combinations
import math

print("Libraries loaded! Let's optimize Bean Counter's deliveries.")
Libraries loaded! Let's optimize Bean Counter's deliveries.

Section 1 - Understanding the Delivery Network

Before optimizing routes, we need to understand distances and the scale of the problem.

Bean Counter’s Franchise Locations

# Set random seed for reproducibility
np.random.seed(876)

# Generate franchise locations (x, y coordinates in km)
n_franchises = 10

# Bean Counter HQ at city center
hq_location = (2, 3)

# Generate 10 franchise locations randomly in a 10x10 km area
franchise_locations = []
for i in range(n_franchises):
    x = np.random.uniform(0.5, 9.5)
    y = np.random.uniform(0.5, 9.5)
    franchise_locations.append((x, y))

franchise_names = [
    "North District", "Northeast Corner", "East Side", "Southeast",
    "South Quarter", "Southwest", "West End", "North Central",
    "City Center East", "Inner West"
]

print(f"Bean Counter HQ: {hq_location}")
print(f"Number of franchises: {len(franchise_locations)}")
print(f"Total possible routes: {math.factorial(n_franchises):,}")
Bean Counter HQ: (2, 3)
Number of franchises: 10
Total possible routes: 3,628,800

Exercise 1.1 - Calculate Distance Between Two Points

First, let’s implement the distance calculation using the Euclidean distance formula.

TipThe Euclidean Distance Formula

The Euclidean distance between points \((x_1, y_1)\) and \((x_2, y_2)\) is: \[d = \sqrt{(x_2 - x_1)^2 + (y_2 - y_1)^2}\]

Example: Distance from (0, 0) to (3, 4) \[d = \sqrt{(3-0)^2 + (4-0)^2} = \sqrt{9 + 16} = \sqrt{25} = 5\]

NoteWorking with Tuples

A tuple is a collection of values in parentheses: point = (x, y)

# Unpacking tuple values
point1 = (5, 5)
x1, y1 = point1  # x1 = 5, y1 = 5

# Or access by index
x1 = point1[0]   # First element
y1 = point1[1]   # Second element
# YOUR CODE BELOW
def calculate_distance(point1, point2):
    """
    Calculate Euclidean distance between two points.

    Args:
        point1: Tuple (x, y) for first location
        point2: Tuple (x, y) for second location

    Returns:
        Distance in km
    """
    # Step 1: Extract x and y coordinates from both points
    
    # Step 2: Calculate differences and apply distance formula
    
    pass  # Remove this and implement
Code 
# Don't modify below - these test your solution
# Test 1: Known distance (3-4-5 triangle)
test_dist = calculate_distance((0, 0), (3, 4))
assert abs(test_dist - 5.0) < 0.001, f"Distance should be 5.0, got {test_dist}"

# Test 2: Distance to same point should be zero
same_point = calculate_distance(hq_location, hq_location)
assert abs(same_point) < 0.001, f"Distance to same point should be 0, got {same_point}"

# Test 3: Distance should be positive for different points
hq_to_first = calculate_distance(hq_location, franchise_locations[0])
assert hq_to_first > 0, f"Distance should be positive, got {hq_to_first:.2f}"

# Test 4: Distance should be symmetric
dist_a_to_b = calculate_distance(hq_location, franchise_locations[0])
dist_b_to_a = calculate_distance(franchise_locations[0], hq_location)
assert abs(dist_a_to_b - dist_b_to_a) < 0.001, "Distance should be symmetric"

print("✓ Distance calculation correct!")
print(f"HQ to first franchise: {hq_to_first:.2f} km")

Exercise 1.2 - Create Distance Matrix

Now create a matrix of all distances between locations (HQ and franchises).

TipWhat is a Distance Matrix?

A distance matrix stores all pairwise distances in a 2D array:

HQ F1 F2 F3
HQ 0 3.2 5.1 4.0
F1 3.2 0 2.8 6.1
F2 5.1 2.8 0 3.9
F3 4.0 6.1 3.9 0

distances[0][1] = distance from HQ to Franchise 1 = 3.2 km

NoteNested Loops for Matrices

Use nested for loops to fill a 2D array:

# Create 3x3 matrix
matrix = np.zeros((3, 3))

# Fill it with nested loops
for i in range(3):      # Rows
    for j in range(3):  # Columns
        matrix[i][j] = i + j

# Result: [[0, 1, 2],
#          [1, 2, 3],
#          [2, 3, 4]]
# YOUR CODE BELOW
def create_distance_matrix(hq_location, franchise_locations):
    """
    Create a distance matrix for all locations.

    Args:
        hq_location: Tuple (x, y) for HQ
        franchise_locations: List of tuples for franchises

    Returns:
        2D numpy array where element [i][j] is distance from location i to j
        Index 0 is HQ, indices 1-10 are franchises
    """
    all_locations = [hq_location] + franchise_locations
    n = len(all_locations)

    # Create empty matrix
    distances = np.zeros((n, n))

    # Fill the matrix using nested loops
    # Hint: Use your calculate_distance function!
    # Remember: distance from i to i should be 0
    # YOUR CODE HERE

    return distances
Code 
# Don't modify below - these test your solution
assert distance_matrix.shape == (11, 11), "Matrix should be 11x11 (HQ + 10 franchises)"
assert np.all(np.diag(distance_matrix) == 0), "Diagonal should be zeros (distance to self)"
assert np.allclose(distance_matrix, distance_matrix.T), "Matrix should be symmetric"
assert distance_matrix[0, 1] > 0, "HQ to first franchise distance check"
assert np.mean(distance_matrix[distance_matrix > 0]) > 3.5, "Average distance between locations check"

print("✓ Distance matrix created successfully!")
print(f"Average distance between locations: {np.mean(distance_matrix[distance_matrix > 0]):.2f} km")

Section 2 - Greedy Construction: Nearest Neighbor

Now let’s build our first route using the nearest neighbor algorithm.

Understanding Nearest Neighbor

The algorithm is simple but effective:

  1. Start at HQ
  2. Find the nearest unvisited franchise
  3. Go there and deliver
  4. Repeat until all visited
  5. Return to HQ
# Visualize Bean Counter's delivery network
plt.figure(figsize=(10, 8))

# Plot franchises
x_coords = [loc[0] for loc in franchise_locations]
y_coords = [loc[1] for loc in franchise_locations]
plt.scatter(x_coords, y_coords, c='#537E8F', s=500, zorder=3)

# Plot HQ
plt.scatter(hq_location[0], hq_location[1], c='#D73502', s=500,
           marker='s', zorder=3)

# Add labels
for i, (x, y) in enumerate(franchise_locations):
    plt.annotate(f'F{i+1}', (x, y), ha='center', va='center',
                color='white', fontweight='bold')
plt.annotate('HQ', hq_location, ha='center', va='center',
            color='white', fontweight='bold', fontsize=12)

plt.xlabel('Distance East-West (km)')
plt.ylabel('Distance North-South (km)')
plt.title("Bean Counter's Franchise Network", fontsize=14, fontweight='bold')
plt.grid(True, alpha=0.3)
plt.tight_layout()
plt.show()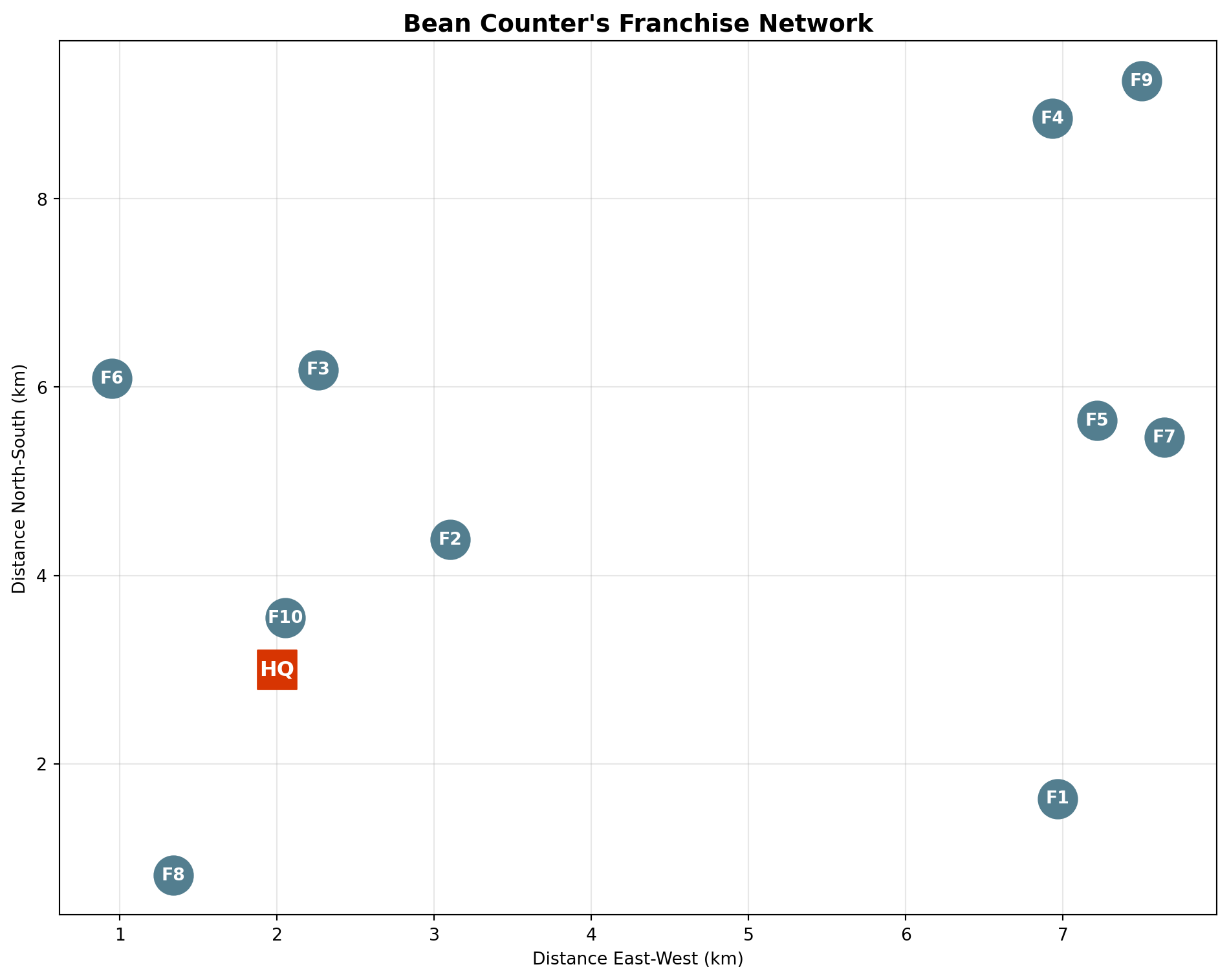

Exercise 2.1 - Implement Nearest Neighbor

Build a route using the nearest neighbor heuristic.

TipThe min() Function with key Parameter

Find the minimum based on a custom criterion:

# Find smallest number
numbers = [5, 2, 8, 1]
smallest = min(numbers)  # 1

# Find shortest word
words = ["hello", "hi", "hey"]
shortest = min(words, key=len)  # "hi"

# Find franchise with minimum distance
unvisited = [1, 2, 3]
distances_from_hq = [5.2, 3.1, 7.8]
nearest = min(unvisited, key=lambda i: distances_from_hq[i-1])  # 2

The key=lambda i: ... tells Python how to compare items.

NoteList Operations You’ll Need 
# Add to list
route.append(5)         # route = [1, 2, 3, 5]

# Remove from list
unvisited.remove(5)     # Removes value 5

# Check if list is empty
while unvisited:        # Loops while list has items
    # do something
# YOUR CODE BELOW
def nearest_neighbor_route(distance_matrix):
    """
    Build a delivery route using nearest neighbor algorithm.

    Args:
        distance_matrix: 2D array of distances (index 0 is HQ)

    Returns:
        List of franchise indices in visit order (not including HQ)
    """
    n_locations = len(distance_matrix)
    unvisited = list(range(1, n_locations))  # Franchise indices (skip 0 which is HQ)
    route = []
    current = 0  # Start at HQ

    while unvisited:
        # Step 1: Find nearest unvisited franchise using min()
        # Hint: key=lambda i: distance_matrix[current, i]
        
        # Step 2: Add it to the route
        
        # Step 3: Remove from unvisited
        
        # Step 4: Update current location
        
        pass  # Remove this

    return route
Code 
# Don't modify below - these test your solution
assert len(initial_route) == 10, "Route should visit all 10 franchises"
assert len(set(initial_route)) == 10, "Each franchise should be visited exactly once"
assert all(1 <= f <= 10 for f in initial_route), "Route should contain franchise indices 1-10"
print("✓ Nearest neighbor route constructed!")
print(f"Visit order: {initial_route}")

Exercise 2.2 - Calculate Total Route Distance

Calculate the total distance for a complete delivery route (HQ → Franchises → HQ).

# YOUR CODE BELOW
def calculate_route_distance(route, distance_matrix):
    """
    Calculate total distance for a delivery route.

    Args:
        route: List of franchise indices in visit order
        distance_matrix: 2D array of distances

    Returns:
        Total distance in km
    """
    total_distance = 0

    # Add distance from HQ to first franchise
    # YOUR CODE HERE

    # Add distances between consecutive franchises
    # YOUR CODE HERE

    # Add distance from last franchise back to HQ
    # YOUR CODE HERE

    return total_distance
    
# Calculate initial route distance
initial_distance =
Code 
# Don't modify below - these test your solution
# Test 1: Partial route should have positive distance
test_route = [1, 2, 3]
test_dist = calculate_route_distance(test_route, distance_matrix)
assert test_dist > 0, "Distance should be positive"

# Test 2: Full route distance should be reasonable (not too small, not too large)
initial_distance = calculate_route_distance(initial_route, distance_matrix)
assert initial_distance > 10, f"Total distance too small, check if return trip included: {initial_distance:.2f} km"
assert initial_distance < 150, f"Total distance too large, check calculation: {initial_distance:.2f} km"

# Test 3: Full route should be longer than partial route
assert initial_distance > test_dist, "Full route should be longer than partial route"

print(f"✓ Route distance calculation correct!")
print(f"Nearest neighbor route: {initial_distance:.2f} km")
print(f"Fuel cost: €{initial_distance * 1.5:.2f}")
print(f"Time estimate: {initial_distance / 30:.1f} hours at 30 km/h average")

Section 3 - Local Search: 2-Opt Improvement

The nearest neighbor route works, but can we improve it? Enter 2-opt!

Understanding 2-Opt Swaps

2-opt looks for crossing paths in the route and uncrosses them:

plt.figure(figsize=(10, 8))

# Create route coordinates for plotting
route_coords = [hq_location]
for idx in initial_route:
    route_coords.append(franchise_locations[idx - 1])
route_coords.append(hq_location)

# Plot route
route_x = [coord[0] for coord in route_coords]
route_y = [coord[1] for coord in route_coords]
plt.plot(route_x, route_y, 'o-', color='#A0A0A0', linewidth=2,
         markersize=0, alpha=0.7, label='Delivery Route')

# Plot locations
plt.scatter(x_coords, y_coords, c='#537E8F', s=500, zorder=3)
plt.scatter(hq_location[0], hq_location[1], c='#D73502', s=500,
           marker='s', zorder=3)

# Add labels
for i, (x, y) in enumerate(franchise_locations):
    plt.annotate(f'F{i+1}', (x, y), ha='center', va='center',
                color='white', fontweight='bold')
plt.annotate('HQ', hq_location, ha='center', va='center',
            color='white', fontweight='bold', fontsize=12)

plt.xlabel('Distance East-West (km)')
plt.ylabel('Distance North-South (km)')
plt.title(f'Initial Route: {initial_distance:.1f} km', fontsize=14, fontweight='bold')
plt.grid(True, alpha=0.3)
plt.tight_layout()
plt.show()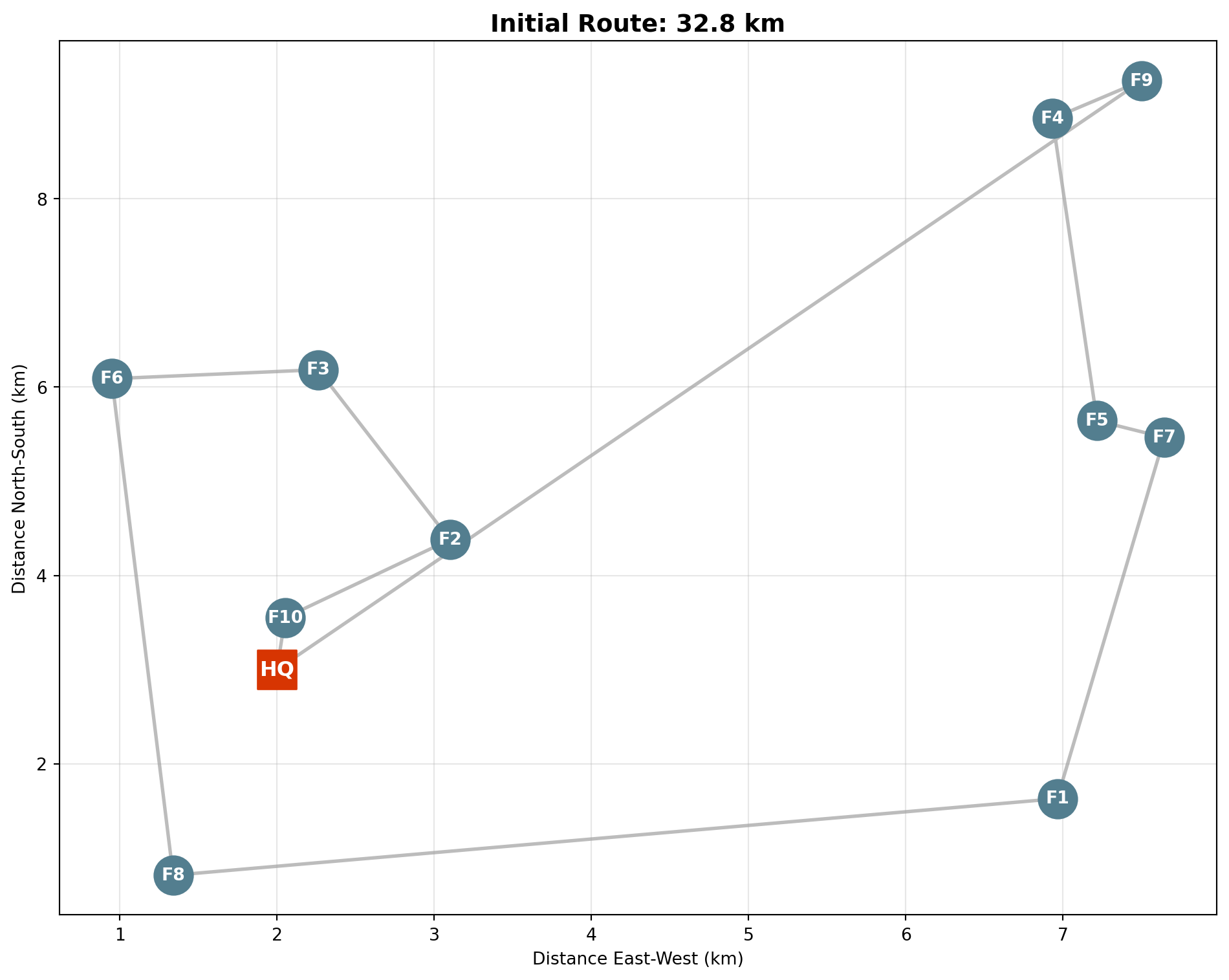

Exercise 3.1 - Implement 2-Opt Swap

Implement the logic to perform a 2-opt swap on a route.

TipWhat Does 2-Opt Do?

A 2-opt swap reverses a segment of the route to eliminate crossings:

  • Before: Route = [1, 2, 3, 4, 5, 6]
  • Swap(1, 4): Reverse segment from position 2 to 4
  • After: Route = [1, 2, 5, 4, 3, 6]

This uncrosses paths and usually reduces total distance!

NoteList Slicing and Reversal 
route = [1, 2, 3, 4, 5, 6]

# Slice: get part of list
route[:3]        # [1, 2, 3] - start to index 3
route[3:]        # [4, 5, 6] - index 3 to end
route[2:5]       # [3, 4, 5] - index 2 to 5

# Reverse: [::-1]
route[2:5][::-1] # [5, 4, 3] - reversed segment

# Combine slices
route[:2] + route[2:5][::-1] + route[5:]
# [1, 2] + [5, 4, 3] + [6] = [1, 2, 5, 4, 3, 6]
# YOUR CODE BELOW
def perform_2opt_swap(route, i, j):
    """
    Perform a 2-opt swap on a route.

    Args:
        route: Current route (list of indices)
        i: First position for swap
        j: Second position for swap (j > i)

    Returns:
        New route with the swap applied
    """
    # Create new route: beginning + reversed_middle + end
    # route[:i+1] keeps elements from start to i (inclusive)
    # route[i+1:j+1][::-1] reverses segment from i+1 to j
    # route[j+1:] keeps elements after j
    
    # YOUR CODE HERE (combine the three parts)

    pass  # Remove this
Code 
# Don't modify below - these test your solution
test_route = [1, 2, 3, 4, 5]
swapped = perform_2opt_swap(test_route, 1, 3)
assert swapped == [1, 2, 4, 3, 5], f"Expected [1, 2, 4, 3, 5], got {swapped}"

test2 = perform_2opt_swap([1, 2, 3, 4, 5, 6], 0, 4)
assert test2 == [1, 5, 4, 3, 2, 6], f"Expected [1, 5, 4, 3, 2, 6], got {test2}"

print("✓ 2-opt swap implemented correctly!")

Exercise 3.2 - Complete 2-Opt Algorithm

Now implement the full 2-opt improvement algorithm.

TipThe 2-Opt Algorithm Logic
  1. Keep trying swaps until no improvement found
  2. For each pair of positions (i, j):
    • Create new route with that swap
    • Calculate its distance
    • If better, keep it and mark improved = True
  3. Stop when a full pass finds no improvements
NoteBreaking Out of Nested Loops

When you find an improvement, you want to restart the search:

for i in range(10):
    for j in range(10):
        if found_improvement:
            improved = True
            break  # Exits inner loop
    if improved:
        break  # Exits outer loop
# Now restart the whole search
# YOUR CODE BELOW
def improve_route_2opt(route, distance_matrix, max_iterations=100):
    """
    Improve a route using 2-opt local search.

    Args:
        route: Initial route
        distance_matrix: Distance matrix
        max_iterations: Maximum improvement iterations

    Returns:
        Tuple of (improved_route, final_distance, improvement_count)
    """
    current_route = route.copy()
    current_distance = calculate_route_distance(current_route, distance_matrix)
    improvement_count = 0

    for iteration in range(max_iterations):
        improved = False

        # Try all possible 2-opt swaps
        for i in range(len(current_route) - 1):
            for j in range(i + 2, len(current_route)):
                # Step 1: Create new route with swap
                
                # Step 2: Calculate distance of new route
                
                # Step 3: If better, keep it and mark improved
                # Remember to update: current_route, current_distance, improvement_count
                
                # Step 4: Break to restart search
                
                pass  # Remove this
                
            if improved:
                break

        if not improved:
            break  # No more improvements found

    return current_route, current_distance, improvement_count
Code 
# Don't modify below - these test your solution
assert len(improved_route) == 10, "Improved route should still visit all franchises"
assert improved_distance <= initial_distance, "Distance shouldn't increase"
assert improvements >= 0, "Should track improvements"

improvement_pct = (initial_distance - improved_distance) / initial_distance * 100
print(f"✓ 2-opt improvement complete!")
print(f"Initial distance: {initial_distance:.2f} km")
print(f"Improved distance: {improved_distance:.2f} km")
print(f"Improvement: {improvement_pct:.1f}% ({improvements} swaps)")
print(f"Monthly savings: €{(initial_distance - improved_distance) * 1.5 * 20:.2f}")

Section 4 - Comparing Different Initial Solutions

Different starting points can lead to different final solutions. Let’s explore!

Exercise 4.1 - Random Initial Route

Create a random initial route and see if 2-opt can improve it.

# YOUR CODE BELOW
def create_random_route(n_franchises):
    """
    Create a random delivery route.

    Args:
        n_franchises: Number of franchises

    Returns:
        Random route (list of indices 1 to n_franchises)
    """
    # Create list [1, 2, ..., n_franchises] and shuffle it
    # YOUR CODE HERE

    pass  # Remove this

# Create and improve random route
random_route = create_random_route(10)
random_distance = calculate_route_distance(random_route, distance_matrix)

# Improve it with 2-opt
random_improved, random_final_dist, random_swaps = improve_route_2opt(
    random_route, distance_matrix
)
Code 
# Don't modify below - these test your solution
assert len(random_route) == 10, "Random route should have 10 franchises"
assert set(random_route) == set(range(1, 11)), "Should contain franchises 1-10"
assert random_final_dist <= random_distance, "2-opt shouldn't make it worse"

print(f"✓ Random route analysis complete!")
print(f"Random initial: {random_distance:.2f} km")
print(f"After 2-opt: {random_final_dist:.2f} km")
print(f"Improvements: {random_swaps} swaps")

Exercise 4.2 - Multiple Random Starts

Try multiple random starting points to find the best solution.

# YOUR CODE BELOW
def multi_start_optimization(distance_matrix, n_starts=10):
    """
    Run 2-opt from multiple random starting points.

    Args:
        distance_matrix: Distance matrix
        n_starts: Number of random starts to try

    Returns:
        Best route found and its distance
    """
    best_route = None
    best_distance = float('inf')

    for i in range(n_starts):
        # Create random initial route
        # YOUR CODE HERE

        # Improve with 2-opt
        # YOUR CODE HERE

        # Keep if best so far
        # YOUR CODE HERE

        pass  # Remove this

    return best_route, best_distance

# Try multi-start optimization
multi_route, multi_distance = multi_start_optimization(distance_matrix, n_starts=20)
Code 
# Don't modify below - these test your solution
assert len(multi_route) == 10, "Best route should have 10 franchises"
assert multi_distance <= improved_distance, "Multi-start shouldn't be worse than single"

print(f"✓ Multi-start optimization complete!")
print(f"Best distance found: {multi_distance:.2f} km")
print(f"vs. Nearest Neighbor + 2-opt: {improved_distance:.2f} km")
print(f"vs. Random + 2-opt: {random_final_dist:.2f} km")

Section 5 - Making the CEO Decision

As CEO, you need to choose the best approach for Bean Counter’s deliveries.

Visualizing All Solutions

# Compare all approaches
plt.figure(figsize=(14, 10))

# Define all routes and methods for comparison
routes = [
    (initial_route, initial_distance, "Nearest Neighbor", '#A0A0A0'),
    (improved_route, improved_distance, "NN + 2-Opt", '#537E8F'),
    (random_route, random_distance, "Random Initial", '#F4A582'),
    (random_improved, random_final_dist, "Random + 2-Opt", '#92C5DE'),
    (multi_route, multi_distance, "Multi-Start Best", '#D73502')
]

# Create subplots
for idx, (route, distance, title, color) in enumerate(routes[:4], 1):
    plt.subplot(2, 2, idx)

    # Create route coordinates
    route_coords = [hq_location]
    for r_idx in route:
        route_coords.append(franchise_locations[r_idx - 1])
    route_coords.append(hq_location)

    # Plot route
    route_x = [coord[0] for coord in route_coords]
    route_y = [coord[1] for coord in route_coords]
    plt.plot(route_x, route_y, 'o-', color=color, linewidth=2,
             markersize=0, alpha=0.7)

    # Plot locations
    plt.scatter(x_coords, y_coords, c='#537E8F', s=100, zorder=3)
    plt.scatter(hq_location[0], hq_location[1], c='#D73502',
               s=200, marker='s', zorder=3)

    plt.title(f'{title}: {distance:.1f} km', fontweight='bold')
    plt.grid(True, alpha=0.3)

plt.tight_layout()
plt.suptitle('Bean Counter Delivery Route Comparison', fontsize=14, fontweight='bold', y=1.02)
plt.show()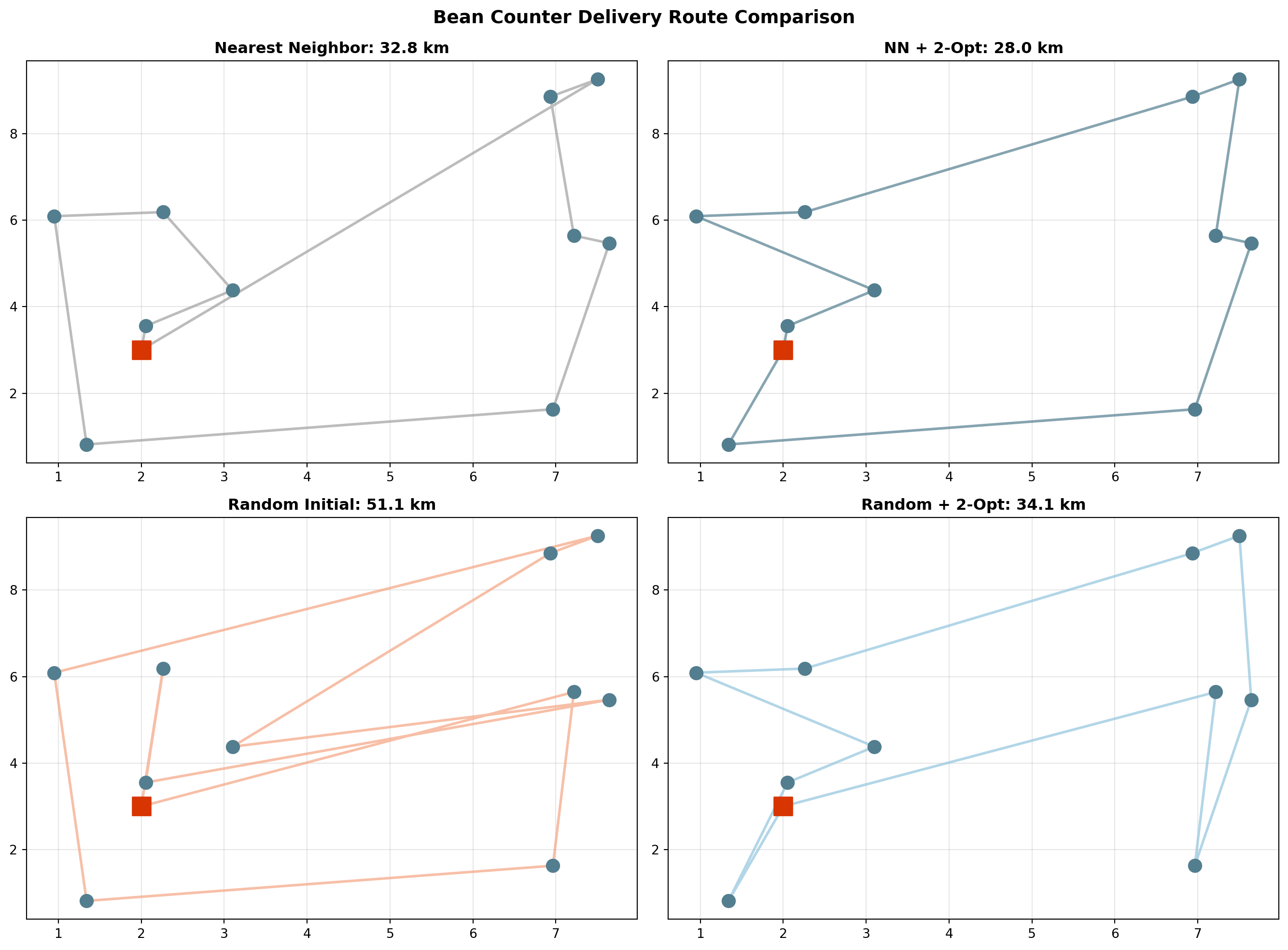

Exercise 5.1 - Performance Summary

Create a summary comparing all approaches.

# YOUR CODE BELOW
def create_performance_summary(methods_data):
    """
    Create a performance summary DataFrame.

    Args:
        methods_data: List of tuples (method_name, distance, time_hours)

    Returns:
        DataFrame with performance metrics
    """
    # Create DataFrame with columns: Method, Distance, Fuel Cost, Time, Labor Cost, Total Cost
    # YOUR CODE HERE

    pass  # Remove this

# Prepare data (assuming 30 km/h average speed)
methods_data = [
    ("Nearest Neighbor", initial_distance),
    ("NN + 2-Opt", improved_distance),
    ("Random Initial", random_distance),
    ("Random + 2-Opt", random_final_dist),
    ("Multi-Start", multi_distance)
]

# Create summary
summary_df = create_performance_summary(methods_data)
Code 
# Don't modify below - these test your solution
# Test 1: Should have all 5 methods
assert len(summary_df) == 5, "Should have 5 methods"

# Test 2: Should have required columns
assert 'Total Cost (€)' in summary_df.columns, "Should calculate total cost"
assert 'Distance (km)' in summary_df.columns, "Should have distance"

# Test 3: Costs should be positive and reasonable
assert summary_df['Total Cost (€)'].min() > 0, "Costs should be positive"
assert summary_df['Total Cost (€)'].max() < 500, "Costs should be reasonable (< €500)"

# Test 4: Best method should beat worst method
best_cost = summary_df['Total Cost (€)'].min()
worst_cost = summary_df['Total Cost (€)'].max()
assert best_cost < worst_cost, "Best method should have lower cost than worst"

best_method = summary_df.loc[summary_df['Total Cost (€)'].idxmin(), 'Method']
best_savings = worst_cost - best_cost

print(f"\n✓ CEO Decision Summary Complete!")
print(f"Best method: {best_method}")
print(f"Daily savings vs worst: €{best_savings:.2f}")
print(f"Annual savings: €{best_savings * 250:.2f} (250 delivery days)")

Final CEO Recommendation

# Create final recommendation visualization
fig, (ax1, ax2) = plt.subplots(1, 2, figsize=(14, 5))

# Cost comparison bar chart
methods = [m[0] for m in methods_data]
distances = [m[1] for m in methods_data]
costs = [d * 1.50 + (d/30) * 30 for d in distances]

ax1.bar(range(len(methods)), costs, color=['#A0A0A0', '#537E8F', '#F4A582', '#92C5DE', '#D73502'])
ax1.set_xticks(range(len(methods)))
ax1.set_xticklabels(methods, rotation=45, ha='right')
ax1.set_ylabel('Total Cost per Day (€)')
ax1.set_title('Daily Delivery Cost Comparison', fontweight='bold')
ax1.grid(True, alpha=0.3, axis='y')

# Improvement over time
baseline = costs[0]
savings = [baseline - c for c in costs]
months = range(1, 13)
cumulative_savings = [s * 20 * m for m in months for s in [savings[1]]]  # Using NN+2-opt

ax2.plot(months, cumulative_savings, 'o-', color='#537E8F', linewidth=2.5, markersize=8)
ax2.fill_between(months, 0, cumulative_savings, alpha=0.3, color='#537E8F')
ax2.set_xlabel('Months')
ax2.set_ylabel('Cumulative Savings (€)')
ax2.set_title('Projected Annual Savings with Optimization', fontweight='bold')
ax2.grid(True, alpha=0.3)

plt.tight_layout()
plt.show()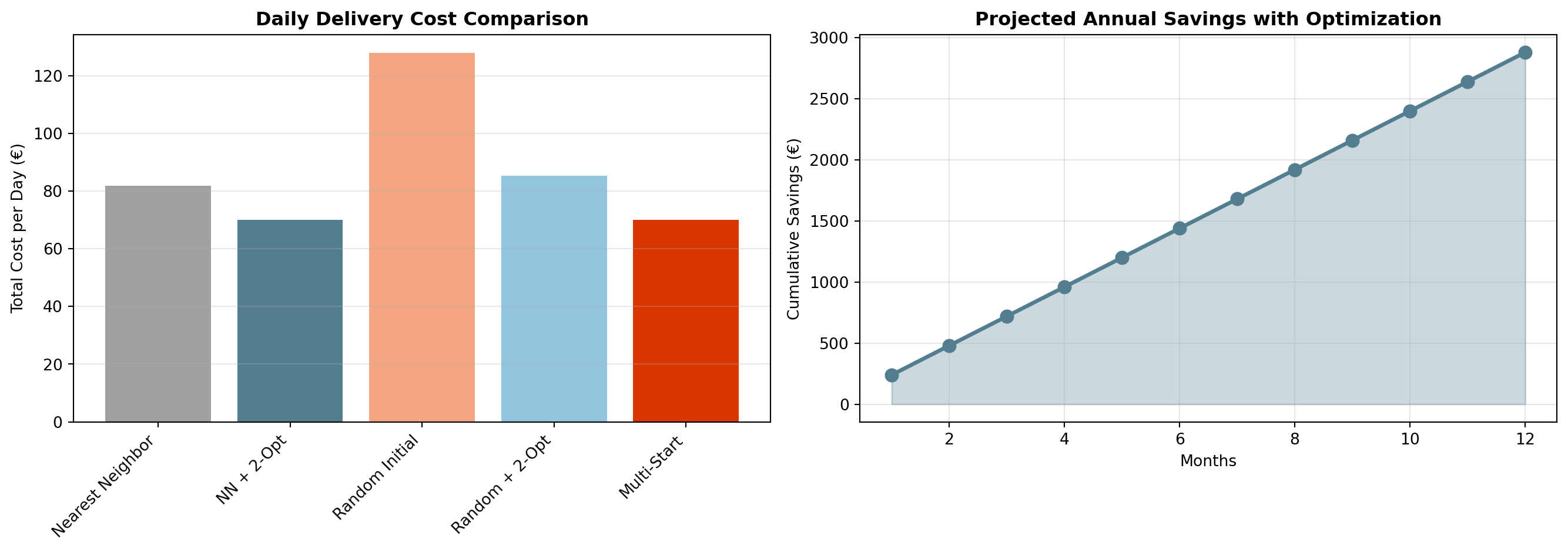

Conclusion

Congratulations! You’ve learned the fundamentals of route optimization and local search!

Key Takeaways

  1. The Traveling Salesman Problem (TSP):
    • Visiting all locations with minimum distance
    • Exact solutions impractical for real-world problems
  2. Greedy Construction Algorithms:
    • Nearest Neighbor: Fast, simple, decent quality
    • Start somewhere, always go to closest unvisited location
    • Quick to implement and understand
  3. Local Search Improvement:
    • 2-opt: Systematically uncross routes to reduce distance
    • Converges to local optimum (best among nearby solutions)
    • Simple yet powerful optimization technique
  4. Multi-start Strategy:
    • Different starting points → different local optima
    • Random starts help explore solution space
    • Best found solution often much better than single attempt
  5. Algorithm Performance:
    • Nearest Neighbor: Quick construction, reasonable results
    • NN + 2-Opt: Balanced approach, more improvement possible
    • Choice depends on time constraints and quality needs!
  6. Business Impact:
    • Route optimization delivers immediate, measurable savings
    • Better routes = lower fuel costs + faster deliveries
    • Scales to much larger real-world delivery networks

What’s Next?

You’ve now mastered the core concepts of routing optimization! In the Artisan Bakery Competition, you’ll apply these techniques to a more challenging problem with:

  • 16 cafés (vs. 10 franchises)
  • Time window constraints (early deliveries required!)

In future lectures, you’ll learn advanced techniques like metaheuristics (simulated annealing, genetic algorithms, tabu search) that can escape local optima and find even better solutions by intelligently exploring the solution space.

Your Bean Counter deliveries are now optimized. Time to help the bakery!