Management Science - Two-Stage Scheduling Competition
Custom Cycles Manufacturing is a premium bicycle manufacturer based in Hamburg, Germany. Founded in 1998, they’ve built a reputation for high-quality custom builds with a loyal customer base of cycling enthusiasts and professional riders. Annual revenue: 8.5M with 35% coming from holiday rush orders.
Your Role: You’ve been hired as the weekend operations manager to handle a critical scheduling crisis.
It’s Friday at 06:00 in the morning. The production manager just quit unexpectedly, leaving you with a major problem:
CEO’s Message: “We can’t afford to lose these customers before the holiday season. Figure out the optimal schedule and minimize our costs. Our reputation depends on it!”
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import matplotlib.patches as mpatches
# Set random seed for reproducibility
np.random.seed(2025)
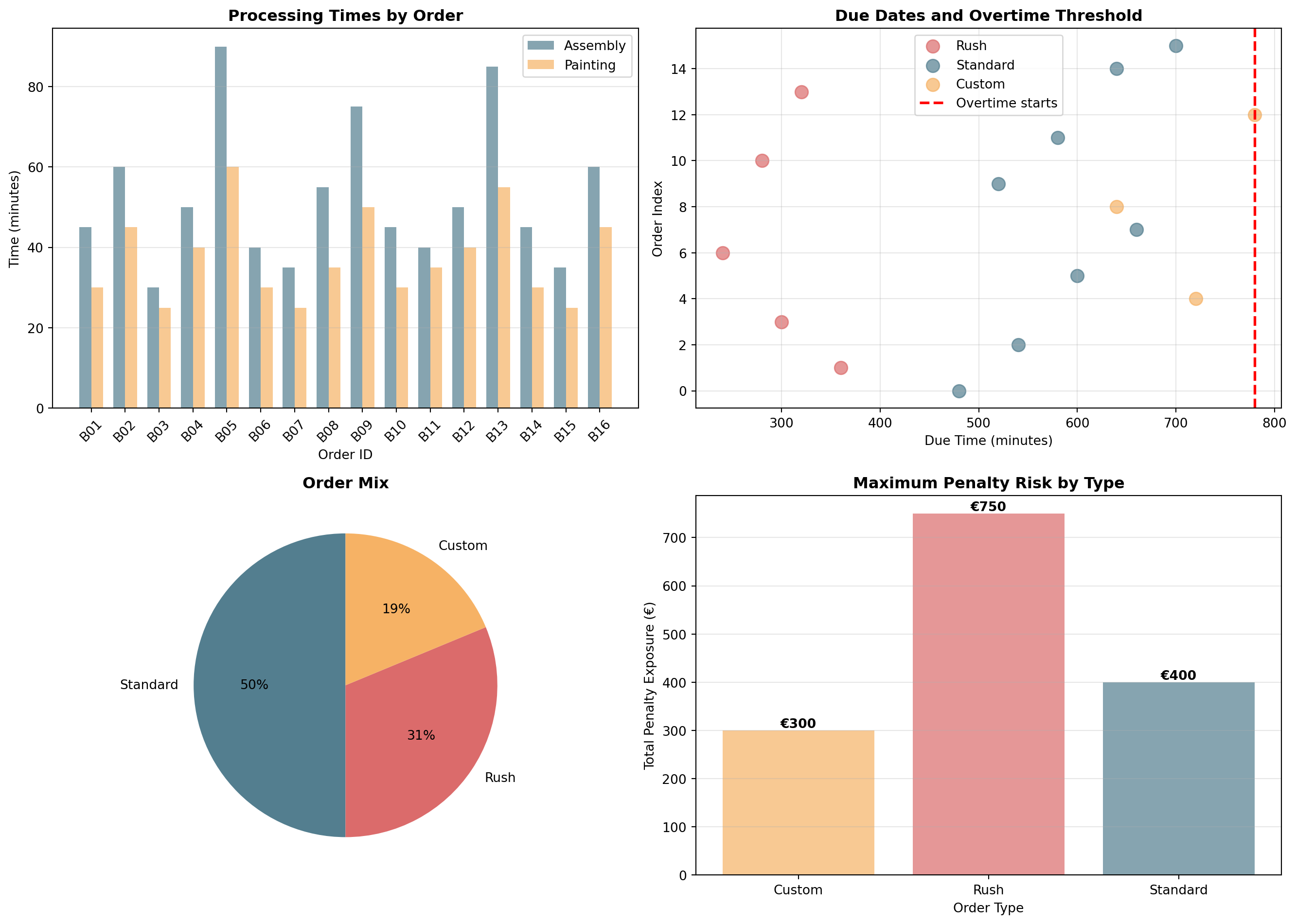
print("Libraries loaded! Ready to tackle the bike factory crisis.")Libraries loaded! Ready to tackle the bike factory crisis.# DON'T MODIFY THIS DATA - These are your actual orders!
bike_orders = [
{'id': 'B01', 'type': 'Standard', 'assembly': 45, 'painting': 30, 'due': 480, 'penalty': 50},
{'id': 'B02', 'type': 'Rush', 'assembly': 60, 'painting': 45, 'due': 360, 'penalty': 150},
{'id': 'B03', 'type': 'Standard', 'assembly': 30, 'painting': 25, 'due': 540, 'penalty': 50},
{'id': 'B04', 'type': 'Rush', 'assembly': 50, 'painting': 40, 'due': 300, 'penalty': 150},
{'id': 'B05', 'type': 'Custom', 'assembly': 90, 'painting': 60, 'due': 720, 'penalty': 100},
{'id': 'B06', 'type': 'Standard', 'assembly': 40, 'painting': 30, 'due': 600, 'penalty': 50},
{'id': 'B07', 'type': 'Rush', 'assembly': 35, 'painting': 25, 'due': 240, 'penalty': 150},
{'id': 'B08', 'type': 'Standard', 'assembly': 55, 'painting': 35, 'due': 660, 'penalty': 50},
{'id': 'B09', 'type': 'Custom', 'assembly': 75, 'painting': 50, 'due': 640, 'penalty': 100},
{'id': 'B10', 'type': 'Standard', 'assembly': 45, 'painting': 30, 'due': 520, 'penalty': 50},
{'id': 'B11', 'type': 'Rush', 'assembly': 40, 'painting': 35, 'due': 280, 'penalty': 150},
{'id': 'B12', 'type': 'Standard', 'assembly': 50, 'painting': 40, 'due': 580, 'penalty': 50},
{'id': 'B13', 'type': 'Custom', 'assembly': 85, 'painting': 55, 'due': 780, 'penalty': 100},
{'id': 'B14', 'type': 'Rush', 'assembly': 45, 'painting': 30, 'due': 320, 'penalty': 150},
{'id': 'B15', 'type': 'Standard', 'assembly': 35, 'painting': 25, 'due': 640, 'penalty': 50},
{'id': 'B16', 'type': 'Standard', 'assembly': 60, 'painting': 45, 'due': 700, 'penalty': 50}
]
# Convert to DataFrame for analysis
df_bikes = pd.DataFrame(bike_orders)
print("Custom Cycles - Rush Orders")
print("=" * 50)
print(f"Total orders: {len(df_bikes)}")
print(f"\nOrder breakdown by type:")
print(df_bikes['type'].value_counts().to_string())
print(f"\nWorkload analysis:")
print(f" Total assembly time: {df_bikes['assembly'].sum()} minutes ({df_bikes['assembly'].sum()/60:.1f} hours)")
print(f" Total painting time: {df_bikes['painting'].sum()} minutes ({df_bikes['painting'].sum()/60:.1f} hours)")
print(f" Average assembly: {df_bikes['assembly'].mean():.1f} minutes")
print(f" Average painting: {df_bikes['painting'].mean():.1f} minutes")
print(f"\nTime constraints:")
print(f" Work starts: Friday 6:00 (minute 0)")
print(f" Regular hours end: Friday 19:00 (minute 780)")
print(f" Overtime rate: €100/hour after minute 780")
print(f"\nPenalty exposure:")
print(f" Total if ALL orders late: €{df_bikes['penalty'].sum():,}")
# DON'T MODIFY ABOVE!Custom Cycles - Rush Orders
==================================================
Total orders: 16
Order breakdown by type:
type
Standard 8
Rush 5
Custom 3
Workload analysis:
Total assembly time: 840 minutes (14.0 hours)
Total painting time: 600 minutes (10.0 hours)
Average assembly: 52.5 minutes
Average painting: 37.5 minutes
Time constraints:
Work starts: Friday 6:00 (minute 0)
Regular hours end: Friday 19:00 (minute 780)
Overtime rate: €100/hour after minute 780
Penalty exposure:
Total if ALL orders late: €1,450# Visualize order characteristics
fig, axes = plt.subplots(2, 2, figsize=(14, 10))
# 1. Processing times by order
ax = axes[0, 0]
x = np.arange(len(df_bikes))
width = 0.35
ax.bar(x - width/2, df_bikes['assembly'], width, label='Assembly', color='#537E8F', alpha=0.7)
ax.bar(x + width/2, df_bikes['painting'], width, label='Painting', color='#F6B265', alpha=0.7)
ax.set_xlabel('Order ID')
ax.set_ylabel('Time (minutes)')
ax.set_title('Processing Times by Order', fontweight='bold')
ax.set_xticks(x)
ax.set_xticklabels(df_bikes['id'], rotation=45)
ax.legend()
ax.grid(axis='y', alpha=0.3)
# 2. Due dates timeline
ax = axes[0, 1]
colors = {'Rush': '#DB6B6B', 'Standard': '#537E8F', 'Custom': '#F6B265'}
for order_type in ['Rush', 'Standard', 'Custom']:
subset = df_bikes[df_bikes['type'] == order_type]
ax.scatter(subset['due'], subset.index, label=order_type,
color=colors[order_type], s=100, alpha=0.7)
ax.axvline(x=780, color='red', linestyle='--', label='Overtime starts', linewidth=2)
ax.set_xlabel('Due Time (minutes)')
ax.set_ylabel('Order Index')
ax.set_title('Due Dates and Overtime Threshold', fontweight='bold')
ax.legend()
ax.grid(alpha=0.3)
# 3. Order type distribution
ax = axes[1, 0]
type_counts = df_bikes['type'].value_counts()
colors_pie = [colors[t] for t in type_counts.index]
ax.pie(type_counts.values, labels=type_counts.index, autopct='%1.0f%%',
colors=colors_pie, startangle=90)
ax.set_title('Order Mix', fontweight='bold')
# 4. Penalty distribution
ax = axes[1, 1]
penalty_by_type = df_bikes.groupby('type')['penalty'].agg(['sum', 'mean', 'count'])
x_pos = np.arange(len(penalty_by_type))
ax.bar(x_pos, penalty_by_type['sum'], color=[colors[t] for t in penalty_by_type.index], alpha=0.7)
ax.set_xlabel('Order Type')
ax.set_ylabel('Total Penalty Exposure (€)')
ax.set_title('Maximum Penalty Risk by Type', fontweight='bold')
ax.set_xticks(x_pos)
ax.set_xticklabels(penalty_by_type.index)
ax.grid(axis='y', alpha=0.3)
# Add value labels
for i, v in enumerate(penalty_by_type['sum']):
ax.text(i, v, f'€{v:.0f}', ha='center', va='bottom', fontweight='bold')
plt.tight_layout()
plt.show()
print("\nKey Insights:")
print(f" - Tightest deadline: Order {df_bikes.loc[df_bikes['due'].idxmin(), 'id']} (due at {df_bikes['due'].min()} min)")
print(f" - Longest processing: Order {df_bikes.loc[(df_bikes['assembly']+df_bikes['painting']).idxmax(), 'id']} ({(df_bikes['assembly']+df_bikes['painting']).max()} min total)")
print(f" - Rush orders have {df_bikes[df_bikes['type']=='Rush']['penalty'].iloc[0]/df_bikes[df_bikes['type']=='Standard']['penalty'].iloc[0]:.0f}x higher penalties")
Key Insights:
- Tightest deadline: Order B07 (due at 240 min)
- Longest processing: Order B05 (150 min total)
- Rush orders have 3x higher penaltiesdef calculate_schedule_cost(schedule, overtime_threshold=780, overtime_rate_per_min=100/60):
"""
Calculate total cost for a given schedule
Parameters:
- schedule: list of orders with completion times
- overtime_threshold: minute when overtime starts (default 780)
- overtime_rate_per_min: cost per minute of overtime (default €1.67/min)
Returns:
- Dictionary with cost breakdown
"""
total_overtime_cost = 0
total_penalty_cost = 0
late_orders = []
for order in schedule:
# Check for overtime (based on painting end time)
if order['painting_end'] > overtime_threshold:
overtime_minutes = order['painting_end'] - overtime_threshold
overtime_cost = overtime_minutes * overtime_rate_per_min
total_overtime_cost += overtime_cost
# Check for late delivery
if order['completion'] > order['due']:
total_penalty_cost += order['penalty']
late_orders.append(order['id'])
return {
'total_cost': total_overtime_cost + total_penalty_cost,
'overtime_cost': total_overtime_cost,
'penalty_cost': total_penalty_cost,
'late_count': len(late_orders),
'late_orders': late_orders
}
def two_stage_schedule(orders, sequence):
"""
Schedule orders through assembly and painting stations
Parameters:
- orders: list of order dictionaries
- sequence: list of order IDs in desired processing order
Returns:
- scheduled_orders: list with start/end times added
"""
# Create a copy and reorder based on sequence
order_dict = {o['id']: o.copy() for o in orders}
scheduled_orders = [order_dict[oid] for oid in sequence]
assembly_time = 0
painting_time = 0
for order in scheduled_orders:
# Assembly station (starts immediately when available)
order['assembly_start'] = assembly_time
order['assembly_end'] = assembly_time + order['assembly']
assembly_time = order['assembly_end']
# Painting station (must wait for both: painting available AND assembly done)
order['painting_start'] = max(painting_time, order['assembly_end'])
order['painting_end'] = order['painting_start'] + order['painting']
painting_time = order['painting_end']
# Overall completion is when painting finishes
order['completion'] = order['painting_end']
return scheduled_orders
print("Helper functions loaded!")
print("\nAvailable functions:")
print(" - calculate_schedule_cost(schedule) → cost breakdown")
print(" - two_stage_schedule(orders, sequence) → scheduled orders with times")Helper functions loaded!
Available functions:
- calculate_schedule_cost(schedule) → cost breakdown
- two_stage_schedule(orders, sequence) → scheduled orders with times# Example: Schedule in original order (FIFO approach)
print("Example: FIFO Schedule (Original Order)")
# Create sequence in original order
fifo_sequence = [o['id'] for o in bike_orders]
print(f"Order sequence: {fifo_sequence}")
# Schedule the orders (function just takes the schedule created)
# Hint: Print `fifo_sequence` to see what's expected for the function to work
fifo_schedule = two_stage_schedule(bike_orders, fifo_sequence)
# Calculate costs (this)
fifo_costs = calculate_schedule_cost(fifo_schedule)
print(f"\nResults:")
print(f" Total Cost: €{fifo_costs['total_cost']:.2f}")
print(f" Breakdown:")
print(f" - Overtime: €{fifo_costs['overtime_cost']:.2f}")
print(f" - Penalties: €{fifo_costs['penalty_cost']:.2f}")
print(f" Late orders: {fifo_costs['late_count']} out of {len(bike_orders)}")
print(f" Final completion: {fifo_schedule[-1]['completion']} minutes ({fifo_schedule[-1]['completion']/60:.1f} hours)")
print("\nThis is just ONE possible schedule. Can you do better?")Example: FIFO Schedule (Original Order)
Order sequence: ['B01', 'B02', 'B03', 'B04', 'B05', 'B06', 'B07', 'B08', 'B09', 'B10', 'B11', 'B12', 'B13', 'B14', 'B15', 'B16']
Results:
Total Cost: €883.33
Breakdown:
- Overtime: €233.33
- Penalties: €650.00
Late orders: 7 out of 16
Final completion: 885 minutes (14.8 hours)
This is just ONE possible schedule. Can you do better?Before coding, think through these questions:
Try multiple approaches and compare them to select the best one.
# YOUR SOLUTION HERE# Create Gantt chart for your best solution
# YOUR SOLUTION HEREPrepare a one-slide presentation (PDF) containing: