Lecture 4 - Management Science
. . .
CEO’s Dilemma:
“We have €2M to invest in 2 of 4 startups. Each promises great returns, but the future is uncertain. How do we make the best choice without just gambling?”
Question: Why can’t we just pick the two startups with the highest average returns?
. . .
. . .
Common Pitfall: Optimizing on averages ignores the distribution of outcomes.
Where uncertainty modeling is critical:
Netflix Series Decisions
Pharmaceutical R&D
. . .
When decisions are expensive and outcomes are uncertain, Monte Carlo simulation can be helpful to reduce risk and maximize value!
Question: If you roll two dice, what’s the probability of getting exactly 7 as result?
. . .
Method 1: Math
Question: If you roll two dice, what’s the probability of getting exactly 7 as result?
. . .
Method 2: Simulation
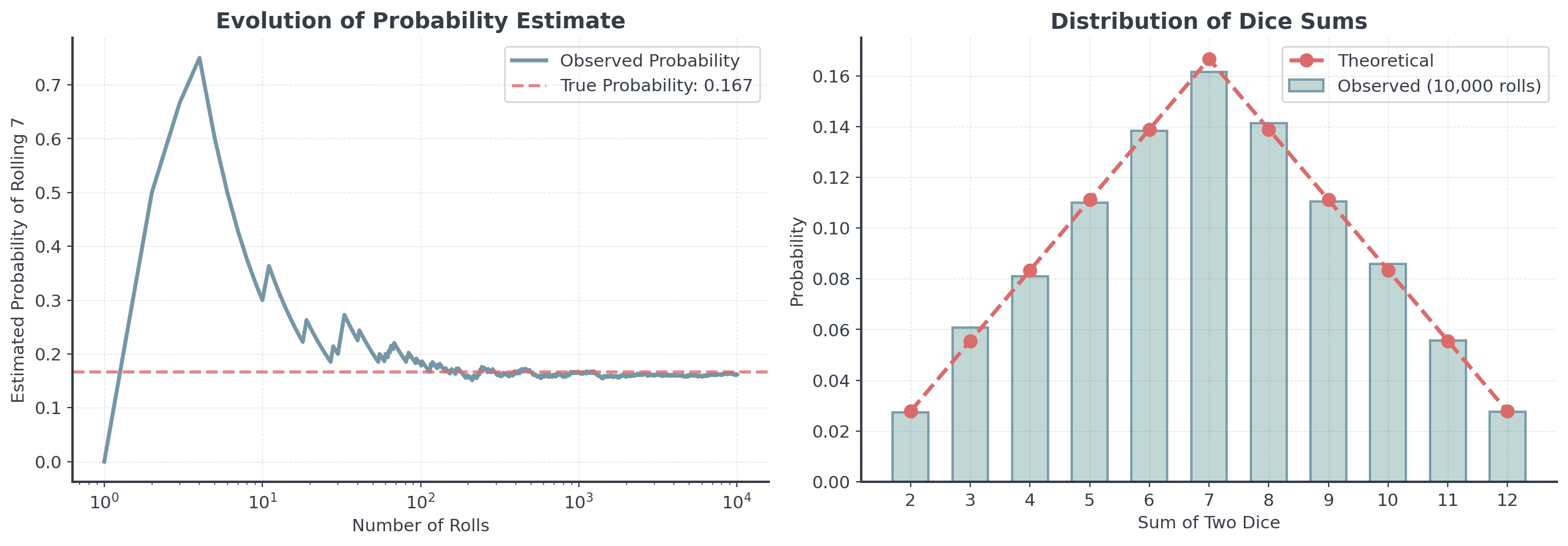
import numpy as np
np.random.seed(42)
# Roll two dice 10,000 times
dice1 = np.random.randint(1, 7, size=10_000)
dice2 = np.random.randint(1, 7, size=10_000)
total = dice1 + dice2
# What fraction equals 7?
probability = (total == 7).mean()
print(f"Simulated probability of rolling 7: {probability:.1%}")Simulated probability of rolling 7: 16.2%
. . .
As we roll more dice, the estimated probability converges to the true value (16.7%)
Fundamental Principle: As sample size increases, sample average converges to the true expected value
. . .
If \(X_1, X_2, \ldots, X_n\) are independent random samples from the same distribution with mean \(\mu\):
\[\text{As } n \to \infty, \quad \bar{X}_n = \frac{1}{n}\sum_{i=1}^n X_i \to \mu\]
. . .
This is WHY simulations works. More simulations = better estimates!
Another Fundamental Principle: The sum of many random variables tends toward a normal distribution
. . .
What it means:
. . .
For Business: This is why we can use normal distributions to model portfolio returns, even when individual assets have skewed or unusual distributions!
Question: How many simulations do we need for reliable results?
. . .
# Test convergence with different sample sizes
sample_sizes = [10, 100, 1000, 10000, 100000]
estimates = []
for n in sample_sizes:
dice1 = np.random.randint(1, 7, size=n)
dice2 = np.random.randint(1, 7, size=n)
total = dice1 + dice2
prob = (total == 7).mean()
estimates.append(prob)
print(f"n={n:6d}: Estimated probability = {prob:.4f}")n= 10: Estimated probability = 0.2000
n= 100: Estimated probability = 0.1900
n= 1000: Estimated probability = 0.1480
n= 10000: Estimated probability = 0.1652
n=100000: Estimated probability = 0.1670How many simulations should you run?
. . .
If your decision changes with 10x more simulations, you didn’t run enough!
Three Simple Steps:
. . .
Monte Carlo Casino in Monaco inspired the method’s development in the 1940s.
Key Function: np.random.normal(loc, scale, size)
. . .
# AI-Growth: average 38% return, ±25% volatility
returns = np.random.normal(loc=0.38, scale=0.25, size=10_000)
print(f"Mean return: {returns.mean():.1%}")
print(f"Std deviation: {returns.std():.1%}")
print(f"Minimum: {returns.min():.1%}")
print(f"Maximum: {returns.max():.1%}")Mean return: 38.8%
Std deviation: 24.8%
Minimum: -67.0%
Maximum: 125.7%Let’s calculate percentiles with np.percentile().
. . .
Question: Do you still know what a percentile is?
. . .
print(f"\nPercentiles:")
print(f" 5th: {np.percentile(returns, 5):.1%} (worst 5% of scenarios)")
print(f" 25th: {np.percentile(returns, 25):.1%} (worst 25% of scenarios)")
print(f" 50th: {np.percentile(returns, 50):.1%} (median)")
print(f" 75th: {np.percentile(returns, 75):.1%} (best 25% of scenarios)")
print(f" 95th: {np.percentile(returns, 95):.1%} (best 5% of scenarios)")
Percentiles:
5th: -2.7% (worst 5% of scenarios)
25th: 22.1% (worst 25% of scenarios)
50th: 38.9% (median)
75th: 55.7% (best 25% of scenarios)
95th: 78.6% (best 5% of scenarios)Question: Before we plot, what shape do you expect for np.random.normal()?
. . .
Question: What’s the probability that AI-Growth loses money?
. . .
# Calculate risk metrics
prob_loss = (returns < 0).mean() # proportion of returns that are less than zero
prob_double = (returns > 1.0).mean() # proportion greater than 100%
print(f"Probability of loss: {prob_loss:.1%}")
print(f"Probability of doubling money: {prob_double:.1%}")Probability of loss: 6.0%
Probability of doubling money: 0.8%. . .
With 6 % chance of loss, AI-Growth is relatively safe. Easy for one startup, right?
Attention: Not everything follows a normal distribution!
# Most common in nature/business
# Bell-shaped, symmetric
returns = np.random.normal(mean, std, size)
# Example: CloudAI startup returns
cloudai = np.random.normal(0.25, 0.15, 10000) # 25% ± 15%Main Characteristics:
# Equal probability across range
# Example: FinFlow returns between 10-35%
returns = np.random.uniform(0.10, 0.35, size)
# Example: FinFlow startup returns
finflow = np.random.uniform(0.10, 0.35, 10000) # 10-35% equally likelyMain Characteristics:
# Time between events
# Example: Customer arrivals, equipment failure
times = np.random.exponential(scale, size)
# Example: Time between customer arrivals (minutes)
arrivals = np.random.exponential(5, 10000) # Average 5 minutesMain Characteristics:
Suppose we have the following startups:
CloudAI, GreenGrid, HealthTrack, FinFlow
. . .
Question: If we must pick 2 of 4, how many unique pairs exist?
. . .
The Math:
\[\binom{4}{2} = \frac{4!}{2! \times 2!} = \frac{4 \times 3 \times 2 \times 1}{(2 \times 1) \times (2 \times 1)} = \frac{24}{4} = 6\]
. . .
Each combination has different risk-return characteristics!
. . .
Question: Which startup is the best choice?
Question: Which metrics matter most for investment decisions?
. . .
No metric tells the whole story. Investors consider multiple dimensions of risk and return.
Tail Risk: The danger lurking in worst-case scenarios
Expected Shortfall (ES)
. . .
A portfolio with higher average returns might have catastrophic tail risk. Always look at the extremes!
So far, we’ve assumed startups succeed or fail independently.
. . .
Independent Events:
. . .
Question: Is this realistic in the real world?
. . .
Reality Check: Many business risks are correlated! Economic downturns, market trends, and technology shifts affect multiple companies simultaneously.
Correlation measures how two variables move together.
\[\rho_{X,Y} = \frac{\text{Cov}(X,Y)}{\sigma_X \sigma_Y} \quad \text{where } -1 \leq \rho \leq 1\]
. . .
Interpreting Correlation:
. . .
In Python: np.corrcoef(returns1, returns2) calculates correlation
Two AI startups in your portfolio:
Scenario 1: Independent (ρ = 0)
Scenario 2: Positively Correlated (ρ = 0.8)
. . .
Diversification only reduces risk when investments are not highly correlated!
. . .
Higher correlation = Wider distribution = More risk!
Common sources of correlation in business:
. . .
Diversification: Choose investments with LOW correlation to reduce portfolio risk!
. . .
2008 Financial Crisis: Many “diversified” portfolios collapsed due to correlations!
Question: For our simple startup examples so far, do we really NEED Monte Carlo?
. . .
Short answer: No! For basic mean/variance calculations, we can use analytical formulas.
. . .
So when is Monte Carlo truly necessary?
You can use math (analytical solutions):
. . .
You NEED Monte Carlo when:
Where Monte Carlo is ESSENTIAL, not just convenient:
1. Option Pricing with Path Dependencies
# Payoff depends on AVERAGE price over time
n_simulations = 10000; strike_price = 105; payoffs = []
for sim in range(n_simulations):
prices = [100] # Starting price
for day in range(365):
prices.append(prices[-1] * (1 + np.random.normal(0.001, 0.02)))
payoff = max(0, np.mean(prices) - strike_price)
payoffs.append(payoff)
payoffs = np.array(payoffs)
print(f"Average option value: ${payoffs.mean():.2f}")
print(f"Probability of profit: {(payoffs > 0).mean():.1%}")Average option value: $19.58
Probability of profit: 68.9%
2. Supply Chain with Cascading Effects
# Each stage affects the next (nonlinear dependencies)
n_simulations = 10000; factory_capacity = 150; demand = 120; price = 5
penalty = 10; revenues = []
for sim in range(n_simulations):
parts_delivered = np.random.poisson(100)
production = min(parts_delivered, factory_capacity)
if production >= demand:
revenue = demand * price
else:
revenue = production * price - penalty
revenues.append(revenue)
revenues = np.array(revenues)
print(f"Average revenue: ${revenues.mean():.2f}")
print(f"Worst-case revenue: ${revenues.min():.2f}")Average revenue: $489.22
Worst-case revenue: $325.00
3. Project Management with Sequential Risks
# Project phases must happen in order, later phases only if earlier succeed
n_simulations = 10000; shape = 2; scale = 10; project_times = []
for sim in range(n_simulations):
total_time = 0
for phase in ['design', 'build', 'test', 'deploy']:
# Each phase has uncertain duration
phase_time = np.random.gamma(shape, scale)
total_time += phase_time
if np.random.random() < 0.1:
total_time += phase_time * 0.5 # Rework time
project_times.append(total_time)
project_times = np.array(project_times)
print(f"Average project duration: {project_times.mean():.1f} days")
print(f"90th percentile: {np.percentile(project_times, 90):.1f} days")Average project duration: 84.3 days
90th percentile: 125.2 days
Question: If we can calculate variance analytically, why simulate?
. . .
. . .
Think of our examples as learning the tool on simple problems so you can solve complex ones where Monte Carlo is required!
Even when you CAN use Monte Carlo, sometimes you shouldn’t:
. . .
. . .
Simulation is a tool for managing uncertainty, not creating false precision!
Hour 1:
Lecture
Hour 2:
Practice Notebook
Hours 3-4:
Competition
. . .
Remember: The lecture gives you concepts. The notebook gives you practice. The competition tests your skills!
Your Practice Case: Bean Counter Expansion
TechVenture Investment Competition
. . .
Consider multiple risk metrics and prepare a clear justification!
. . .
Prizes: 10 / 6 / 3 bonus points for top three teams!
Concepts
Skills
np.random for simulation. . .
Monte Carlo doesn’t predict THE future - it shows possible futures! And correlation can amplify or reduce risk!
Forecasting the Future
. . .
Now, short break and then we start coding!