Lecture I - Optimal Stopping

Programming: Everyday Decision-Making Algorithms

Author

Affiliation

Dr. Tobias Vlćek

Kühne Logistics University Hamburg - Winter 2024

About this Course

Teaching Team

About me

Field: Optimizing and simulating complex systems
Languages: of choice: Julia, Python and Rust
Interest: Modelling, Simulations, Machine Learning
Teaching: OR, Algorithms, and Programming
Contact: vlcek@beyondsimulations.com

. . .

Tip

We really appreciate active participation and interaction!

Course Outline

I: Optimal Stopping
II: Explore & Exploit
III: Caching
IV: Scheduling
V: Randomness
VI: Computational Kindness

Participation

Try actively participating in this course
You will find it much (!) easier and more fun
Lecture based on the book Algorithms to live by¹
Material and slides are hosted online: beyondsimulations.github.io/Programming-Everyday-Decisions

Teaching

Lecture: Presentation and discussion of algorithms related to everyday decision-making
Tutorial: Step-by-step assignments to be solved and discussed together in groups
Difficulty: Strongly depends on your background and programming experience

. . .

Tip

No worries, we will help you out if you have any questions!

Passing the Course

Pass/fail course without exams
75% attendance required for passing the course
Hand in the assignments of at least two lectures
Short presentation and discussion at the end
You work together in groups of three students

Handing in Assignments

Each student group submits one solution
Provide us all working notebooks of the lecture
Hand in is due at the beginning of the next lecture
At least 50 % have to be correct to pass
You have to pass at least twice

. . .

Tip

This is just in order to provide you with working solutions after each deadline.

Learning Python

We will mostly not cover Python during the lectures!

. . .

Question: Anybody know why?

. . .

In our experience, the best way to learn is by doing!
Here, we will focus on decision-making algorithms
You will learn Python by doing the tutorials

. . .

Tip

Don’t worry, we will help you out if you have any questions!

Difficulty of the Course

At first it might be a little bit overwhelming
Programming is similar to learning a new language
First, you have to get used to it and learn words
Later, you’ll be able to apply it and see results
Important: Practice, practice, practice!

Goals of the Course

Learn the basics of programming
Learn about algorithmic thinking
Be able to apply methods and concepts
Solve practical problems with algorithms

Tip

We are convinced that this course will be quite interesting and teach you more for your daily life than most other courses!

Why Python?

Origins: Conceived in late 1980s as a teaching and scripting language
Simple Syntax: Python’s syntax is mostly straightforward and very easy to learn
Versatility: Used in web development, data analysis, artificial intelligence, and more
Community Support: A large community of users worldwide and extensive documentation

Help from AI

You are allowed to use AI in the course, we use it as well (e.g., Claude, ChatGPT, LLama3 …)
These tools are great for learning Python!
Can help you a lot to get started with programming

. . .

Warning

But you should not simply use them to replace your learning.

How to learn programming

Our Recommendation

Be present: Attend the lecture and solve the tutorials
Put in some work: Repeat code and try to understand it
Do coding: Run code, play around, modify, and solve

. . .

Tip

Great resources to start are books and small challenges. You can find a list of book recommendations at the end of the lecture. Small challenges to solve can for example be found on Codewars.

Don’t give up!

Programming is problem solving, don’t get frustrated!
Expect to stretch your comfort zone

Setting up Python

The Setup

We will use Jupyter Notebooks for the tutorials
Allow to combine code and text in one document
We will use Visual Studio Code as an IDE

. . .

Tip

IDE = Integrated Development Environment

Install Python

Sources are the Python website or Anaconda
On macOS, Python is often already installed
If not, I recommend Miniconda (via command line)

. . .

Tip

If the installation does not work, let us know!

Install VS Code

Download and install from the website
Built for Windows, Linux and Mac
Install the Python and Jupyter extension
Now you are ready to go!

. . .

Tip

Unsure on how to work with VS Code and notebooks? Take a look at the tutorial from VS Code and/or ask us! We are happy to help you out!

Python on iPads

You can run Python scripts on your iPad
But it is not recommended for the course
However, you could use Juno if you want to
It works locally on your iPad and can run notebooks

. . .

Caution

Not all packages available in Python are available here, thus you might need a computer to solve certain problems. For our course, this should not be a problem.

Your first code

Hello, World!

Task: Create a directory for the course and create a new file called hello_world.py with the following code:

# This is a comment in Python
print("Hello, World!")

Hello, World!

. . .

Run it with the green ‘run’ button or by pressing F5!

. . .

Note

“Hello world” is a classic example to start with. Often used as a test to check if your computer is working properly and that you have installed the necessary software.

Any questions

so far?

Optimal Stopping

What is Optimal Stopping?

Question: Anybody know what optimal stopping is?

Optimal stopping is the problem of:
- choosing the best option
- from a sequence of options
- where the options are revealed one by one

Anybody an

example of

optimal stopping?

Flat Hunting

Hiring applicants

Dating

Searching for a parking spot

“Secretary Problem”

The Secretary Problem

Imagine you’re hiring a secretary
You must interview candidates one by one
Now, you must decide: hire or continue searching
Once you reject a candidate, you cannot go back
How to maximize chance of selecting the best candidate?

. . .

Note

The name is a bit misleading, as the problem is not about hiring a secretary, but about finding the best candidate. It comes from the 1960s and thus a little outdated.

Basic Setup

We have n candidates
We interview them one by one
We must decide to hire or continue searching
Ordinal ranking of candidates

. . .

Question: Anybody know what ordinal ranking is?

Ways to fail

Question: Anybody an idea how we can fail?

. . .

Reject all candidates and never hire - stopping too late
You hire someone too early - stopping too early

Ideas?

Look-and-Leap Strategy

The optimal strategy is to:

Look at the first 37 % of options
Remember the best one seen so far
Choose the next option that’s better than the best seen
Chance of selecting the best candidate is 37 %²
Thus, we can fail with 63 %!

Step-by-step Approximation

With each additional candidate, the chance of getting a new best candidate decreases
- 1 candidate: 100%
- 2 candidates: 50%
- 3 candidates: 33%
- 4 candidates: 25%
- 5 candidates: 20%

. . .

Question: Anybody see a pattern?

Why 37%?

This is based on the geometric distribution
The optimal stopping point is at n/e³
e is the base of the natural logarithm (≈ 2.718)
This comes from maximizing the probability of success

. . .

Computing the number

import math

percentage = 1/math.e
print(f"Percentage of options to look at: {percentage:.3f}%")

candidates = 20
lookout_phase = candidates/math.e
print(f"Look at first {lookout_phase:.3f} candidates")

Percentage of options to look at: 0.368%
Look at first 7.358 candidates

. . .

Note

No worries if you don’t understand the code! We are essentialy just using the formula to calculate the percentage of candidates to look at.

Geometric Distribution

Let’s visualize the success of a simulation with 20 candidates:

Variations

Rejection

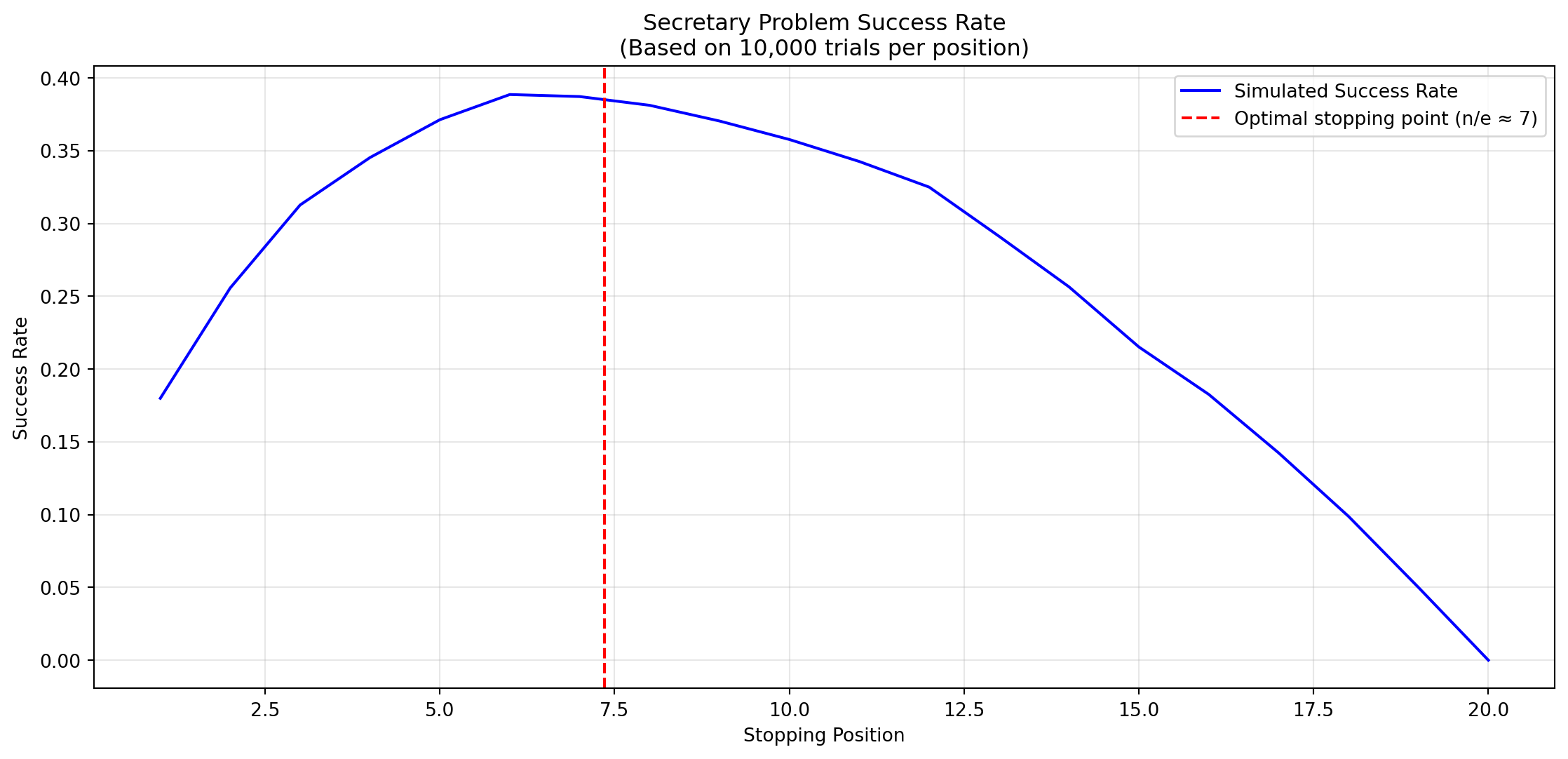
Question: Imagine a dating scenario, where the other person can also reject you. Optimal stopping point?

The optimal stopping point is now lower
Because we can now fail more often
With 50 % chance of rejection, we start leaping at 25 %
Formula: \(q^{\frac{1}{1-q}}\) with \(q\) being the chance of rejection

The role of time

What if we don’t have a fixed number of candidates, but rather a fixed amount of time?

. . .

Imagine we have one year to find a new flat
We want the best flat, but don’t know what a good flat is

. . .

Question: How should we behave?

. . .

Same, but now we decide when to stop searching!

Other versions

Selling a house for the best price (“Threshold Rule”)
Stealing with a success probability (“Burglar’s Problem”)
Finding a parking spot (“Parking Lot Problem”) [^2]

. . .

Note

Side note for drivers: An increase in occupancy from 90 to 95% doubles the search time for all drivers!

Optimal Solution

The Gambler’s Fallacy

Question: Can you imagine a scenario where it would be unwise to use optimal stopping?

. . .

Imagine a game with a 50 % chance of winning
If you win, your payoff is a triple of your bet
If you lose, you have to pay your bet

Questions?

The End

Note

That’s it for todays lecture!
We now have covered a brief introduction into optimal stopping and seen how to set up Python. Now we can start with the tutorials!

Literature

Interesting literature to start

Christian, B., & Griffiths, T. (2016). Algorithms to live by: the computer science of human decisions. First international edition. New York, Henry Holt and Company.⁴
Ferguson, T.S. (1989) ‘Who solved the secretary problem?’, Statistical Science, 4(3). doi:10.1214/ss/1177012493.

Books on Programming

Downey, A. B. (2024). Think Python: How to think like a computer scientist (Third edition). O’Reilly. Here
Elter, S. (2021). Schrödinger programmiert Python: Das etwas andere Fachbuch (1. Auflage). Rheinwerk Verlag.

. . .

Note

Think Python is a great book to start with. It’s available online for free. Schrödinger Programmiert Python is a great alternative for German students, as it is a very playful introduction to programming with lots of examples.

More Literature

For more interesting literature, take a look at the literature list of this course.

Footnotes

Christian, B., & Griffiths, T. (2016). Algorithms to live by: the computer science of human decisions. First international edition. New York, Henry Holt and Company.↩︎
Large number of candidates! With a small number of candidates, we can do even better.↩︎
This is a bit more advanced. We will not go into the details of the math here and focus more on the insights. For more details see Ferguson, T.S. (1989) ‘Who solved the secretary problem?’, Statistical Science, 4(3). doi:10.1214/ss/1177012493.↩︎
The main inspiration for this lecture. Nils and I have read it and discussed it in depth, always wanting to translate it into a course.↩︎