Lecture I - Optimal Stopping

Programming: Everyday Decision-Making Algorithms

Dr. Tobias Vlćek

Kühne Logistics University Hamburg - Winter 2025

Today’s Topic: Optimal Stopping

Topic: Understanding optimal stopping problems and the famous “Secretary Problem”

Why this matters: Optimal stopping is everywhere in life - from hiring decisions to finding apartments to choosing when to sell stocks. Today we’ll learn the mathematical strategy that maximizes your chances of making the best choice.

Learning Objectives

By the end of this lecture, you will be able to:

1. Define optimal stopping problems and identify them in real-world scenarios
2. Apply the 37% rule (look-and-leap strategy) to make better decisions
3. Connect optimal stopping principles to programming logic and algorithmic thinking

Today’s Agenda

1. What is Optimal Stopping? - Definition and real-world examples
2. The Secretary Problem - The classic formulation and solution
3. The 37% Rule - Why it works and how to apply it
4. Variations & Extensions - Rejection, time constraints, other scenarios
5. Connecting to Programming - How this builds our algorithmic mindset

Optimal Stopping

What is Optimal Stopping?

Question: Anybody know what optimal stopping is?

• Optimal stopping is the problem of:
  • choosing the best option
  • from a sequence of options
  • where the options are revealed one by one

Anybody an

example of

optimal stopping?

Flat Hunting

Hiring applicants

Dating

“Secretary Problem”

The Secretary Problem

• Imagine you’re hiring a secretary
• You must interview candidates one by one
• Now, you must decide: hire or continue searching
• Once you reject a candidate, you cannot go back
• How to maximize chance of selecting the best candidate?

The name is a bit misleading, as the problem is not about hiring a secretary, but about finding the best candidate. It comes from the 1960s and thus a little outdated.

Basic Setup

• We have n candidates
• We interview them one by one
• We must decide to hire or continue searching
• Ordinal ranking of candidates

Question: Anybody know what ordinal ranking is?

Ways to fail

Question: Anybody an idea how we can fail?

1. Reject all candidates and never hire - stopping too late
2. You hire someone too early - stopping too early

Ideas?

Look-and-Leap Strategy

The optimal strategy is to:

1. Look at the first 37 % of options
2. Remember the best one seen so far
3. Choose the next option that’s better than the best seen
4. Chance of selecting the best candidate is 37 %¹
5. Thus, we can fail with 63 %!

1. Large number of candidates! With a small number of candidates, we can do even better. . . .

Look-and-Leap Strategy

The mathematically optimal strategy:

1. Look at the first 37% of candidates without hiring anyone
2. Remember the best candidate from this observation phase
3. Leap: Hire the next candidate who is better than the best observed
4. Success rate: 37% chance of selecting the absolute best candidate

This means we fail 63% of the time - but this is the best we can possibly do!

Step-by-step Approximation

Why does the success probability decrease with more candidates?

• 1 candidate: 100% (no choice!)
• 2 candidates: 50%
• 3 candidates: 33%
• 4 candidates: 25%
• 5 candidates: 20%

Question: Do you see the pattern?

Pattern: 1/n - as we have more options, each individual option is less likely to be the best.

Why 37%?

• This is based on the geometric distribution
• The optimal stopping point is at n/e¹
• e is the base of the natural logarithm (≈ 2.718)
• This comes from maximizing the probability of success

1. This is a bit more advanced. We will not go into the details of the math here and focus more on the insights. For more details see Ferguson, T.S. (1989) ‘Who solved the secretary problem?’, Statistical Science, 4(3). doi:10.1214/ss/1177012493.

Computing the number

import math

percentage = 1/math.e
print(f"Percentage of options to look at: {percentage:.3f}%")

candidates = 20
lookout_phase = candidates/math.e
print(f"Look at first {lookout_phase:.3f} candidates")

Percentage of options to look at: 0.368%
Look at first 7.358 candidates

No worries if you don’t understand the code! We are essentialy just using the formula to calculate the percentage of candidates to look at.

Geometric Distribution

Let’s visualize the success of a simulation with 20 candidates:

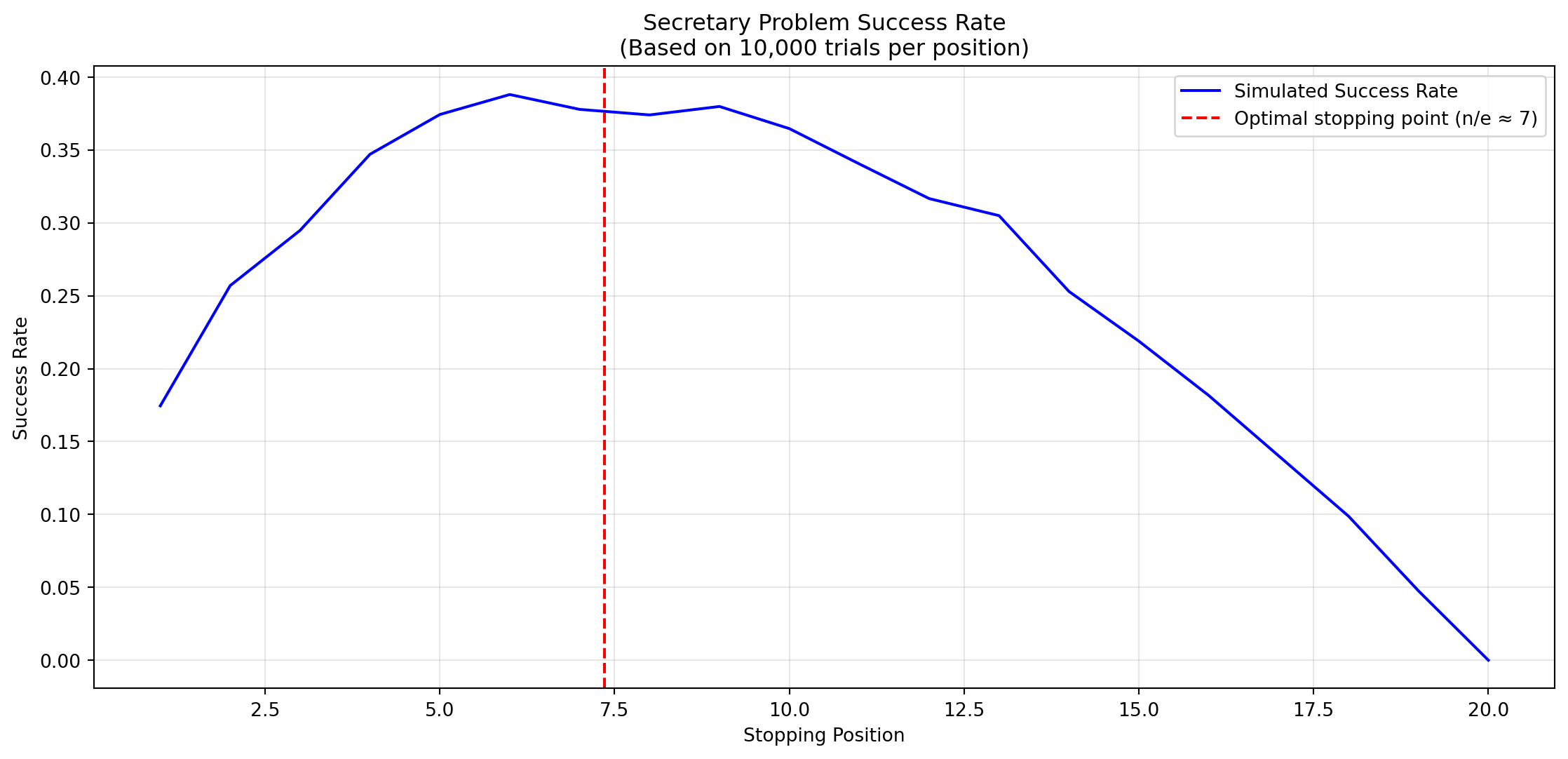
Variations

Rejection

Question: Imagine a dating scenario, where the other person can also reject you. Optimal stopping point?

• The optimal stopping point is now lower
• Because we can now fail more often
• With 50 % chance of rejection, we start leaping at 25 %
• Formula: \(q^{\frac{1}{1-q}}\) with \(q\) being the chance of rejection

Mutual Rejection

Question: What if in dating, the other person can also reject you?

• The optimal stopping point decreases
• We need to account for rejection risk
• With 50% rejection probability: start accepting at 25%
• Formula: \(q^{\frac{1}{1-q}}\) where \(q\) = rejection probability

Life lesson: Higher risk of rejection means we should be less picky!

Time Constraints

What if we don’t have a fixed number of candidates, but a fixed amount of time?

Example: One year to find an apartment

Question: How should we adapt our strategy?

• Same principle applies! Observe for first 37% of available time
• But now we also control the search intensity
• This connects to resource allocation problems in computer science

Other versions

• Selling a house for the best price (“Threshold Rule”)
• Stealing with a success probability (“Burglar’s Problem”)
• Finding a parking spot (“Parking Lot Problem”) [^2]

Side note for drivers: An increase in occupancy from 90 to 95% doubles the search time for all drivers!

Building Your Technical Mindset

Question: How does optimal stopping connect to programming?

1. Algorithmic thinking: Break complex decisions into logical steps
2. Trade-off analysis: Exploration vs. exploitation (fundamental in AI)
3. Mathematical optimization: Using formulas to find best solutions

Key Takeaways

What we learned:

1. Optimal stopping problems are everywhere in life and business
2. The 37% rule provides a mathematically optimal strategy
3. Exploration vs. exploitation is a fundamental trade-off
4. Real-world variations require adapting the basic strategy
5. This thinking builds foundation for algorithmic problem-solving

Any questions

so far?

After the break — Optimal Stopping

• Gentle introduction to Python Programming
• We work in our notebooks on basics and optimal stopping
• How to translate the idea into code and experiments

That’s it for optimal stopping!
Let’s have a short break and then continue with our first Python programming session.

Literature

Interesting literature to start

• Christian, B., & Griffiths, T. (2016). Algorithms to live by: the computer science of human decisions. First international edition. New York, Henry Holt and Company.¹
• Ferguson, T.S. (1989) ‘Who solved the secretary problem?’, Statistical Science, 4(3). doi:10.1214/ss/1177012493.

1. The main inspiration for this lecture. Nils and I have read it and discussed it in depth, always wanting to translate it into a course.

Books on Programming

• Downey, A. B. (2024). Think Python: How to think like a computer scientist (Third edition). O’Reilly. Here
• Elter, S. (2021). Schrödinger programmiert Python: Das etwas andere Fachbuch (1. Auflage). Rheinwerk Verlag.

Think Python is a great book to start with. It’s available online for free. Schrödinger Programmiert Python is a great alternative for German students, as it is a very playful introduction to programming with lots of examples.

More Literature

For more interesting literature, take a look at the literature list of this course.