Session 06-05 - Integration by Parts & Synthesis

Section 06: Integral Calculus

Dr. Nikolai Heinrichs & Dr. Tobias Vlcek

Entry Quiz - 10 Minutes

Quick Review from Session 06-04

Test your understanding of Area Between Curves & Surplus

1. Find the area between \(f(x) = x^2\) and \(g(x) = 2x\) from \(x = 0\) to \(x = 2\).

2. If demand is \(D(q) = 80 - 2q\) and supply is \(S(q) = 20 + q\), find equilibrium \((q^*, p^*)\).

3. Set up (but don’t evaluate) the consumer surplus integral for the market in problem 2.

4. Find \(\int (3x^2 - 4x + 5) \, dx\)

Homework Discussion - 15 Minutes

Your questions from Session 06-04

Focus on area between curves and economic surplus

• Finding intersection points
• Consumer and producer surplus calculations
• Price floor/ceiling effects on surplus
• Deadweight loss interpretation

Today we learn a powerful technique for integrating products of functions and synthesize our integration skills!

Learning Objectives

What You’ll Master Today

• Understand integration by parts as the reverse of the product rule
• Apply the LIATE rule to choose which function to differentiate
• Solve integrals of the form \(\int x \cdot e^x \, dx\)
• Handle repeated application for integrals like \(\int x^2 \cdot e^x \, dx\)
• Compute average value of a function over an interval
• Apply integration to revenue and cost accumulation
• Synthesize techniques from differential and integral calculus

Integration by parts is essential for the Feststellungsprufung!

Part A: The Product Rule in Reverse

Motivation: Why Do We Need This?

Consider this integral:

\[\int x \cdot e^x \, dx\]

Question: Can we use the power rule?

No!

Question: Can we use substitution?

Try \(u = x\) or \(u = e^x\)… Neither works cleanly!

Some products of functions require a special technique.

The Product Rule Revisited

Recall the product rule for derivatives:

\[\frac{d}{dx}[u \cdot v] = u' \cdot v + u \cdot v'\]

Rearranging:

\[u \cdot v' = \frac{d}{dx}[u \cdot v] - u' \cdot v\]

Integrating both sides:

\[\int u \cdot v' \, dx = u \cdot v - \int u' \cdot v \, dx\]

The Integration by Parts Formula

\[\int \underbrace{u(x)}_{\text{choose}} \cdot \underbrace{v'(x) \, dx}_{= \, dv} = u(x) \cdot v(x) - \int \underbrace{v(x)}_{\text{from integrating } dv} \cdot \underbrace{u'(x) \, dx}_{= \, du}\]

This is the same as:

\[\int u \, dv = uv - \int v \, du\]

Strategy: Choose \(u\) and \(dv\) so that \(\int v \, du\) is easier than \(\int u \, dv\)!

What Do \(du\) and \(dv\) Mean?

You already know this notation — from every integral you’ve written!

• When you write \(\int x^2 \, dx\), the \(dx\) tells you what variable you integrate with respect to
• Now, \(du\) works the same way — it just says “with respect to \(u\)”
• The connection between them: if \(u\) is a function of \(x\), we can convert between \(du\) and \(dx\): \(du = u'(x) \, dx\)
• In words: \(du\) is the derivative of \(u\) with respect to \(x\), multiplied by \(dx\)
• The \(dx\) is needed for the remaining integral, don’t worry about it

Question: Do you get the basic idea?

Part B: The LIATE Rule

Choosing \(u\) - The LIATE Rule

How do we choose which function to call \(u\)?

Letter	Function Type	Example
L	Logarithmic	\(\ln(x)\), \(\log(x)\)
I	Inverse trig	\(\arctan(x)\), \(\arcsin(x)\)
A	Algebraic	\(x\), \(x^2\), polynomials
T	Trigonometric	\(\sin(x)\), \(\cos(x)\)
E	Exponential	\(e^x\), \(2^x\)

Choose \(u\) in this order of priority!

Why LIATE Works

The idea: Choose \(u\) to be the function that becomes simpler when differentiated.

• Logarithms (\(\ln x \to \frac{1}{x}\)): Derivatives are simpler
• Algebraic (\(x^n \to nx^{n-1}\)): Powers decrease
• Exponentials (\(e^x \to e^x\)): Don’t simplify - put in \(dv\)!

The LIATE rule is a guideline, not a strict rule. Sometimes you need to experiment!

Part C: Basic Examples

Example 1: \(\int x \cdot e^x \, dx\)

Step 1: Identify \(u\) and \(dv\) using LIATE: choose \(u = x\) (A comes before E)

Step 2: Set up the parts

We choose:	We compute:
\(u = x\)	\(du = 1 \cdot dx = dx\) (differentiate \(u\), attach \(dx\))
\(dv = e^x \, dx\)	\(v = \int e^x \, dx = e^x\) (integrate \(dv\) to get \(v\))

Step 3: Apply the formula \(\int u \, dv = uv - \int v \, du\)

\[\int \underbrace{x}_{u} \cdot \underbrace{e^x \, dx}_{dv} = \underbrace{x}_{u} \cdot \underbrace{e^x}_{v} - \int \underbrace{e^x}_{v} \, \underbrace{dx}_{du}\]

Example 1: Solution

\[\int x \cdot e^x \, dx = x \cdot e^x - \int e^x \, dx\]

\[= x \cdot e^x - e^x + C\]

\[= e^x(x - 1) + C\]

Verification: Differentiate to check: \[\frac{d}{dx}[e^x(x-1)] = e^x(x-1) + e^x \cdot 1 = e^x \cdot x - e^x + e^x = x \cdot e^x \quad \checkmark\]

Example 2: \(\int (x+1) \cdot e^x \, dx\)

This is a common exam problem!

Step 1: Choose \(u = x + 1\) (algebraic), \(dv = e^x \, dx\)

We choose:	We compute:
\(u = x + 1\)	\(du = 1 \cdot dx = dx\) (differentiate \(u\), attach \(dx\))
\(dv = e^x \, dx\)	\(v = \int e^x \, dx = e^x\) (integrate \(dv\) to get \(v\))

Step 2: Apply the formula

\[\int (x+1) \cdot e^x \, dx = (x+1) \cdot e^x - \int e^x \, dx\]

\[= (x+1) \cdot e^x - e^x + C = e^x(x + 1 - 1) + C = x \cdot e^x + C\]

Example 3: \(\int x \cdot \ln(x) \, dx\)

Step 1: Identify using LIATE: choose \(u = \ln(x)\) (L comes first!)

Step 2: Set up the parts

We choose:	We compute:
\(u = \ln(x)\)	\(du = \frac{1}{x} \cdot dx\) (differentiate \(u\), attach \(dx\))
\(dv = x \, dx\)	\(v = \int x \, dx = \frac{x^2}{2}\) (integrate \(dv\) to get \(v\))

Step 3: Apply the formula

\[\int x \cdot \ln(x) \, dx = \ln(x) \cdot \frac{x^2}{2} - \int \frac{x^2}{2} \cdot \frac{1}{x} \, dx\]

Example 3: Solution

\[\int x \cdot \ln(x) \, dx = \frac{x^2 \ln(x)}{2} - \int \frac{x}{2} \, dx\]

\[= \frac{x^2 \ln(x)}{2} - \frac{x^2}{4} + C\]

\[= \frac{x^2}{4}\left(2\ln(x) - 1\right) + C\]

Notice how choosing \(u = \ln(x)\) simplified the integral because \(\frac{1}{x} \cdot x^2 = x\) (simpler than before).

Break - 10 Minutes

Part D: Repeated Integration by Parts

When One Application Isn’t Enough

Consider: \(\int x^2 \cdot e^x \, dx\)

First application: \(u = x^2\), \(dv = e^x \, dx\)

We choose:	We compute:
\(u = x^2\)	\(du = 2x \cdot dx\) (differentiate \(u\), attach \(dx\))
\(dv = e^x \, dx\)	\(v = \int e^x \, dx = e^x\) (integrate \(dv\) to get \(v\))

\[\int x^2 \cdot e^x \, dx = x^2 \cdot e^x - \int 2x \cdot e^x \, dx\]

Problem: We still have \(\int x \cdot e^x \, dx\) - another integration by parts problem!

Repeated Application

Second application: For \(\int x \cdot e^x \, dx\), let \(u = x\), \(dv = e^x \, dx\)

\[\int x \cdot e^x \, dx = x \cdot e^x - e^x\]

Substituting back:

\[\int x^2 \cdot e^x \, dx = x^2 \cdot e^x - 2(x \cdot e^x - e^x) + C\]

\[= x^2 \cdot e^x - 2x \cdot e^x + 2e^x + C= e^x(x^2 - 2x + 2) + C\]

Exam Example: \(\int x^2 \cdot e^{-x} \, dx\)

This exact type appeared on the exam!

First application: \(u = x^2\), \(dv = e^{-x} \, dx\), so \(v = -e^{-x}\)

\[\int x^2 \cdot e^{-x} \, dx = -x^2 \cdot e^{-x} - \int -2x \cdot e^{-x} \, dx\]

\[= -x^2 \cdot e^{-x} + 2\int x \cdot e^{-x} \, dx\]

Second application: \(u = x\), \(dv = e^{-x} \, dx\), so \(v = -e^{-x}\)

\[\int x \cdot e^{-x} \, dx = -x \cdot e^{-x} + \int e^{-x} \, dx = -x \cdot e^{-x} - e^{-x}\]

Exam Example: Final Answer

Substituting back:

\[\int x^2 \cdot e^{-x} \, dx = -x^2 \cdot e^{-x} + 2(-x \cdot e^{-x} - e^{-x}) + C\]

\[= -x^2 \cdot e^{-x} - 2x \cdot e^{-x} - 2e^{-x} + C\]

\[= -e^{-x}(x^2 + 2x + 2) + C\]

Verification is important! Differentiate your answer if you have the time: \[\frac{d}{dx}[-e^{-x}(x^2+2x+2)] = e^{-x}(x^2+2x+2-2x-2) = x^2 e^{-x}\]

Part E: Definite Integrals by Parts

Definite Integrals with Bounds

For definite integrals:

\[\int_a^b u \, dv = [uv]_a^b - \int_a^b v \, du\]

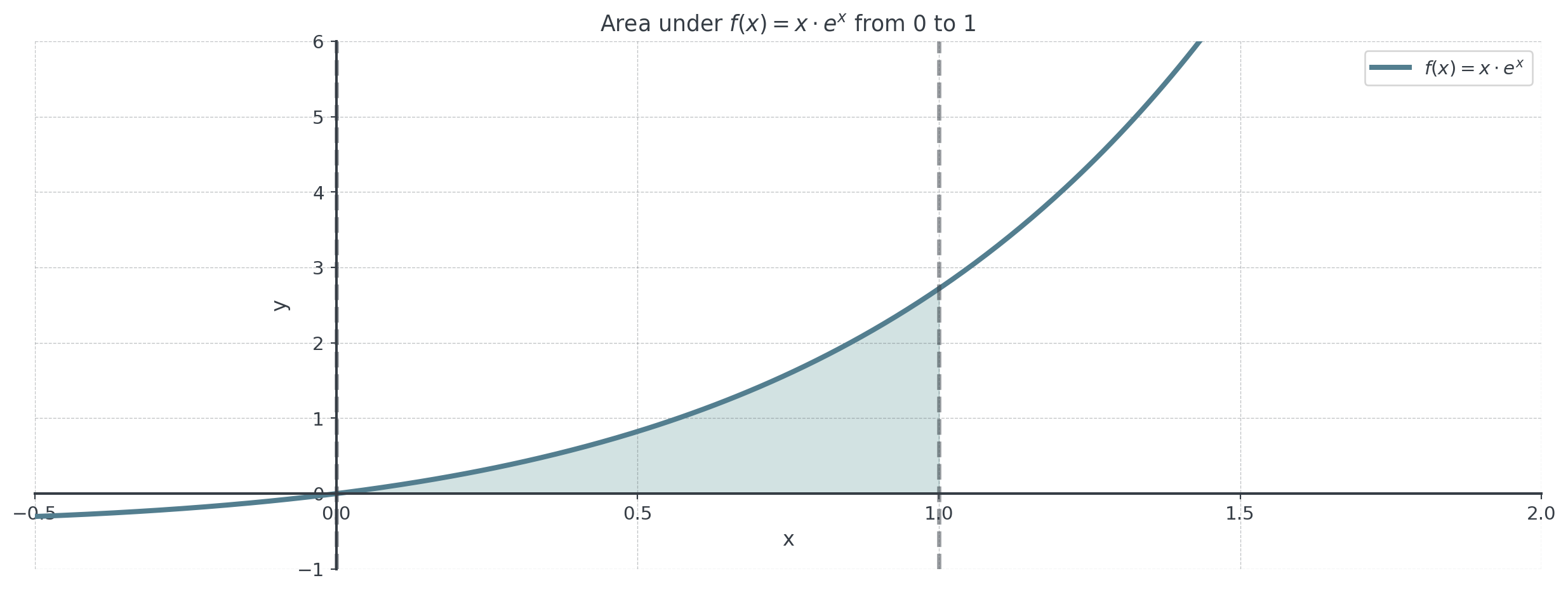
Example: \(\int_0^1 x \cdot e^x \, dx\), we found \(\int x \cdot e^x \, dx = e^x(x - 1) + C\)

\[\int_0^1 x \cdot e^x \, dx = [e^x(x-1)]_0^1 = e^1(1-1) - e^0(0-1)\]

\[= 0 - (-1) = 1\]

Definite Integral Example with Graph

Essentially, we use integration by parts and then compute the definite integral as learned.

Guided Practice - 20 Minutes

Practice Set A: Single Application

Work individually for 5 minutes

1. \(\int 3x \cdot e^x \, dx\)
2. \(\int (2x + 1) \cdot e^x \, dx\)
3. \(\int x \cdot e^{-x} \, dx\)
4. \(\int x^2 \cdot \ln(x) \, dx\)

Practice Set B: Repeated Application

Work individually for 7 minutes

1. \(\int x^2 \cdot e^{2x} \, dx\)
2. \(\int (x^2 + x) \cdot e^x \, dx\)
3. \(\int_0^2 x \cdot e^x \, dx\) (evaluate with bounds)

Coffee Break - 15 Minutes

Part F: Average Value of a Function

The Average Value Formula

Key idea: What is the “average height” of a function over an interval?

\[f_{avg} = \frac{1}{b-a} \int_a^b f(x) \, dx\]

The Average Visualized

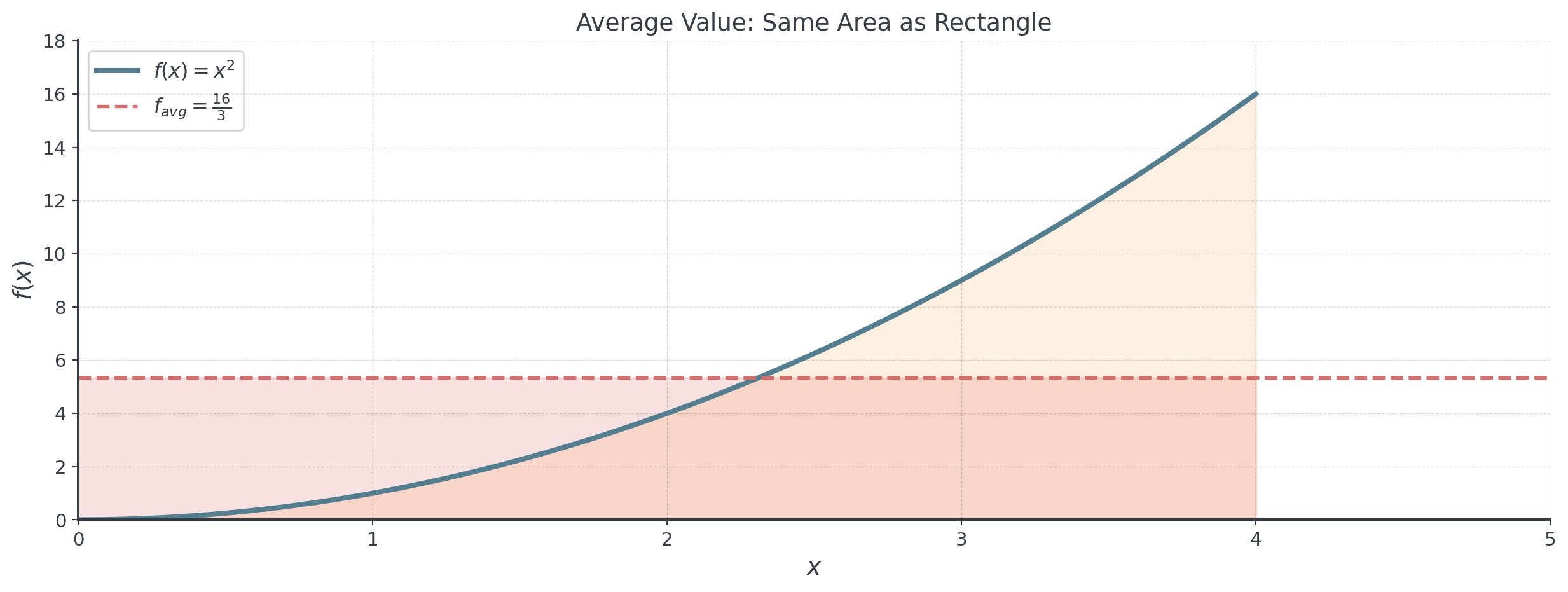
Makes sense, doesn’t it?

Example: Average Value

Find the average value of \(f(x) = x^2\) on \([0, 4]\)

\[f_{avg} = \frac{1}{4-0} \int_0^4 x^2 \, dx\]

\[= \frac{1}{4} \left[\frac{x^3}{3}\right]_0^4\]

\[= \frac{1}{4} \cdot \frac{64}{3} = \frac{16}{3} \approx 5.33\]

The area under \(f(x)\) equals the area of a rectangle with height \(f_{avg}\) and width \((b-a)\).

Part G: Revenue and Cost Accumulation

Total Revenue from Marginal Revenue

Key relationship: If \(MR(x)\) is the marginal revenue, then total revenue from selling \(a\) to \(b\) units is:

\[\text{Revenue}_{a \to b} = \int_a^b MR(x) \, dx\]

Example: \(MR(x) = 100 - 2x\), revenue from selling units 10 to 30:

\[\int_{10}^{30} (100 - 2x) \, dx = [100x - x^2]_{10}^{30}\]

\[= (3000 - 900) - (1000 - 100) = 2100 - 900 = 1200 \text{ EUR}\]

Profit Accumulation Over Time

Scenario: Profit rate \(P'(t) = 8t - t^2\) thousand EUR per month (\(t\))

Find total profit from month 2 to month 6.

\[P_{2 \to 6} = \int_2^6 (8t - t^2) \, dt = \left[4t^2 - \frac{t^3}{3}\right]_2^6\]

\[= \left(144 - 72\right) - \left(16 - \frac{8}{3}\right)\]

\[= 72 - \frac{40}{3} = \frac{216 - 40}{3} = \frac{176}{3} \approx 58.67 \text{ thousand EUR}\]

Collaborative Problem-Solving - 25 Minutes

Practice Set C: Synthesis

Work with a partner for 10 minutes

1. Find the average value of \(f(x) = 2x + 1\) on \([0, 4]\)

2. A company’s marginal profit is \(P'(x) = 80 - 4x\) EUR/unit.

   1. Find the production level \(x^*\) that maximizes profit.
   2. Calculate the total profit from \(x = 5\) to \(x = 15\).

3. A machine’s production rate is \(P(t) = 100e^{-0.1t}\) units/hour. Find the average production rate over the first 10 hours.

Challenge: Present Value Analysis

Scenario: A company expects future profits that decay over time. The profit rate is the follwoing where \(t\) is years and profit is in thousands of euros.

\[P'(t) = (100 + 20t) \cdot e^{-0.05t}\]

1. Find the antiderivative of the profit rate using integration by parts

2. Calculate the total profit from year 0 to year 10

3. At what rate is profit changing at \(t = 5\)?

4. Interpret the results for a business decision

Wrap-Up & Key Takeaways

What We’ve Learned in Section 06

1. Antiderivatives reverse differentiation: \(F'(x) = f(x)\)
2. Definite integrals compute net accumulated change
3. Area under curves using \(\int_a^b f(x) \, dx\)
4. Area between curves using \(\int_a^b [f(x) - g(x)] \, dx\)
5. Consumer Surplus: \(CS = \int_0^{q^*} [D(q) - p^*] \, dq\)
6. Producer Surplus: \(PS = \int_0^{q^*} [p^* - S(q)] \, dq\)
7. Integration by Parts: \(\int u \, dv = uv - \int v \, du\)
8. Average Value: \(f_{avg} = \frac{1}{b-a} \int_a^b f(x) \, dx\)

Essential Formulas Summary

Concept	Formula
Antiderivative	\(\int x^n \, dx = \frac{x^{n+1}}{n+1} + C\)
FTC	\(\int_a^b f(x) \, dx = F(b) - F(a)\)
Area Between	\(\int_a^b [f(x) - g(x)] \, dx\)
Consumer Surplus	\(\int_0^{q^*} [D(q) - p^*] \, dq\)
Producer Surplus	\(\int_0^{q^*} [p^* - S(q)] \, dq\)
Integration by Parts	\(\int u \, dv = uv - \int v \, du\)
Average Value	\(\frac{1}{b-a} \int_a^b f(x) \, dx\)

Final Assessment - 5 Minutes

Quick Check

Work individually

1. Find \(\int (x + 2) \cdot e^x \, dx\)

2. Find the average value of \(f(x) = x^2\) on \([1, 3]\).

3. Why does LIATE put logarithms before algebraic functions?

4. What does consumer surplus measure economically?

Next Session Preview

Session 06-06: Mock Exam

Comprehensive Assessment

• Full mock exam covering differential and integral calculus
• 180 minutes working time with problems covering:
  • Graphical differentiation and integration
  • Function analysis with calculus
  • Area calculations
  • Economic applications
  • Integration by parts

Complete tasks and review all integration techniques!