Session 05-03 - Differentiation Rules & Tangent Lines

Section 05: Differential Calculus

Dr. Nikolai Heinrichs & Dr. Tobias Vlćek

Entry Quiz - 10 Minutes

Quick Review from Session 05-02

Test your understanding of derivatives as rate of change

  1. Using the limit definition, find \(f'(x)\) if \(f(x) = 3x^2\).

  2. What is the derivative of \(g(x) = 5x\) using the limit definition?

  3. For the cost function \(C(x) = 100 + 20x\), what is \(C'(x)\) and what does it mean in business terms?

  4. If the slope of the tangent line to \(f(x)\) at \(x = 2\) is 5, what is \(f'(2)\)?

Homework Discussion - 15 Minutes

Your questions from Session 05-02

What questions do you have regarding the tasks?

Learning Objectives

What You’ll Master Today

  • Master differentiation rules to avoid tedious limit calculations
  • Apply product and quotient rules correctly and efficiently
  • Find equations of tangent lines at specific points on curves
  • Use linear approximation for estimation in business contexts
  • Choose optimal strategies for differentiating complex functions

Key Insight

Today we develop shortcuts that make differentiation fast and efficient, no more slow limit algebra!

Part A: Power, Constant, and Sum Rules

Why We Need Rules

The Problem: Computing derivatives from limit definition is tedious!

  • For \(f(x) = x^{10}\), the binomial expansion has 11 terms
  • For \(f(x) = (x^2 + 3x + 1)^{50}\), it’s essentially impossible
  • We need shortcuts that give the same answer faster

The Solution: Differentiation rules, formulas that work every time!

The Power Rule

Power Rule: \[\frac{d}{dx}[x^n] = nx^{n-1}\]

where \(n\) is any real number.

Examples:

  • \(\frac{d}{dx}[x^5] = 5x^4\)
  • \(\frac{d}{dx}[\sqrt{x}] = \frac{d}{dx}[x^{1/2}] = \frac{1}{2}x^{-1/2} = \frac{1}{2\sqrt{x}}\)
  • \(\frac{d}{dx}\left[\frac{1}{x^3}\right] = \frac{d}{dx}[x^{-3}] = -3x^{-4} = -\frac{3}{x^4}\)

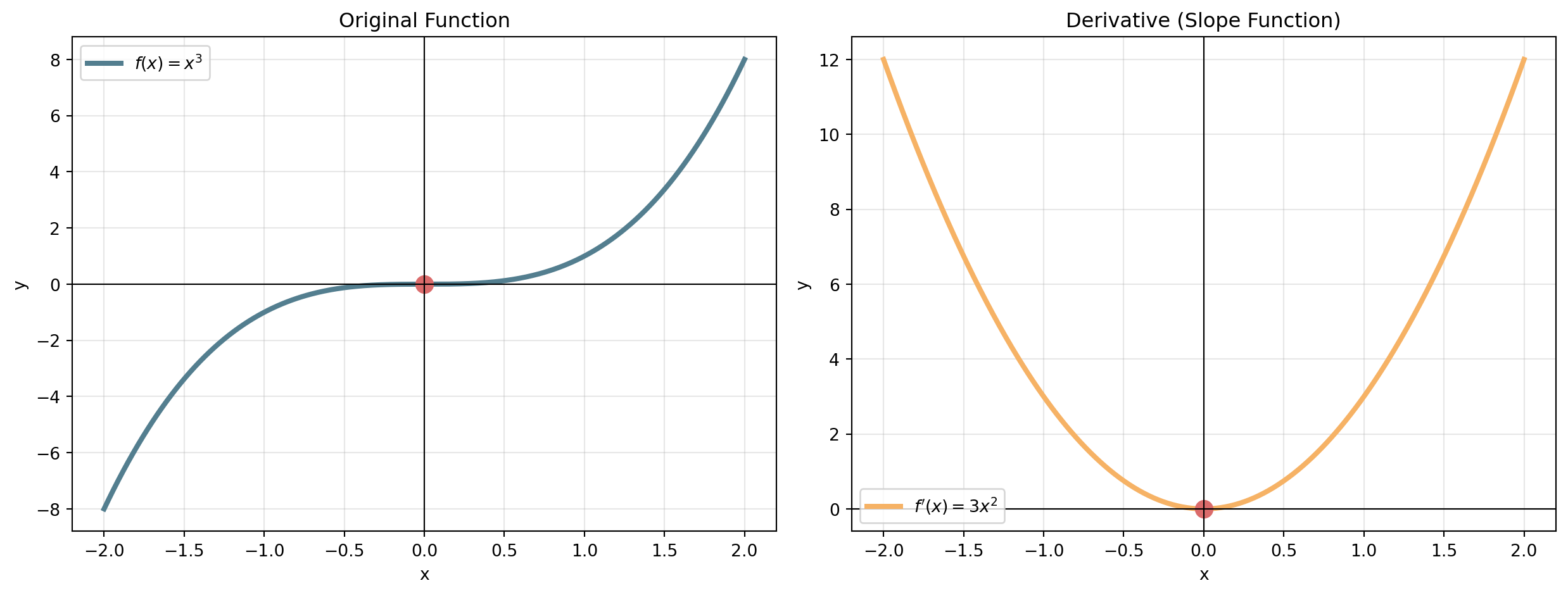
Visualizing the Power Rule

  • Where \(f(x) = x^3\) is increasing, \(f'(x) = 3x^2 > 0\)
  • At \(x = 0\), \(f\) has a horizontal tangent, so \(f'(0) = 0\)

Constant Rules

Constant Rule: \[\frac{d}{dx}[c] = 0\]

where \(c\) is any constant.

  • Constants don’t change, so their rate of change is zero!
  • Examples: \(\frac{d}{dx}[7] = 0\), \(\frac{d}{dx}[\pi] = 0\), \(\frac{d}{dx}[-42] = 0\)

This is one is very easy, right?

Constant Multiple Rules

Constant Multiple Rule: \[\frac{d}{dx}[c \cdot f(x)] = c \cdot f'(x)\]

  • Pull constants out front!
  • Examples: \(\frac{d}{dx}[5x^3] = 5(3x^2) = 15x^2\)
  • \(\frac{d}{dx}\left[\frac{3}{x^2}\right] = 3 \cdot \frac{d}{dx}[x^{-2}] = 3(-2x^{-3}) = -\frac{6}{x^3}\)

Do you get the idea? Essentially, we just keep the constant if multiplied with a variable.

The Sum Rule

Sum Rule: \[\frac{d}{dx}[f(x) + g(x)] = f'(x) + g'(x)\]

Also works for differences: \(\frac{d}{dx}[f(x) - g(x)] = f'(x) - g'(x)\)

Differentiate term by term!

  • \(\frac{d}{dx}[x^3 + x^2] = 3x^2 + 2x\)
  • \(\frac{d}{dx}[4x^5 - 2x^3 + 7] = 20x^4 - 6x^2 + 0 = 20x^4 - 6x^2\)
  • \(\frac{d}{dx}\left[\sqrt{x} + \frac{1}{x}\right] = \frac{1}{2\sqrt{x}} - \frac{1}{x^2}\)

Combining the Basic Rules

Example: Differentiate \(f(x) = 3x^4 - 2x^2 + 5x - 7\)

\[f'(x) = 3(4x^3) - 2(2x) + 5(1) - 0 = 12x^3 - 4x + 5\]

Example: Differentiate \(g(x) = \frac{2}{x^3} + 4\sqrt{x} - 3\)

\[g(x) = 2x^{-3} + 4x^{1/2} - 3\]

\[g'(x) = 2(-3x^{-4}) + 4\left(\frac{1}{2}x^{-1/2}\right) - 0 = -\frac{6}{x^4} + \frac{2}{\sqrt{x}}\]

Part B: The Product Rule

The Product Rule

Product Rule: \[\frac{d}{dx}[u(x) \cdot v(x)] = u'(x) \cdot v(x) + u(x) \cdot v'(x)\]

“First times derivative of second, plus second times derivative of first”

Common Product Rule Mistakes

  1. Wrong: \((fg)' = f' \cdot g'\) (The product of derivatives)
  2. Wrong: Forgetting one of the two terms
  3. Right: \((fg)' = f'g + fg'\) (Both terms, both factors in each)

If in doubt, check by expanding first when possible!

Product Rule Example

Example: Differentiate \(f(x) = x^3(2x + 5)\)

Let \(u = x^3\) and \(v = 2x + 5\)

  • \(u' = 3x^2\)
  • \(v' = 2\)
  • \(f'(x) = (3x^2)(2x + 5) + (x^3)(2)\)
  • \(f'(x) = 6x^3 + 15x^2 + 2x^3 = 8x^3 + 15x^2\)

Check by expanding first

  • \(f(x) = 2x^4 + 5x^3 \Rightarrow f'(x) = 8x^3 + 15x^3 = 8x^3 + 15x^2\)

When to Use Product Rule?

Some rules of thumb to remember:

  • Use it when: Expanding would be tedious: \((x^2 + 1)^{10}(x^3 - 2)^5\)
  • Skip it when: Easy to expand: \(x(x + 1) = x^2 + x\)
  • Remember: One factor is constant? Use constant multiple rule instead!

Let’s practice these rules!

Quick Practice - 10 Minutes

Individual Exercise

Work individually for 10 minutes

Differentiate the following:

  1. \(f(x) = x^7 - 3x^4 + 2x - 5\)

  2. \(g(x) = 4\sqrt{x} + \frac{2}{x} - 3\)

  3. \(h(x) = (x^2 + 1)(3x - 2)\)

  4. \(k(x) = x^4(x^2 - 5x + 1)\)

Break - 10 Minutes

Part C: The Quotient Rule

Differentiating Quotients

The Quotient Rule: \[\frac{d}{dx}\left[\frac{u(x)}{v(x)}\right] = \frac{u'(x) \cdot v(x) - u(x) \cdot v'(x)}{[v(x)]^2}\]

“Low d-High minus High d-Low, over Low squared”

Common Mistake

\(\left(\frac{f}{g}\right)' \neq \frac{f'}{g'}\) Always use the full quotient rule formula!

Quotient Rule Example

Example: Differentiate \(f(x) = \frac{x^2 + 1}{x - 3}\)

Let \(u = x^2 + 1\) and \(v = x - 3\)

  • \(u' = 2x\)
  • \(v' = 1\)
  • \(f'(x) = \frac{(2x)(x - 3) - (x^2 + 1)(1)}{(x - 3)^2}\)
  • \(= \frac{2x^2 - 6x - x^2 - 1}{(x - 3)^2}\)
  • \(= \frac{x^2 - 6x - 1}{(x - 3)^2}\)

More Examples

Example: Differentiate \(g(x) = \frac{2x}{x + 1}\)

\[g'(x) = \frac{2(x + 1) - 2x(1)}{(x + 1)^2} = \frac{2x + 2 - 2x}{(x + 1)^2} = \frac{2}{(x + 1)^2}\]

Example: Differentiate \(h(x) = \frac{x^2 - 4}{x^2 + 4}\)

\[h'(x) = \frac{2x(x^2 + 4) - (x^2 - 4)(2x)}{(x^2 + 4)^2}\] \[= \frac{2x^3 + 8x - 2x^3 + 8x}{(x^2 + 4)^2} = \frac{16x}{(x^2 + 4)^2}\]

Part D: Tangent Lines & Linear Approximation

Finding Tangent Lines (TL)

TL to \(y = f(x)\) at \(x = a\) has slope \(f'(a)\) and passes \((a, f(a))\).

Equation of Tangent Line: \[y - f(a) = f'(a)(x - a)\]

or in slope-intercept form: \[y = f(a) + f'(a)(x - a)\]

  1. Find the point: Compute \(f(a)\)
  2. Find the slope: Compute \(f'(a)\)
  3. Write the equation using point-slope form

Tangent Line Example

Example: Find the tangent line to \(f(x) = x^2 - 3x + 1\) at \(x = 2\).

Step 1: Find the point

  • \(f(2) = 4 - 6 + 1 = -1\), Point: \((2, -1)\)

Step 2: Find the slope

  • \(f'(x) = 2x - 3\), \(f'(2) = 4 - 3 = 1\)

Step 3: Equation

  • \(y - (-1) = 1(x - 2)\), \(y = x - 3\)

Visualizing the Tangent Line

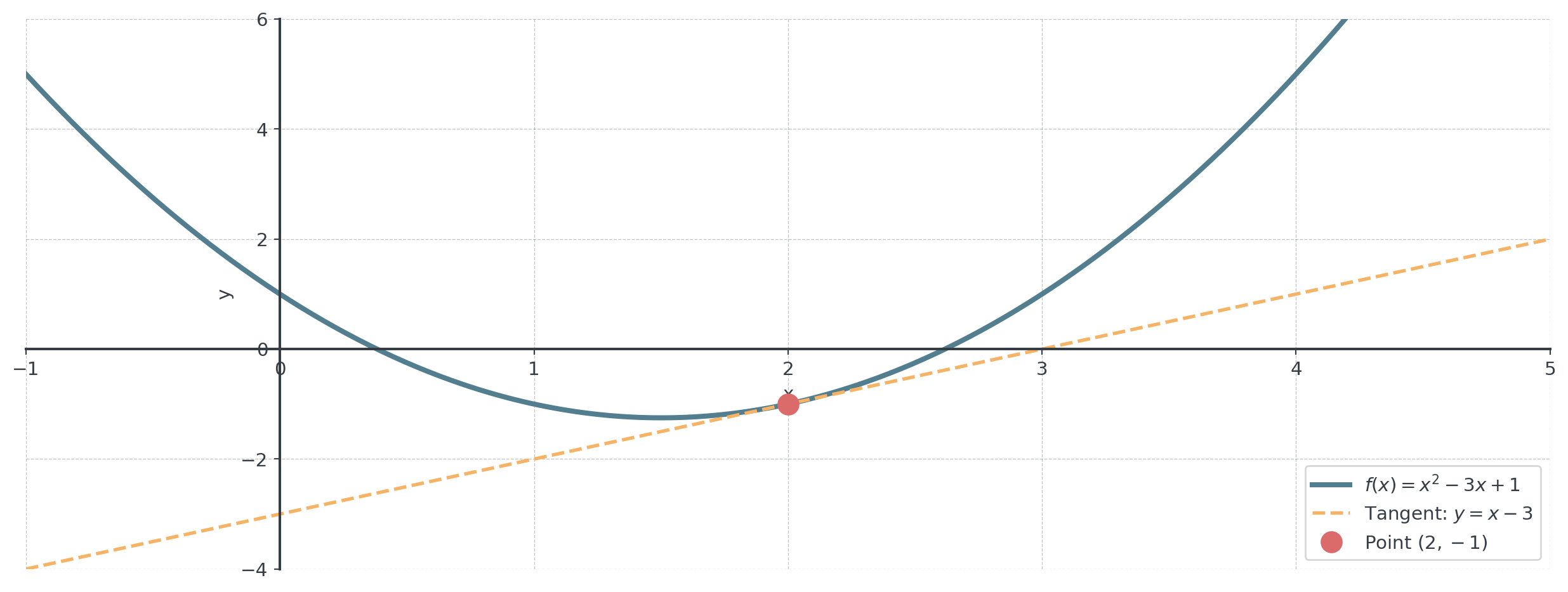
Not too complicated, right?

Linear Approximation

Linear Approximation: For \(x\) near \(a\): \[f(x) \approx f(a) + f'(a)(x - a)\]

This uses the tangent line to estimate function values!

Business Application

When \(x\) changes slightly from \(a\), the change in \(f(x)\) is approximately: \[\Delta f \approx f'(a) \cdot \Delta x\]

This is the basis of sensitivity analysis in economics!

Approximation Example

Example: A company’s profit is

\[P(x) = -0.1x^2 + 5x - 10\]

(in thousands €) where \(x\) is production in thousands of units.

  • Currently producing \(x = 20\) thousand units
  • Estimate profit if production increases to 21 thousand.

Question: How would you estimate the profit change?

Guided Practice - 25 Minutes

Practice Set A: Quotient Rule

Work in pairs for 15 minutes

Differentiate the following using the quotient rule:

  1. \(f(x) = \frac{x^2 + 3}{x - 1}\)

  2. \(g(x) = \frac{2x - 5}{3x + 2}\)

  3. \(h(x) = \frac{x^3}{x^2 + 1}\)

Practice Set B: Tangent Lines

Continue working in pairs for 10 minutes

A company’s revenue function is \(R(x) = 50x - 0.5x^2\) where \(x\) is the number of units sold (in hundreds).

  1. Find \(R'(x)\) and interpret its meaning.

  2. Find the equation of the tangent line to \(R(x)\) at \(x = 30\).

  3. Use the tangent line to estimate \(R(31)\).

  4. Compare your estimate to the actual value \(R(31)\).

Coffee Break - 15 Minutes

Business Applications

Marginal Analysis with Differentiation

A manufacturer has:

  • Cost: \(C(x) = 1000 + 50x + 0.5x^2\)
  • Revenue: \(R(x) = 200x - 0.5x^2\)

where \(x\) is production in hundreds of units.

Marginal functions:

  • \(MC(x) = C'(x) = 50 + x\)
  • \(MR(x) = R'(x) = 200 - x\)
  • Profit: \(P(x) = R(x) - C(x) = -x^2 + 150x - 1000\)
  • \(MP(x) = P'(x) = -2x + 150\)

Profit Maximization

Question: At what production level is profit maximized?

Set \(MR = MC\): \[200 - x = 50 + x \rightarrow 150 = 2x\] \[x = 75 \text{ (hundreds of units)}\]

Optimal profit: \[P(75) = -(75)^2 + 150(75) - 1000 = 4625 \text{ hundred €}\]

The maximum profit is €462,500 at 7,500 units.

Visualizing Marginal Analysis

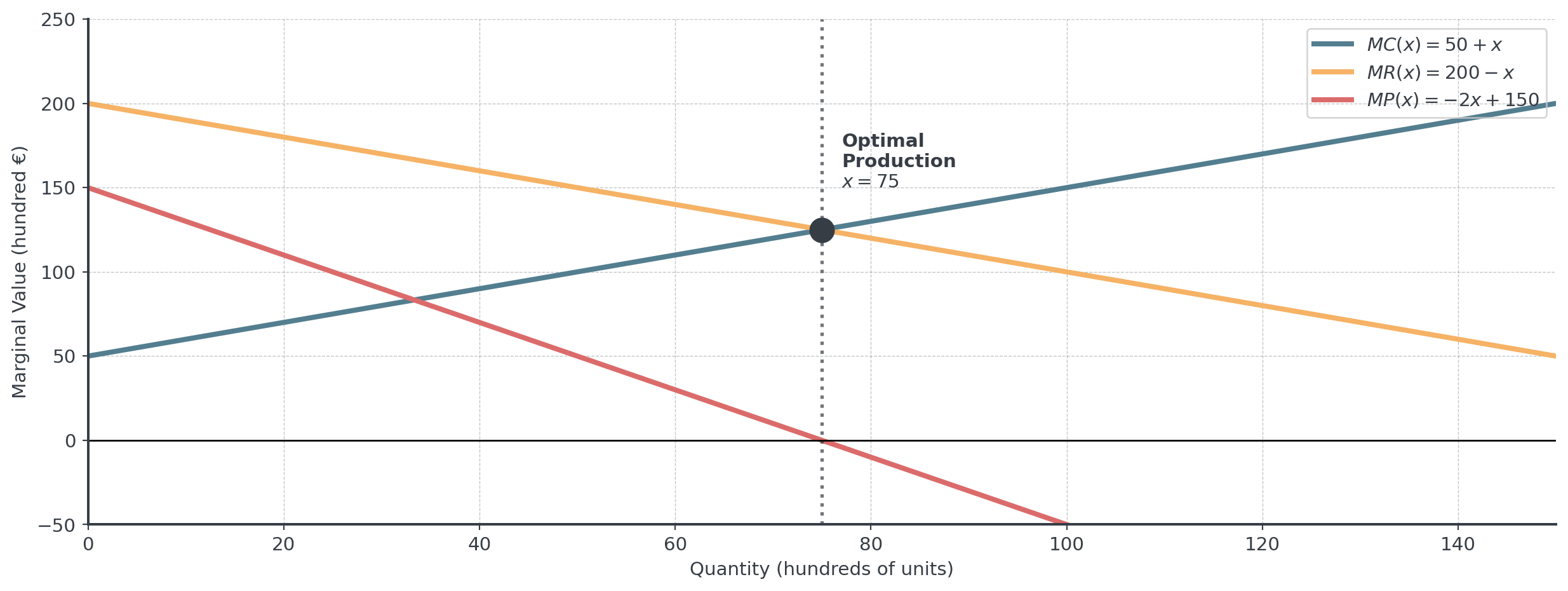
  • For \(x < 75\): \(MR > MC\), so increasing production increases profit
  • For \(x > 75\): \(MR < MC\), so increasing production decreases profit

Sensitivity Analysis Example

A software company’s monthly user base \(U(t)\) (in thousands) follows: \[U(t) = 10 + 2t + 0.1t^2\] where \(t\) is months since launch.

Revenue per user decreases with scale: \(r(u) = 20 - 0.05u\)

Total revenue: \(R(t) = U(t) \cdot r(U(t))\)

Question: How sensitive is revenue to time at \(t = 10\) months?

Collaborative Problem-Solving

Challenge: Production Optimization

You’re consulting for a manufacturing company. They produce specialty components with:

  • Total Cost: \(C(q) = 2000 + 40q + 0.2q^2\) (in €)
  • Market Price: \(p = 100 - 0.1q\) (price decreases as quantity increases)
  • Revenue: \(R(q) = q \cdot p = q(100 - 0.1q) = 100q - 0.1q^2\)

where \(q\) is quantity in units.

Tasks

Work in groups of 3-4

  1. Find marginal cost \(MC(q)\) and marginal revenue \(MR(q)\) functions.

  2. Determine profit-maximizing production level.

  3. Calculate the actual maximum profit at this level.

  4. Find the tangent line to the profit function at the optimal point.

  5. The company is considering increasing production by 10 from the optimum. Use linear approximation to estimate the change in profit.

  6. Discuss: Why is \(MR = MC\) the condition for profit maximization? What happens if \(MR > MC\) or \(MR < MC\)?

Think-Pair-Share

Discussion Question

Think individually, then we discuss

Question: Consider two functions:

  • Function A: \(f(x) = (x + 1)(x + 2)\)
  • Function B: \(g(x) = x^2 + 3x + 2\)

When finding derivatives:

  1. Are these functions the same?
  2. Would you use different differentiation strategies?
  3. Which approach is more efficient and why?

Wrap-Up & Key Takeaways

Today’s Essential Rules

We covered quite some rules today:

Rule Formula When to Use
Power Rule \(\frac{d}{dx}[x^n] = nx^{n-1}\) Any power of \(x\)
Constant Rule \(\frac{d}{dx}[c] = 0\) Constants
Sum Rule \((f + g)' = f' + g'\) Sums/differences
Constant Multiple \((cf)' = cf'\) Constants times functions
Product Rule \((uv)' = u'v + uv'\) Products of functions
Quotient Rule \(\left(\frac{u}{v}\right)' = \frac{u'v - uv'}{v^2}\) Quotients of functions

Rule Selection Strategy

Before differentiating, ask:

  1. Can I simplify first? → Expand products, simplify fractions
  2. Is it a sum/difference? → Differentiate term by term
  3. Is it a simple power? → Use power rule
  4. Is it a product that can’t simplify? → Product rule
  5. Is it a quotient? → Quotient rule (or rewrite as negative power)
  • Marginal analysis: Derivatives give marginal cost, revenue, profit
  • Optimization: Set \(MR = MC\) to maximize profit
  • Sensitivity analysis: \(f'(a)\) shows how sensitive output is to input changes

Final Assessment

Quick Check

Work individually then we discuss

  1. Find \(\frac{d}{dx}[x^4 - 2x^2 + 7]\).

  2. Differentiate \(f(x) = x^2(3x + 1)\) using the product rule.

  3. What is the equation of the tangent line to \(f(x) = x^3\) at \(x = 1\)?

  4. True or False: The derivative of a quotient equals the quotient of derivatives.

Next Session Preview

Session 05-04

Chain Rule & Implicit Differentiation

  • The Chain Rule: How to differentiate composite functions
  • Combining techniques: Chain rule with product and quotient rules
  • Implicit differentiation: Finding \(\frac{dy}{dx}\) when you can’t solve for \(y\)
  • Related rates: How rates of change in different quantities are connected
  • Business: Nested economic functions, inflation adjustments

Complete Tasks 05-03!