Session 03-05 - Composition, Inverses & Advanced Graphing

Section 03: Functions as Business Models

Dr. Nikolai Heinrichs & Dr. Tobias Vlćek

Entry Quiz - 10 Minutes

Review from Session 03-04

Work individually, then exchange with your neighbor for peer review

Given \(f(x) = 2x^2 - 8x + 6\):
1. Write the function shifted left 3 units
2. Write the function stretched vertically by factor 1.5
A cost function \(C(x) = 100 + 5x\) increases fixed costs by €50 and variable costs by 20%. Write the new function.
Identify the transformations needed to go from \(f(x) = x^2\) to \(g(x) = -2(x + 1)^2 + 4\)
If a profit function’s graph shifts right by 10 units, what does this mean for the business?

Homework Discussion - 20 Minutes

Your questions from Tasks 03-04

Focus on transformation interpretations

Problem 4: Seasonal business model
- How did season reversal affect profits?
Problem 5: Graph interpretation
- Identifying cost-effective production ranges
Problem 7: Multi-location analysis
- Which transformations most impacted profitability?

Composition and inverses will help us model even more complex business relationships!

Function Composition

Understanding Composition

Composition models sequential processes

Definition: \((f \circ g)(x) = f(g(x))\)

Read as “f composed with g”
Apply g first, then f
Output of g becomes input of f
Order matters! \((f \circ g) \neq (g \circ f)\) usually
Business meaning: Multi-step processes

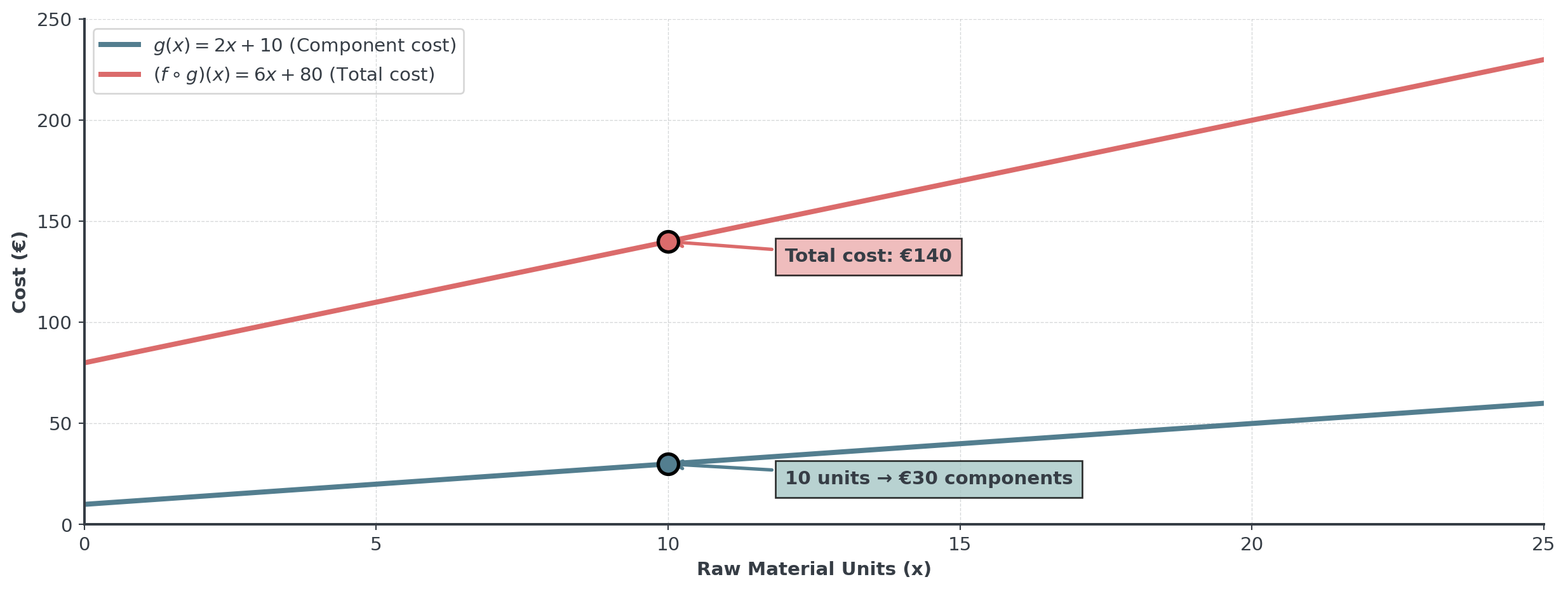
Composition Example: Supply Chain

Imagine a company manufacturing products from raw materials.

Raw materials to components: \(g(x) = 2x + 10\) (cost in €)
Components to products: \(f(y) = 3y + 50\) (cost in €)

\((f \circ g)(x) = f(g(x)) = f(2x + 10)\)
\(= 3(2x + 10) + 50\)
\(= 6x + 30 + 50\)
\(= 6x + 80\)
For 10 units raw material: Cost = €140

Supply Chain Visualization

Function Composition: Supply Chain Cost Analysis

Domain Considerations

Domain of composition can be restricted

For \((f \circ g)(x)\):

Start with domain of \(g\)
Find range of \(g\)
Intersect with domain of \(f\)
Track back to valid \(x\) values

This is not too complicated, right? Here we just need to be careful.

Example: Weight-Based Dosage and Safe Maximum

Calculate dosage based on body weight, then check safety limit

Dosage from weight: \(g(x) = 5x\) mg (5mg per kg body weight)
Safe processing: \(f(x) = \sqrt{500 - x}\) (requires total dose \(\leq 500\) mg)
Composition requires: \(5x \leq 500\), so \(x \leq 100\) kg body weight

Therefore, we cannot process a patient weighing more than 100kg, as this would be unsafe!

Quick Practice - 10 Minutes

Work individually, then we discuss

A food delivery service has the following cost structure:

Restaurant to warehouse: \(g(x) = 1.5x + 5\) (€ per order, where \(x\) is number of orders)
Warehouse to customer: \(f(y) = 2y + 8\) (€ delivery cost)

Find the composition \((f \circ g)(x)\) representing total delivery cost.
Calculate the total cost for 20 orders.
If the domain of \(g\) is \([0, 100]\) orders, what is the range of \(g\)?

Break - 10 Minutes

Inverse Functions

What is an Inverse Function?

An inverse function reverses the original function

If \(f(a) = b\), then \(f^{-1}(b) = a\). The inverse “undoes” what the original function does.

Testing for Invertibility

A function has an inverse if it’s one-to-one

Each output comes from exactly one input
Horizontal line test: Each horizontal line hits graph at most once
For continuous functions: Always increasing or always decreasing

Question: Which of the following two fulfill the one-to-one condition?

\(f(x) = 2x + 5\)
\(g(x) = x^2\)

Just make sure, you don’t use the vertical line test here!

Finding Inverse Functions

Step-by-step process

Replace \(f(x)\) with \(y\)
Swap \(x\) and \(y\)
Solve for \(y\)
Replace \(y\) with \(f^{-1}(x)\)
Verify domain and range

Looks complicated? It is actually rather easy!

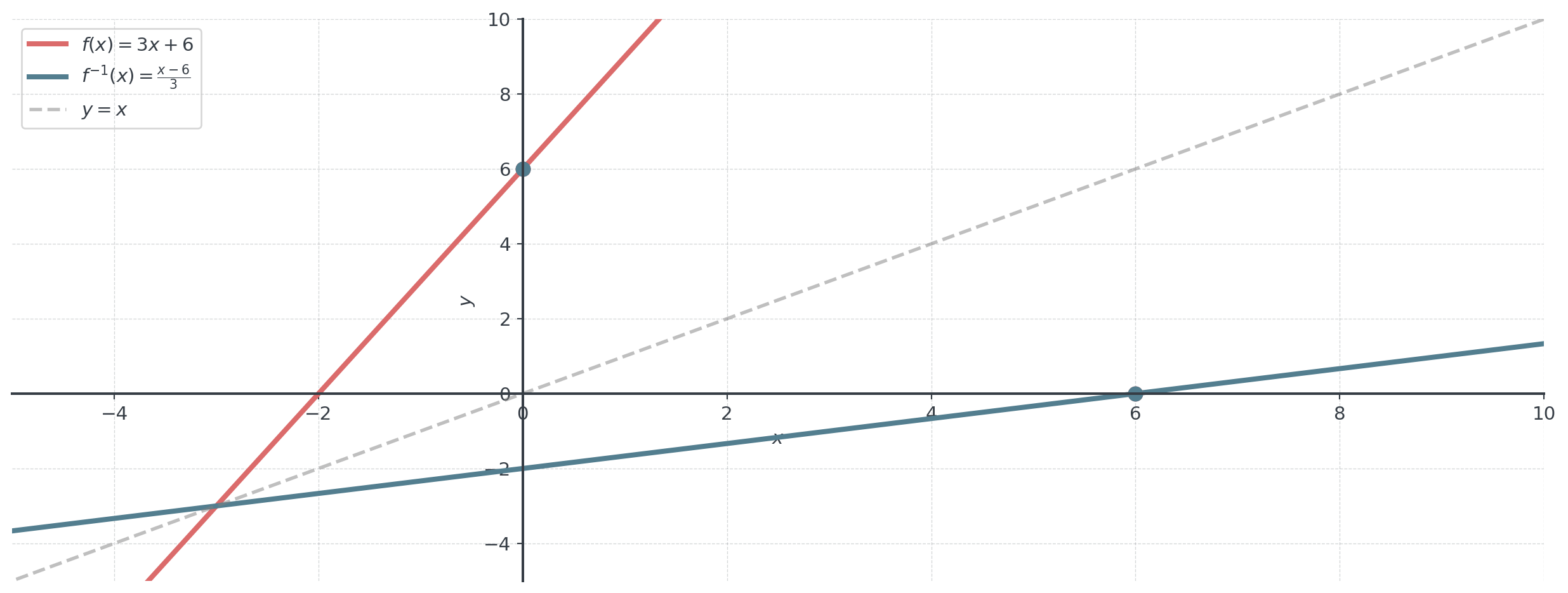
Example: Simple Linear Function

Find the inverse of \(f(x) = 3x + 6\)

\(y = 3x + 6\)
\(x = 3y + 6\) (swap \(x\) and \(y\))
\(3y = x - 6\) (solve for \(y\))
\(y = \frac{x - 6}{3}\)
Inverse: \(f^{-1}(x) = \frac{x - 6}{3}\)

Verify: \(f(f^{-1}(x)) = f\left(\frac{x-6}{3}\right) = 3 \cdot \frac{x-6}{3} + 6 = x - 6 + 6 = x\) ✓

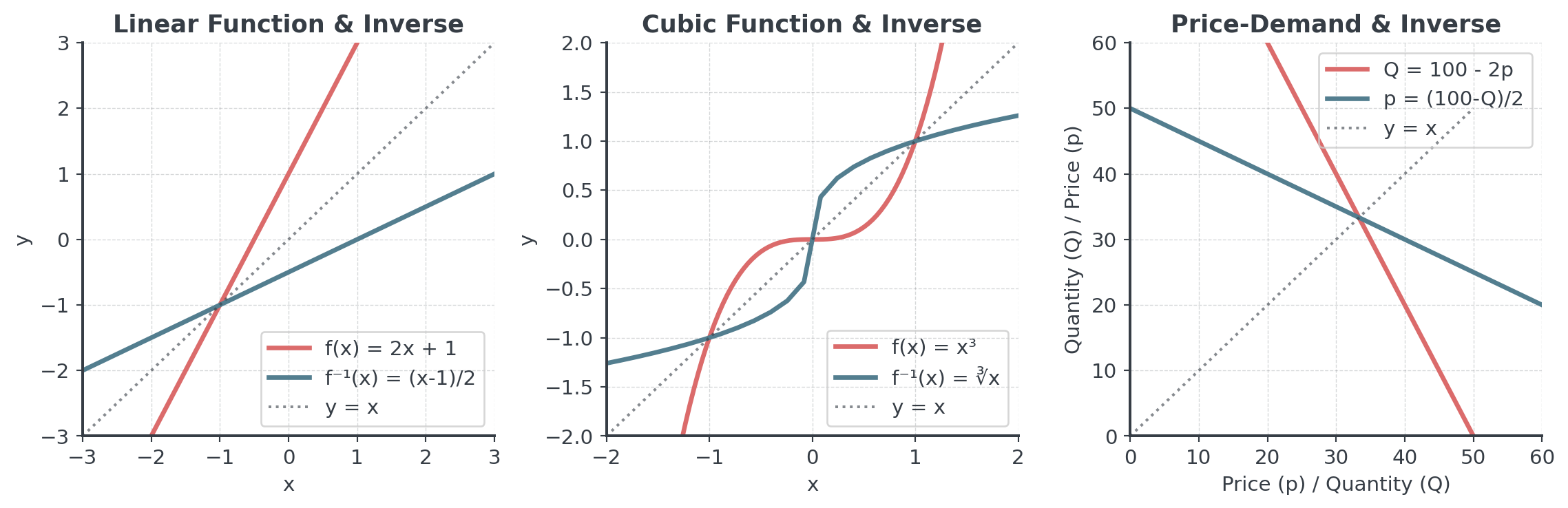
Visualizing the Inverse

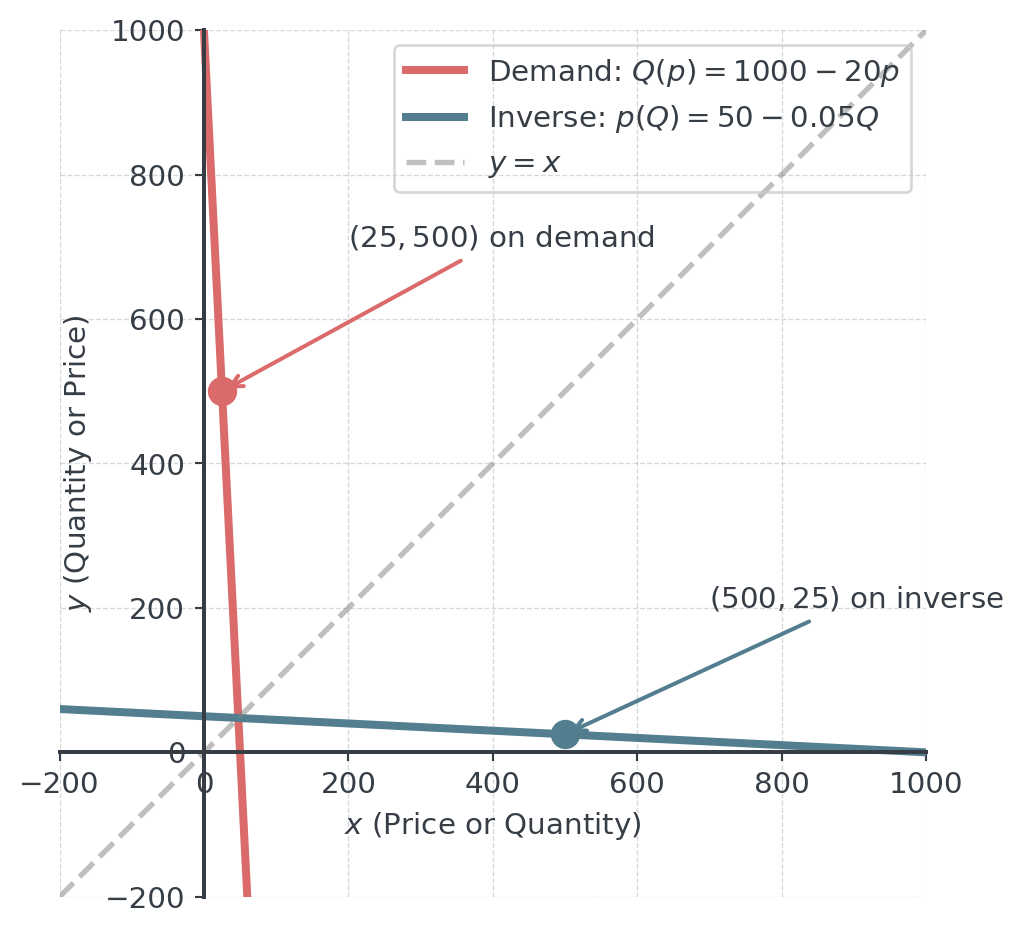
Function \(f(x) = 3x + 6\) and its inverse \(f^{-1}(x) = \frac{x-6}{3}\) reflected over \(y=x\)

Example: Price-Demand Inverse

Demand function: \(Q = 1000 - 20p\)

\(y = 1000 - 20p\)
\(x = 1000 - 20p\) (swap)
\(x - 1000 = -20p\)
\(p = 50 - 0.05x\)
Inverse: \(p(Q) = 50 - 0.05Q\)

What does this mean? It gives the price needed for specific quantity!

Visualizing Price-Demand Relationship

Demand function and its inverse reflected over the line \(y=x\).

Advanced Graphing Techniques

Graphing Composed Functions

Build graphs step by step

Strategy for graphing \((f \circ g)(x)\):

Graph \(g(x)\) first
For key points, find \(g(x)\) values
Apply \(f\) to those values
Plot resulting points
Consider domain restrictions

Graphing Inverse Functions

Use reflection property

To graph \(f^{-1}(x)\) from \(f(x)\):

Plot original function \(f(x)\)
Draw line \(y = x\)
Reflect \(f(x)\) over this line
Key points: \((a, b)\) on \(f\) → \((b, a)\) on \(f^{-1}\)
Domain of \(f\) = Range of \(f^{-1}\)
Range of \(f\) = Domain of \(f^{-1}\)

Guided Practice - 25 Minutes

Individual Exercise Block

Work alone for 15 minutes, then discuss for 10 minutes

Given \(f(x) = 2x + 3\) and \(g(x) = x^2 - 1\):
1. Find \((f \circ g)(x)\) and evaluate \((f \circ g)(2)\)
2. Find \((g \circ f)(x)\) and evaluate \((g \circ f)(2)\)
A company converts raw materials through two stages:
- Stage 1: \(C_1(x) = 50x + 200\) (process cost in €)
- Stage 2: \(C_2(y) = 2y + 500\) (assembly cost in €)
- Find the total cost function and cost of 100 units of material.
Find the inverse of \(f(x) = \frac{2x + 3}{5}\) and verify your answer.

Coffee Break - 15 Minutes

Business Process Modeling

Multi-Step Processes

Complex business operations as function chains

Question: Does you have any example that involves multiple stages?

Examples of composition in business:

Manufacturing: Raw materials → Components → Products
Finance: Local currency → Foreign currency → Investment
Retail: Wholesale price → Retail price → After-tax price
Marketing: Leads → Conversions → Revenue

Supply Chain Example

Three-Stage Production from Cost to Price

Supplier: Raw materials at \(p_r = 10 + 0.5x\) (€ per kg)
Processor: Converts at 80% efficiency, adds €20/kg
Retailer: Marks up 50%, adds €15 flat fee

Let’s build the final price function together:

After supplier: Cost = \(x(10 + 0.5x) = 10x + 0.5x^2\)
After processor: Cost = \(0.8(10x + 0.5x^2) + 20x\)
After retailer: Price = \(1.5[(10x + 0.5x^2) + 20x] + 15\)

Inverse Functions in Business

Common business inverses

Demand ↔︎ Price: Know one, find the other
Cost ↔︎ Quantity: Determine production from budget
Profit ↔︎ Sales: Find required sales for target profit
Break-even analysis: Reverse engineer requirements

Also, it could just be a task you are given.

Problem-Solving - 30 Minutes

International Business Model I

The Scenario: Global E-Commerce Platform

An e-commerce company operates internationally with these functions:

Pricing Model:

Base price in USD: \(P(x) = 50 + 0.8x\) where \(x\) is quantity
EUR conversion: \(E(p) = 0.85p\)
UK markup: \(U(p) = 1.2p + 10\)

International Business Model II

The Scenario: Global E-Commerce Platform

Shipping Costs:

Weight calculation: \(W(x) = 0.5x + 2\) (kg)
Shipping cost: \(S(w) = 15w + 25\) (€)

Customer Demand:

At total price \(T\): \(D(T) = 5000 - 20T\) units per month

Your Tasks

If you like, you can work in groups

Find the total price function for EU customers (product + shipping) as a function of quantity \(x\).
Find the inverse of the demand function. What does it represent?
Create a composite function that gives monthly demand based on quantity ordered.
If the company wants exactly 2000 units demanded per month, what should the quantity per order be?
The company can only process orders where total price leads to positive demand. Find the maximum viable order quantity.

Section 03 Synthesis

Your Function Toolkit

Complete arsenal for business modeling

Function basics: Notation, domain, range
Linear functions: Constant rates, equilibrium
Quadratic functions: Optimization, vertex
Transformations: Adapting to change
Composition: Multi-step processes
Inverses: Reversing calculations

Key Business Applications

From this section, you can now:

Model costs, revenue, and profit
Find market equilibrium
Optimize prices and quantities
Adapt models for new conditions
Chain processes together
Reverse-engineer requirements

Wrap-Up

Key Takeaways

Composition models sequential processes
Order matters: \((f \circ g) \neq (g \circ f)\)
Inverses reverse calculations
One-to-one functions are invertible
Graphical tools reveal function relationships
Business processes often involve multiple functions

Final Assessment

5 minutes - Individual work

A retailer has:

Cost function: \(C(x) = 20x + 500\)
Price function: \(P(x) = 50 - 0.5x\)
Revenue: \(R(x) = x \cdot P(x)\)

Express revenue as a function of \(x\) explicitly
Find the inverse of the cost function
If the retailer has a budget of €2,500, how many units can they stock?

Next Session Preview

Session 03-06: Mock Exam 02

Key concepts you should master

Function fundamentals: Domain, range, notation
Linear functions: Supply/demand, equilibrium, CVP analysis
Quadratic functions: Vertex, optimization, profit maximization
Transformations: Shifts, stretches, business interpretations
Composition & Inverses: Multi-step processes, reversing calculations
Graphical analysis: Reading and interpreting business graphs

Exam Preparation Tips

Function Problem Strategies

Systematic approaches for success

Start with domain: Always check restrictions first
Identify function type: Linear, quadratic, or composed?
Business context: What does each variable represent?
Optimization: Remember vertex formula \(x = -\frac{b}{2a}\)
Verify results: Do answers make business sense?

Common Pitfalls to Avoid

Learn from typical mistakes

Not follwing the instructions: Read the tasks carefully!
Composition order: Remember \((f \circ g) \neq (g \circ f)\)
Units confusion: Track currency vs. quantity units
Graph interpretation: Missing key features
Business meaning: Failing to interpret mathematical results

Homework Assignment: Complete Tasks 03-05!