Session 03-01 - Function Concepts & Business Modeling
Section 03: Functions as Business Models
Welcome to Functions!
Introduction
- From equations to functions: A powerful generalization
- We’ve solved equations; now we’ll model relationships
- Functions as business tools
- Cost, revenue, and profit modeling
- Mathematical used to model real-world applications
- Essential for business decision-making
Entry Quiz - 10 Minutes
Quick Review from Section 02
Work individually, then we compare together
\[\begin{cases} 2x + 3y = 18 \\ x - y = 1 \end{cases}\]
A company’s costs increase exponentially according to \(C = 1000 \cdot 1.05^t\). After how many years will costs double?
Solve for \(x\): \(\log_2(x+3) + \log_2(x-1) = 3\)
Translate: “The profit equals revenue minus costs, where revenue is 50 euros per unit and costs include a fixed cost of 1000 euros plus 30 euros per unit.”
Section 02 Review
Your open questions
Ask your questions about the past sections!
- Is there something you are not feeling comfortable with?
- Has there been a task in the exam you found hard?
- Is there any topic you would like to have repeated?
This is your chance to have something repeated!
From Equations to Functions
What is a Function?
A function is a rule that assigns to each input exactly one output
- Equation perspective: \(y = 2x + 5\) (a relationship)
- We’ve been solving these for specific values
- Function perspective: \(f(x) = 2x + 5\) (a machine)
- Input any \(x\), get exactly one output \(f(x)\)
- Business perspective: A model of cause and effect
- Input: production quantity → Output: total cost
Question: Does this make sense for you?
Function Notation
Symbolic language for modeling
\(f(x) = 2x^2 - 3x + 1\)
- \(f\) is the function name (like naming a business model)
- \(x\) is the input variable (independent variable)
- \(f(x)\) is the output value (dependent variable)
Read as: “f of x equals…”
To find \(f(3)\): \(f(3) = 2(3)^2 - 3(3) + 1 = 18 - 9 + 1 = 10\)
Multiple Function Names
Different functions model different business aspects
- Cost function: \(C(x)\) = total cost for \(x\) units
- Revenue function: \(R(x)\) = total revenue from \(x\) units
- Profit function: \(P(x) = R(x) - C(x)\)
- Demand function: \(D(p)\) = quantity demanded at price \(p\)
So far not too difficult, right?
Business Example
A bakery has:
- Fixed costs: 500€ per day
- Variable costs: 2€ per pastry
- Selling price: 5€ per pastry
Question: What is the cost, the revenue and the profit function?
Quick Practice - 10 Minutes
Function Evaluation Practice
Work individually for 5 minutes, then we discuss
Given the functions:
- \(f(x) = 3x^2 - 2x + 1\)
- \(g(x) = \frac{x+4}{x-2}\)
Calculate:
- \(f(0)\), \(f(2)\), and \(f(-3)\)
- \(g(5)\) and \(g(0)\)
Break - 10 Minutes
Domain and Range
Understanding Domain
The domain is the set of all possible input values
- Mathematical restrictions:
- Cannot divide by zero
- Cannot take square root of negative (in real numbers)
- Logarithm requires positive argument
- Business restrictions:
- Cannot produce negative quantities
- Limited production capacity
- Budget constraints
Domain Examples
For \(f(x) = \frac{1}{x-3}\):
- Denominator cannot be zero
- \(x - 3 \neq 0\)
- \(x \neq 3\)
- Domain: \(\mathbb{R} \setminus \{3\}\) or \((-\infty, 3) \cup (3, \infty)\)
For \(g(x) = \sqrt{2x + 6}\):
- Argument must be non-negative
- \(2x + 6 \geq 0\)
- \(x \geq -3\)
- Domain: \([-3, \infty)\)
Production function \(P(x) = 100\sqrt{x}\) where \(x\) is hours of labor:
- Mathematical: \(x \geq 0\) (square root)
- Practical: \(0 \leq x \leq 24\) (hours per day)
- Domain: \([0, 24]\)
Understanding Range
The range is the set of all possible output values
- What values can the function actually produce?
- Often harder to find than domain
- Depends on the function’s behavior
- Critical for understanding business limitations
Range = Output!
Finding Range Examples
For \(f(x) = x^2 + 2\):
- When \(x = 0\): \(f(0) = 2\)
- Values grow larger as \(|x|\) increases
- Range: \([2, \infty)\)
- Note, we’ll learn to find exact minimum points soon!
For \(g(x) = \frac{1}{x}\) with domain \(x \neq 0\):
- Can be any value except 0
- Range: \(\mathbb{R} \setminus \{0\}\)
Monthly membership revenue \(R(x) = 50x\) where \(x\) is number of members:
- Minimum: \(R(0) = 0\) (no members)
- Increases linearly without bound
- Range: \([0, \infty)\)
- Practical limit depends on capacity
Function Representations
Four Ways to Represent Functions
Each representation offers unique insights
- Verbal: “Base costs of 100 which increase by 3 for each additional unit”
- Algebraic: \(C(x) = 100 + 3x\)
- Numerical: Table of values
- Graphical: Visual representation
Question: How would you represent this function as table and as graph?
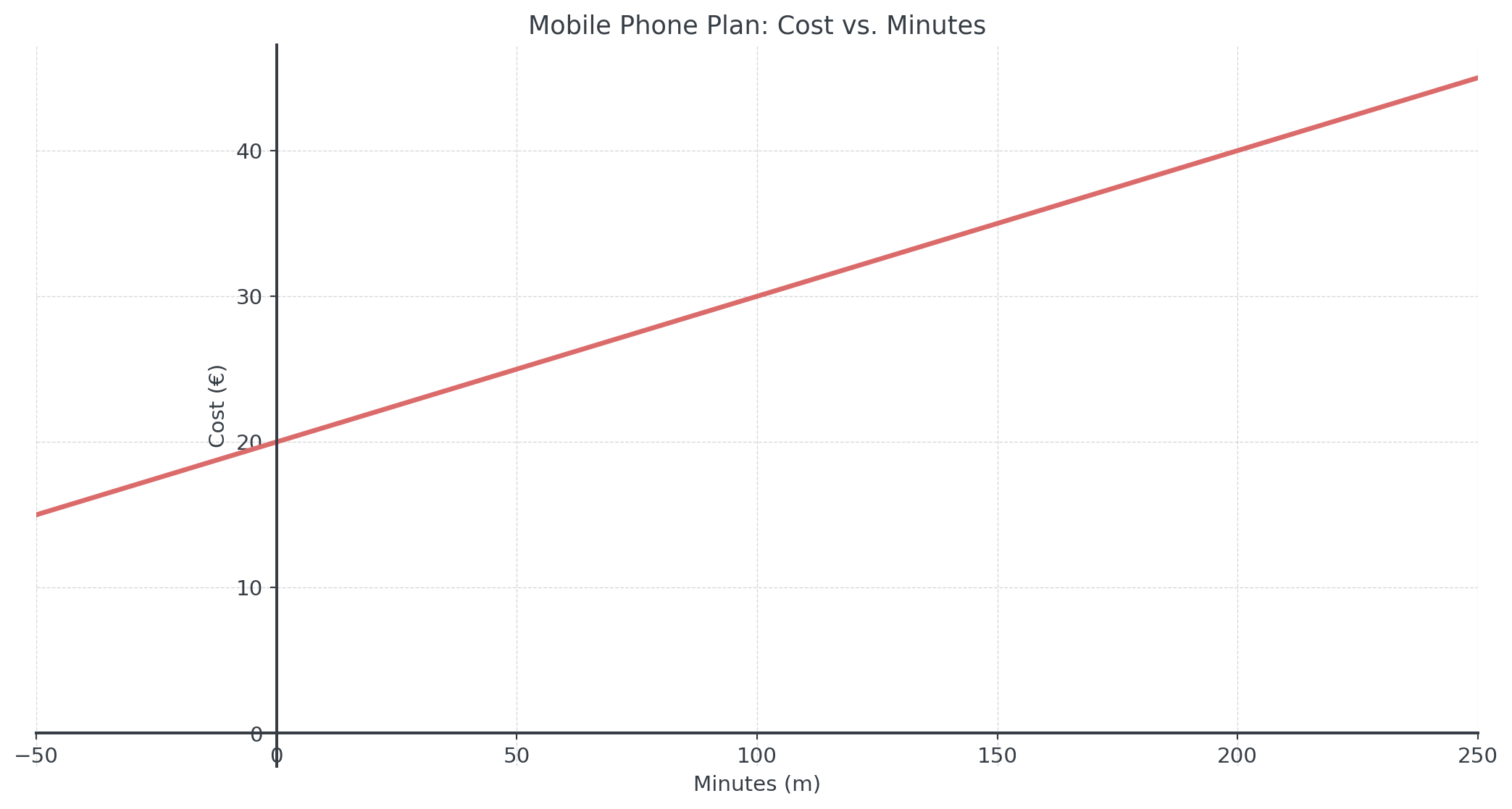
Example: Mobile Phone Plan
Scenario: Mobile plan costs 20€ base fee plus 0.10€ per minute.
Question: How would you represent this as a function, as a table and as a graph?
Graphical Representation
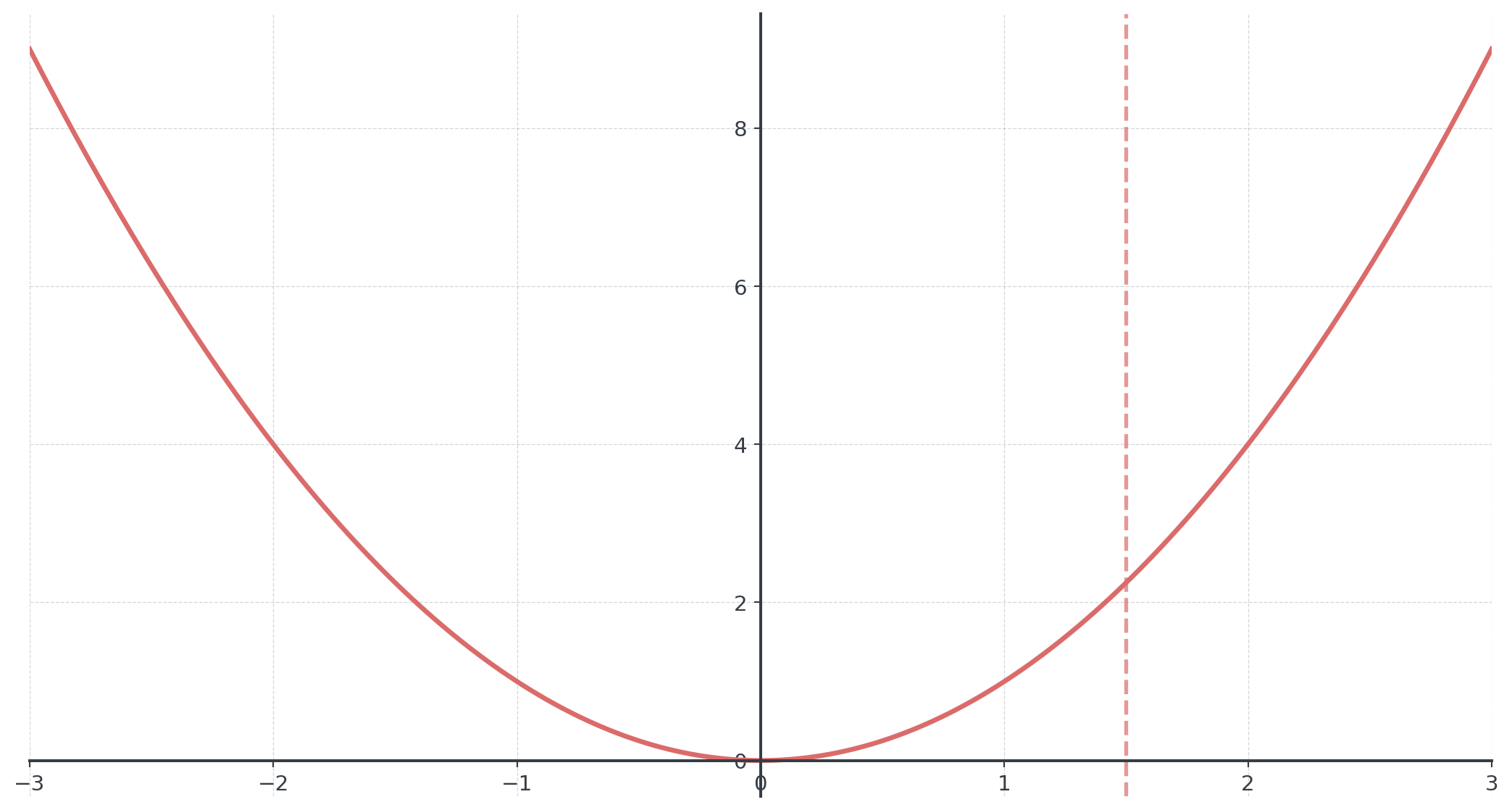
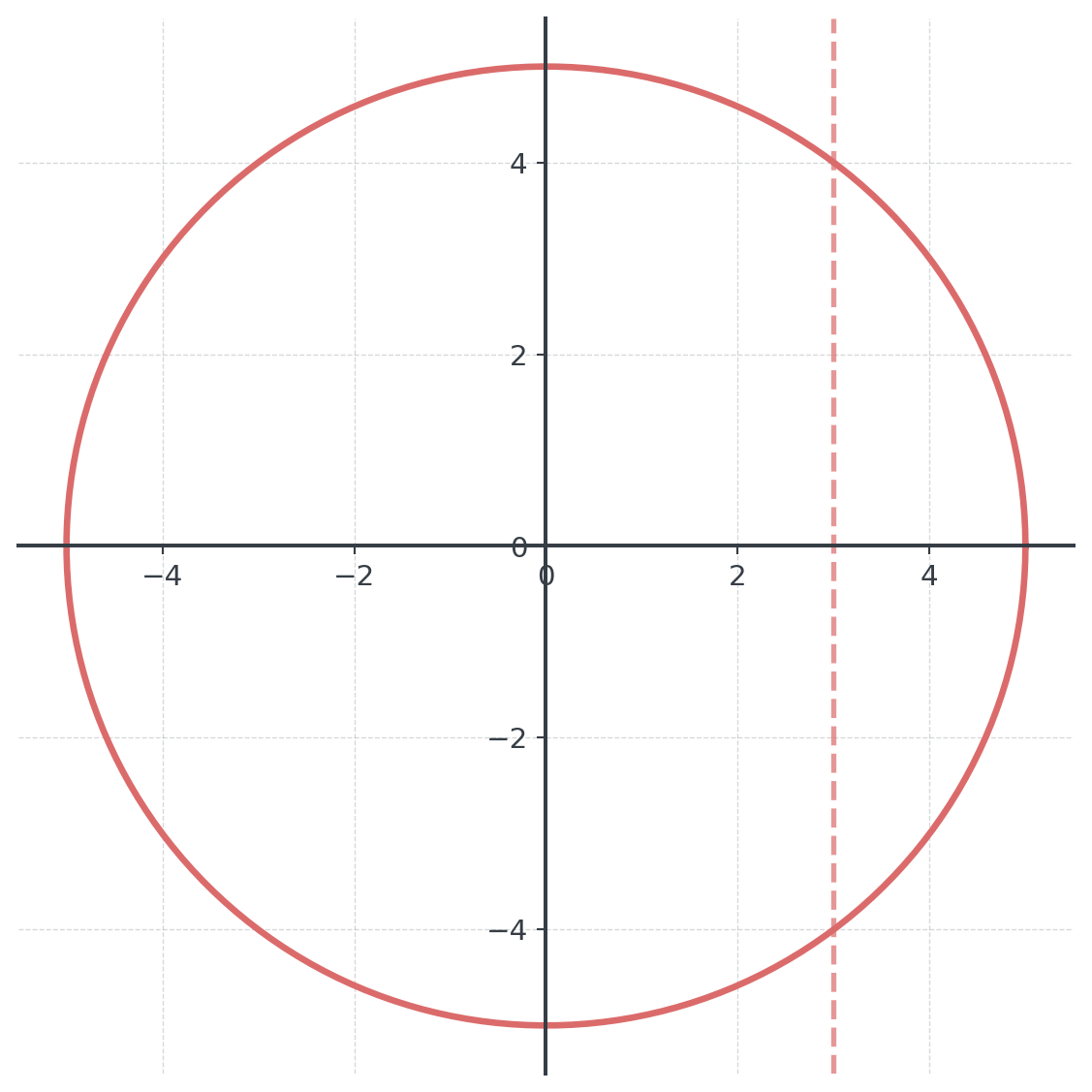
The Vertical Line Test
A graph only represents a function if every possible vertical line intersects it at most once
- Why? Each input must have exactly one output
- Pass: Linear, quadratic, exponential graphs
- Fail: Circles, sideways parabolas
- Business implication: No ambiguity in predictions
Is this a function?
What about this?
Guided Practice - 25 Minutes
Individual Exercise Block
Work alone for 15 minutes
Find the domain of: \(f(x) = \frac{x+2}{x^2-4}\)
Cost function is \(C(x) = 1500 + 25x\) and revenue is \(R(x) = 40x\)
- Find the profit function \(P(x)\)
- What is the break-even point?
- What is a reasonable domain for this model?
Given the function \(g(x) = 2x + 8\):
- Find the domain and range
- Find where \(g(x) = 20\)
Business Applications
Cost Functions in Detail
Understanding the structure of business costs
\[C(x) = \text{Fixed Costs} + \text{Variable Costs}\]
- Fixed Costs (FC): Rent, insurance, salaries
- Independent of production level
- Variable Costs (VC): Materials, hourly wages, utilities
- Proportional to production
- Total Cost: \(C(x) = FC + VC \cdot x\)
- Average Cost: \(AC(x) = \frac{C(x)}{x}\)
Revenue and Demand
The relationship between price and quantity
- Simple model: \(R(x) = p \cdot x\) (fixed price)
- Linear revenue function
- Reality: Price often depends on quantity sold
- Higher supply → lower price
- This creates more complex models
- Preview: In Session 03-03, we’ll explore quadratic models
- These allow us to find optimal quantities
- Essential for maximizing profit
Combining Functions
Example: Concert Tickets
- Fixed price: 40€ per ticket
- Fixed costs: 10,000€
- Variable costs: 10€ per ticket
- Revenue: \(R(x) = 40x\) (linear function)
- Cost: \(C(x) = 10000 + 10x\) (linear function)
- Profit: \(P(x) = R(x) - C(x) = 40x - (10000 + 10x)\)
- Simplified: \(P(x) = 30x - 10000\) (also linear!)
- Break-even: When \(P(x) = 0\), so \(x = 333.33\) → need 334 tickets
Collaborative Problem-Solving
Group Activity: Startup Analysis
The Scenario
A startup produces custom phone cases:
- Fixed monthly costs: 3,000€ (rent, equipment, insurance)
- Material cost per case: 8€
- Labor cost per case: 7€
- They plan to sell at a fixed price of 35€ per case
Your Tasks
Work in groups of if you like
- Develop the cost function \(C(x)\)
- Develop the revenue function \(R(x)\)
- Find the profit function \(P(x)\)
- Determine the break-even quantity (where \(P(x) = 0\))
- If they can produce maximum 500 cases per month, what’s their maximum possible profit?
Coffee Break - 15 Minutes
Practice Tasks
Identifying Functions (x)
Work individually and then we compare.
Determine whether each relation represents a function. If it is not a function, explain why using the vertical line test concept.
- \(y = 4x - 7\)
- \(x^2 + y^2 = 25\)
- \(y = |x - 2|\)
- \(x = y^2 + 1\)
Fitness Center Membership Model
A center has collected data on how membership varies with price.
| Monthly Fee (€) | Number of Members |
|---|---|
| 30 | 400 |
| 40 | 350 |
| 50 | 300 |
| 60 | 250 |
The fitness center has:
- Fixed monthly costs: €15,000
- Variable costs: €5 per member
Your Tasks
Work in groups for 20 minutes
- Show that this data represents a function with monthly fee as input and number of members as output
- Write the function \(N(p)\) where \(p\) is the monthly fee (assuming a linear relationship)
- Find a reasonable domain for this business context
- Write the profit function \(P(p)\) in terms of the monthly fee \(p\)
Wrap-Up
Key Takeaways
- Functions model relationships between variables
- Domain and range define boundaries of our models
- Business applications require multiple functions working together
- The same relationship can be represented in multiple ways
- Real-world constraints affect mathematical models
Final Assessment
5 minutes - Individual work
A local gym has fixed costs of 5000€ per month and variable costs of 10€ per member. They charge 40€ per member per month.
- Write the cost function \(C(x)\) where \(x\) is the number of members
- Write the revenue function \(R(x)\)
- How many members are needed to break even?
Next Session Preview
03-02: Linear Functions & Economic Applications
- Deep dive into linear functions
- Supply and demand curves
- Market equilibrium
- Linear regression basics
- Cost-volume-profit analysis
Homework Assignment: Complete Tasks 03-01!
Session 03-01 - Function Concepts & Business Modeling | Dr. Nikolai Heinrichs & Dr. Tobias Vlćek | Home