Tutorial XII - Passenger Flow Control in Urban Rail

Applied Optimization with Julia

Introduction

Consider the depicted ‘Golden Line’ on the left with 4 different stations A, B, C, D. For an upcoming timeframe of 10 minutes divided into 10 periods, the transportation demand is going to exceed the available capacity of the network and each origin-destination pair will be requested by at least 1 passenger. To handle the inflow, queues will be put in place at each metro station.

The Challenge

Your task is to minimize the queues without exceeding the available transport capacity of max. 100 passengers per minute of each arc. A safety buffer per arc is not needed. Each station layout is excellent, with sufficient stairs and escalators. Thus, the station itself is fully capable of handling any inflow that may result from the optimized restricted inflow. Nonetheless, queues are still necessary as the arcs cannot handle each input.

1. Flow Analysis

Suppose we are in minute 7 at the arc of (D,A). Which inflows from which stations are going to impact the flow into the arc in this minute?

Write out the set \(\mathcal{R}_{(D,A),7}\) and shortly explain your answer. You can write out the set in a comment, for example like this:

#=
{(A,B,1), (B,C,1), (C,D,1)}
=#

Tip

To solve this task, it might be helpful to work with paper and pen to sketch the problem.

#=
YOUR ANSWER BELOW


=#

2. Inflow Control

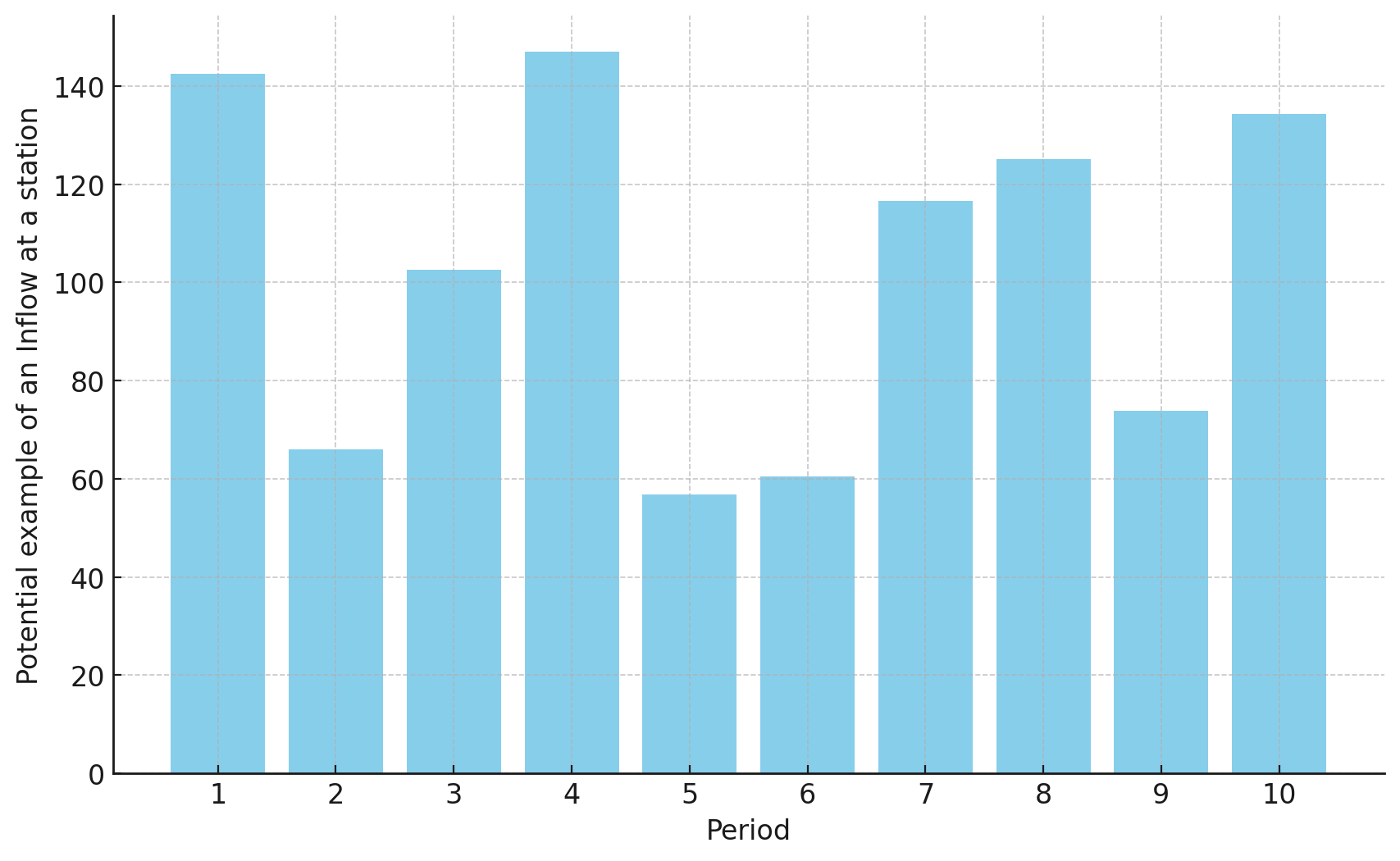
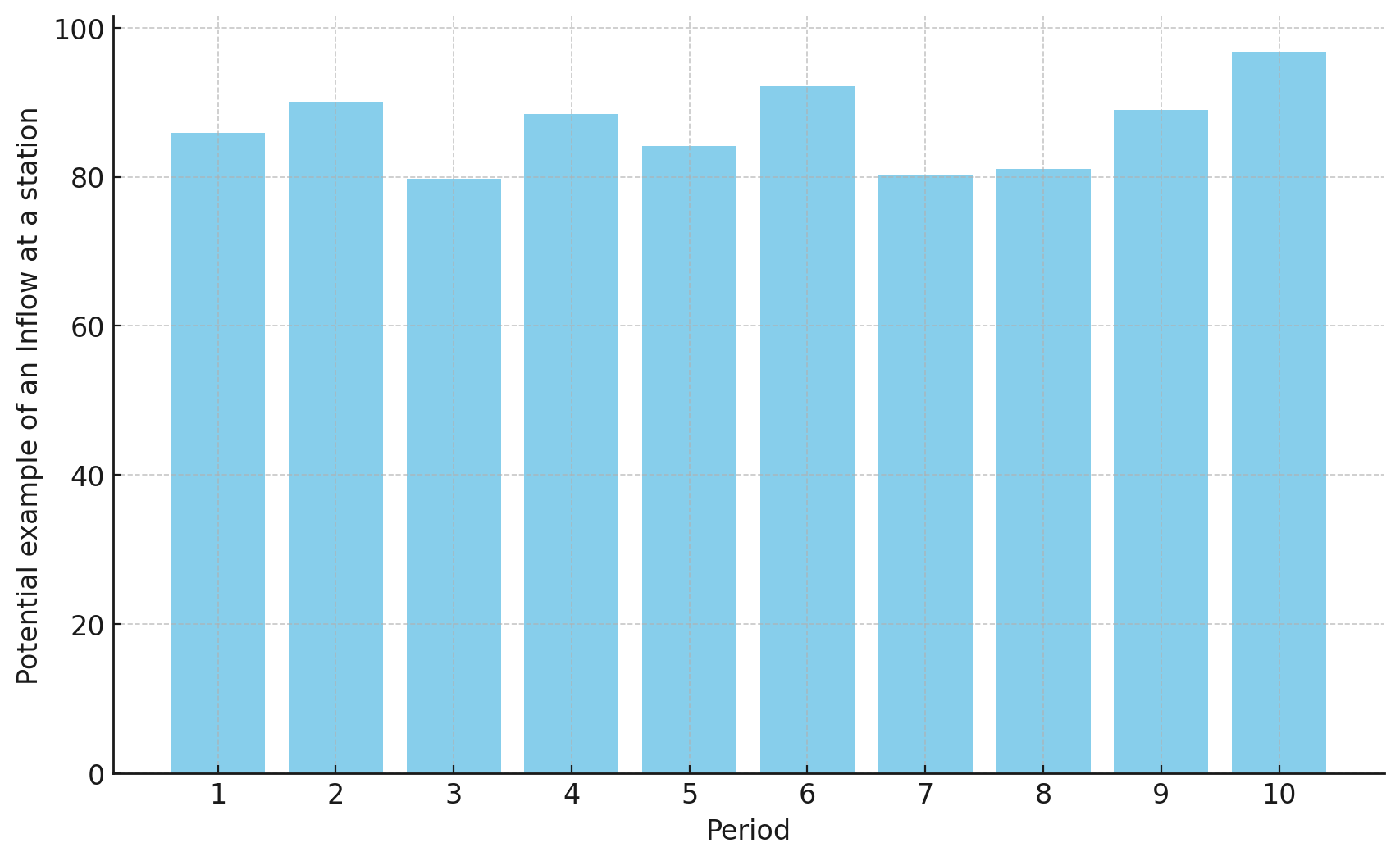
As there is a rather large fluctuation of allowed inflow between periods, you are asked to introduce new constraints for the model. In the first period, the inflow at each station is supposed to be unrestricted. Thereafter, it is maximally allowed to change by 20 persons in both directions per period at each station.

Can you write out the decision variables and the additional constraints for the model as JuMP constraints?

Tip

You don’t need to solve the model or define the objective function. You just need to constraint the fluctuations and add the appropriate variables.

using JuMP
metro_model = Model()

# YOUR CODE BELOW

3. Bidirectional Flow

The metro was improved and there is now the possibility to travel in both directions. How would this change the set \(\mathcal{R}_{(MD,MA),7}\) from 1.?

Write out the new set \(\mathcal{R}_{(D,A),7}\) manually and shortly explain your answer.

#=
# YOUR ANSWER BELOW

=#

4. Capacity Analysis

Although the system is two-directional now, the overall number of trains of the metro provider has not changed. Would the change from a one-directional metro system to a two-directional metro system decrease the likelihood of crowd-accidents due to insufficient arc-capacities?

Please explain your answer in a few sentences.

#=
# YOUR ANSWER BELOW

=#

5. Computing the Set \(\mathcal{R}_{e,t}\)

Can you compute the set \(\mathcal{R}_{e,t}\) for the one-directional flow? Generate a dictionary \(R\) that contains \(e \times t\) entries. Each entry \(r_{e,t}\) should contain a vector with all origin-destination pairs and the corresponding time period saved as a tuple. Use the results to check your answer from the first task.

Note

This task can be a bit tricky, as it is a bit of a challenge. But as it is the last tutorial, I figured a small challenge is fine.

# YOUR CODE BELOW

If you encounter any difficulties ad cannot solve the problem, please document your issues here:

#=



=#

Solutions

You will likely find solutions to most exercises online. However, I strongly encourage you to work on these exercises independently without searching explicitly for the exact answers to the exercises. Understanding someone else’s solution is very different from developing your own. Use the lecture notes and try to solve the exercises on your own. This approach will significantly enhance your learning and problem-solving skills.

Remember, the goal is not just to complete the exercises, but to understand the concepts and improve your programming abilities. If you encounter difficulties, review the lecture materials, experiment with different approaches, and don’t hesitate to ask for clarification during class discussions.

Later, you will find the solutions to these exercises online in the associated GitHub repository, but we will also quickly go over them in next week’s tutorial. To access the solutions, click on the Github button on the lower right and search for the folder with today’s lecture and tutorial. Alternatively, you can ask ChatGPT or Claude to explain them to you. But please remember, the goal is not just to complete the exercises, but to understand the concepts and improve your programming abilities.