Session 06-03 - Area Problems & Basic Applications

Section 06: Integral Calculus

Dr. Nikolai Heinrichs & Dr. Tobias Vlćek

Entry Quiz - 10 Minutes

Quick Review from Session 06-02

Test your understanding of Definite Integrals

1. Evaluate \(\int_1^4 (3x^2 - 2x) \, dx\)

2. If \(\int_0^5 f(x) \, dx = 18\) and \(\int_3^5 f(x) \, dx = 7\), find \(\int_0^3 f(x) \, dx\)

3. What does \(\int_a^b f'(x) \, dx\) represent geometrically and algebraically?

4. For \(f(x) = x - 2\) on \([0, 4]\), is the signed area positive, negative, or zero?

Homework Discussion - 15 Minutes

Your questions from Session 06-02

Focus on FTC and definite integrals

• Evaluating definite integrals with bounds
• Signed area vs. total area distinction
• Properties of definite integrals
• Net change applications

Today we focus on area calculations and introduce exponential and logarithmic integrals!

Learning Objectives

What You’ll Master Today

• Calculate area under a curve above the x-axis
• Handle regions where the function is below the x-axis
• Find total area by splitting at zeros
• Integrate exponential functions \(\int e^{ax} \, dx\)
• Integrate \(\frac{1}{x}\) to get natural logarithm
• Apply area concepts to business problems
• Interpret accumulated quantities from rate functions

Area calculations are one of the most common applications of integration!

Part A: Area Under a Curve

When \(f(x) \geq 0\)

Simple case: When \(f(x) \geq 0\) on \([a, b]\), the definite integral gives the area directly.

\[\text{Area} = \int_a^b f(x) \, dx\]

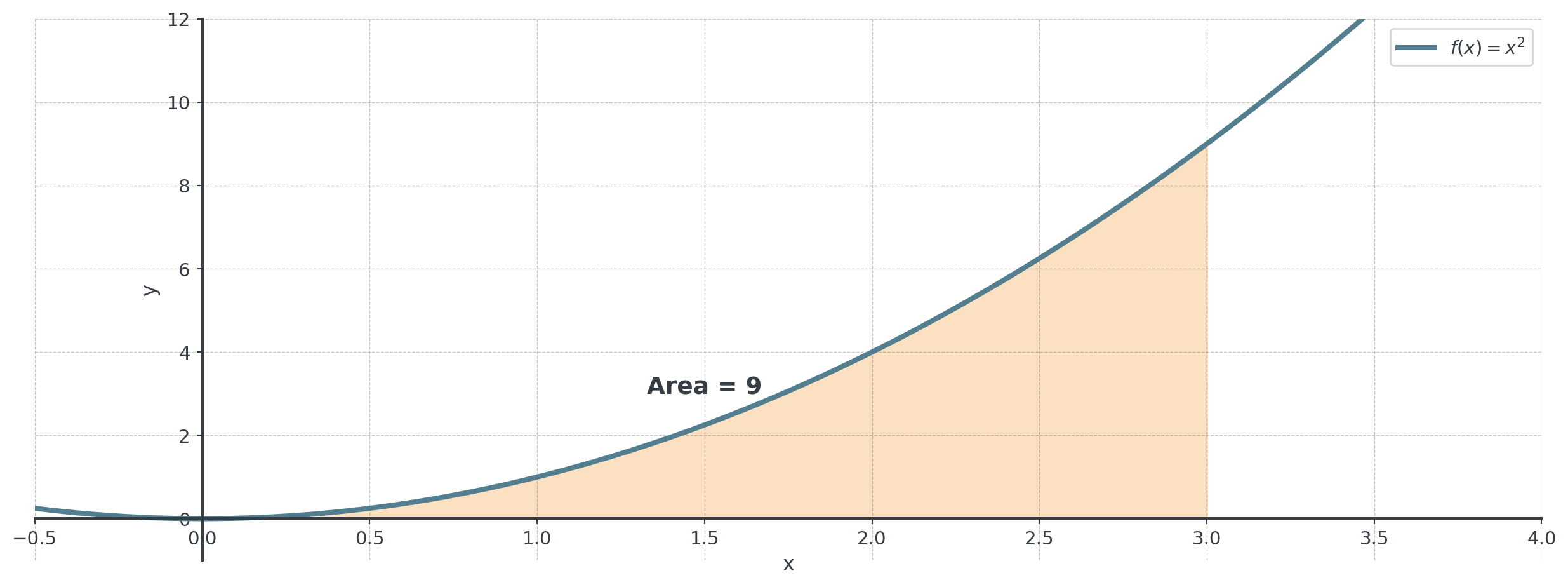
Example: Area Under a Parabola I

Find the area under \(f(x) = x^2\) from \(x = 0\) to \(x = 3\).

Solution:

\[\text{Area} = \int_0^3 x^2 \, dx = \frac{x^3}{3} \Big|_0^3 = \frac{27}{3} - 0 = 9\]

Example: Area Under a Parabola II

Find the area under \(f(x) = x^2\) from \(x = 0\) to \(x = 3\).

Part B: Area When \(f(x) < 0\)

The Sign Problem

When \(f(x) < 0\): The definite integral gives a negative value!

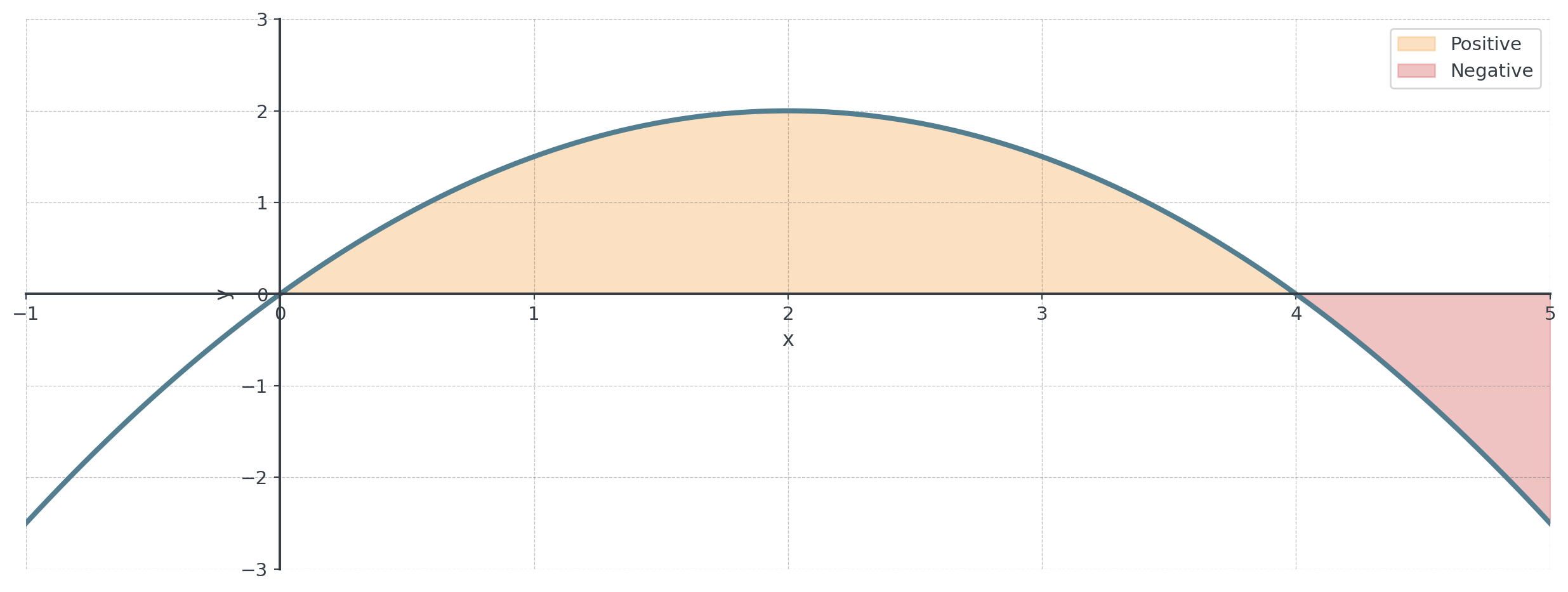
Definite integral ≠ Total area when function crosses the x-axis!

Total Area Strategy

To find total (unsigned) area:

1. Find where \(f(x) = 0\) (zeros/roots)
2. Split the integral at each zero
3. Take absolute value of each piece
4. Add all the positive values

\[\text{Total Area} = \sum |\text{each region}|\]

Example: Finding Total Area

Total area between \(f(x) = x^2 - 4\) and x-axis from \(x = 0\) to \(x = 3\)?

Step 1: Find zeros: \(x^2 - 4 = 0 \implies x = \pm 2\)

• Only \(x = 2\) is in \([0, 3]\).

Step 2: Determine signs:

• \(f(1) = -3 < 0\) (below x-axis on \([0, 2]\))
• \(f(3) = 5 > 0\) (above x-axis on \([2, 3]\))

Completing the Calculation

Step 3: Calculate each piece:

\[\int_0^2 (x^2 - 4) \, dx = \left[\frac{x^3}{3} - 4x\right]_0^2 = \frac{8}{3} - 8 = -\frac{16}{3}\]

\[\int_2^3 (x^2 - 4) \, dx = \left[\frac{x^3}{3} - 4x\right]_2^3 = (9 - 12) - (\frac{8}{3} - 8) = -3 + \frac{16}{3} = \frac{7}{3}\]

Step 4: Total area:

\[\text{Total Area} = \left|-\frac{16}{3}\right| + \frac{7}{3} = \frac{16}{3} + \frac{7}{3} = \frac{23}{3}\]

Visualization

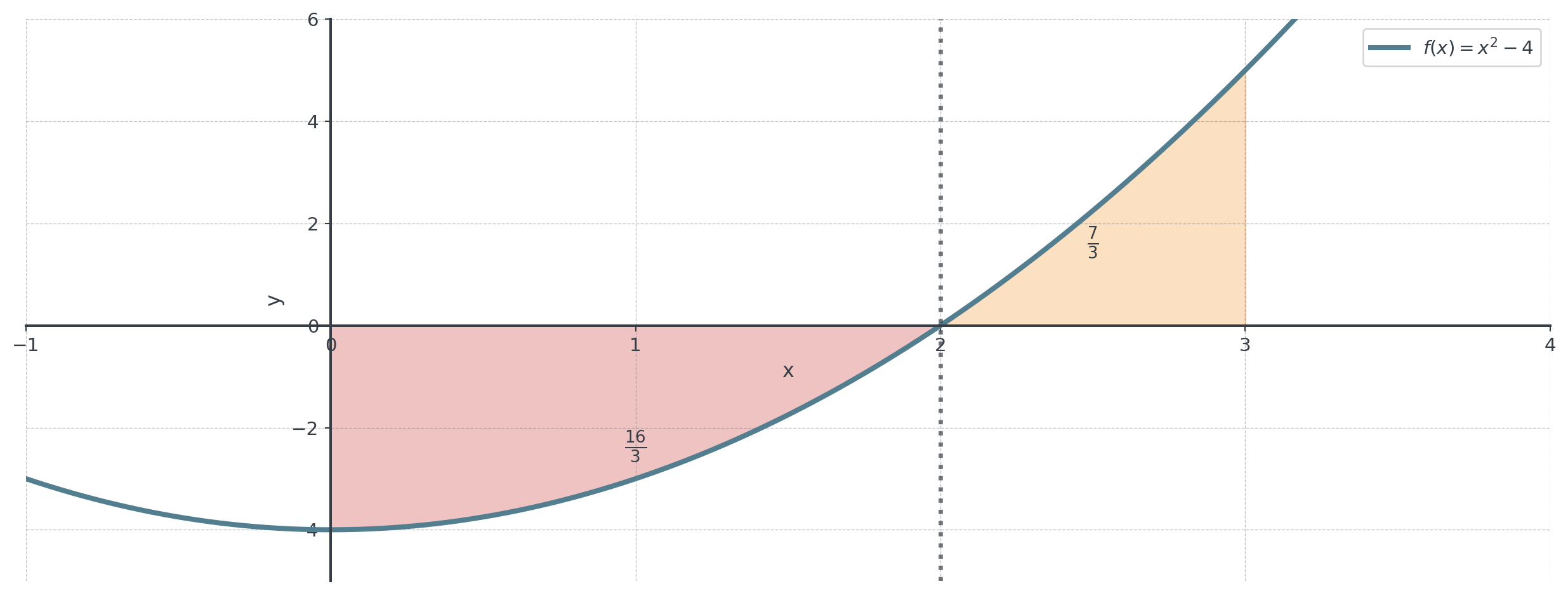
Total Area = \(\frac{16}{3} + \frac{7}{3} = \frac{23}{3} \approx 7.67\)

Break - 10 Minutes

Part C: Exponential Integrals

Integrating \(e^x\)

Recall: \(\frac{d}{dx}[e^x] = e^x\)

Therefore:

\[\int e^x \, dx = e^x + C\]

The exponential function is its own antiderivative!

Integrating \(e^{ax}\)

For \(e^{ax}\) where \(a\) is a constant:

\[\int e^{ax} \, dx = \frac{1}{a} e^{ax} + C\]

Verification: \(\frac{d}{dx}\left[\frac{1}{a}e^{ax}\right] = \frac{1}{a} \cdot a \cdot e^{ax} = e^{ax}\) ✓

Trick: Divide by the coefficient of \(x\) in the exponent.

Examples: Exponential Integrals

Example 1: \(\int e^{3x} \, dx\)

• \(\frac{1}{3}e^{3x} + C\)

Example 2: \(\int e^{-2x} \, dx\)

• \(\frac{1}{-2}e^{-2x} + C = -\frac{1}{2}e^{-2x} + C\)

Example 3: \(\int 4e^{5x} \, dx\)

• \(4 \cdot \frac{1}{5}e^{5x} + C = \frac{4}{5}e^{5x} + C\)

Part D: Logarithmic Integral

The Missing Case: \(n = -1\)

Recall the power rule:

\[\int x^n \, dx = \frac{x^{n+1}}{n+1} + C \quad \text{for } n \neq -1\]

Why not \(n = -1\)? Division by zero!

\[\int x^{-1} \, dx = \int \frac{1}{x} \, dx = \text{???}\]

\[\int \frac{1}{x} \, dx = \ln|x| + C\]

Why the Absolute Value?

• Recall: \(\frac{d}{dx}[\ln x] = \frac{1}{x}\) (for \(x > 0\))
• But what about \(x < 0\)?
• For \(x < 0\): \(\frac{d}{dx}[\ln(-x)] = \frac{1}{-x} \cdot (-1) = \frac{1}{x}\)

\[\int \frac{1}{x} \, dx = \ln|x| + C\]

The absolute value handles both positive and negative \(x\).

Examples: Logarithmic Integrals

Example 1: \(\int_1^e \frac{1}{x} \, dx\)

• \(\ln e - \ln 1 = 1 - 0 = 1\)

Example 2: \(\int_1^4 \frac{3}{x} \, dx\)

• \(3(\ln 4 - \ln 1) = 3\ln 4\)

Example 3: \(\int_{-3}^{-1} \frac{2}{x} \, dx\)

• \(2(\ln 1 - \ln 3) = -2\ln 3\)

Summary: Special Integrals

Function	Antiderivative
\(e^x\)	\(e^x + C\)
\(e^{ax}\)	\(\frac{1}{a}e^{ax} + C\)
\(\frac{1}{x}\)	\(\ln|x| + C\)
\(\frac{1}{ax+b}\)	\(\frac{1}{a}\ln|ax+b| + C\)

These formulas will appear frequently in business applications!

Guided Practice - 20 Minutes

Set A: Area Calculations

Work individually for 8 minutes

1. Find the area under \(f(x) = 3x^2\) from \(x = 1\) to \(x = 4\).

2. Find the total area between \(f(x) = x - 3\) and the x-axis from \(x = 0\) to \(x = 5\).

3. Find the total area between \(f(x) = x^2 - 1\) and the x-axis from \(x = 0\) to \(x = 2\).

Set B: Exponential & Logarithmic

Work individually for 6 minutes

1. \(\int e^{4x} \, dx\)

2. \(\int 5e^{-x} \, dx\)

3. \(\int_0^2 e^{3x} \, dx\)

4. \(\int_1^5 \frac{2}{x} \, dx\)

5. \(\int (e^x + \frac{1}{x}) \, dx\)

Practice Set C: Mixed Problems

Work in pairs for 6 minutes

1. Find the area enclosed between \(f(x) = e^x\) and the x-axis from \(x = 0\) to \(x = 2\).

2. A population decays according to \(P(t) = 1000e^{-0.1t}\). Find the average population from \(t = 0\) to \(t = 10\). (Hint: Average = \(\frac{1}{b-a}\int_a^b f(x) \, dx\))

Coffee Break - 15 Minutes

Part E: Business Applications

Total Profit Over Time

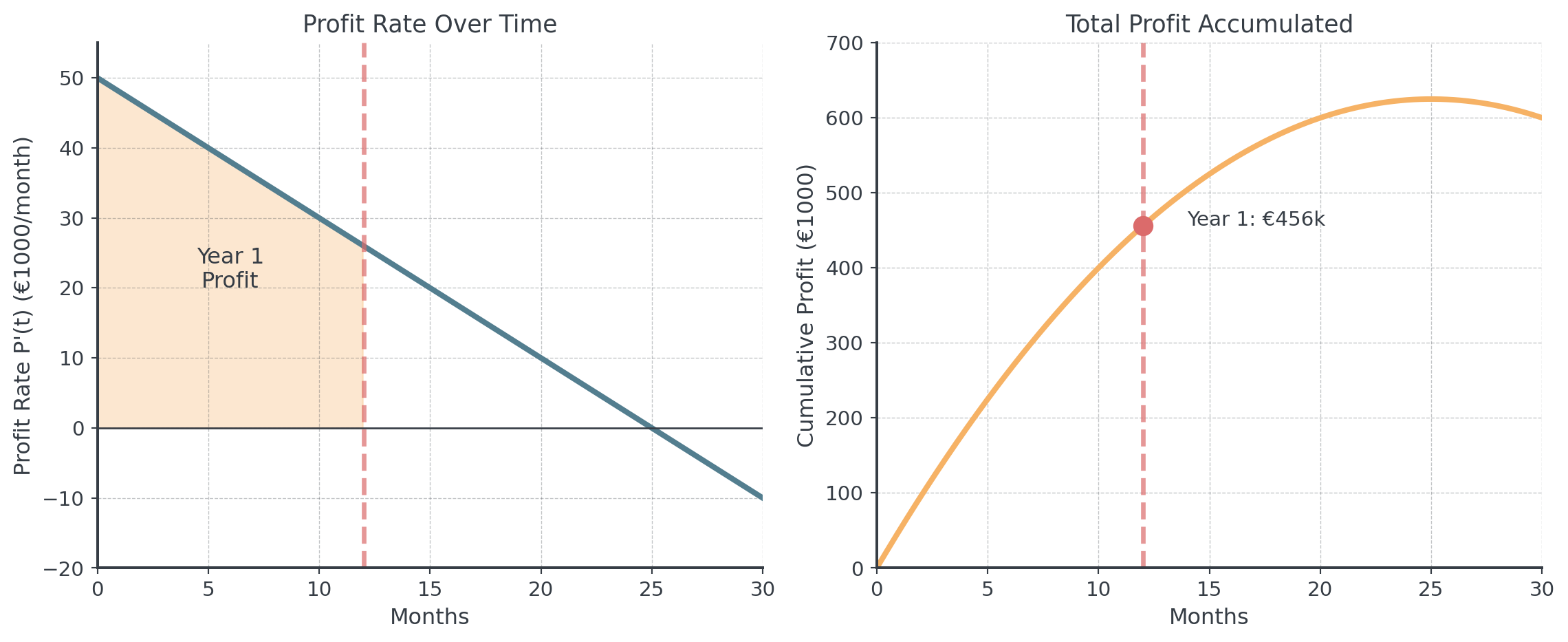
Scenario: A company’s profit rate (profit per month) is:

\[P'(t) = 50 - 2t \text{ thousand euros per month}\]

where \(t\) is months since launch.

Questions:

1. What is the total profit during the first year (\(t = 0\) to \(t = 12\))?
2. At what month does profit rate become negative?

Solution: Profit Analysis

Part 1: Total profit

\[\int_0^{12} (50 - 2t) \, dt = [50t - t^2]_0^{12} = 600 - 144 = 456\]

Total profit = €456,000

Part 2: When profit rate becomes zero

\[50 - 2t = 0 \implies t = 25 \text{ months}\]

The profit rate stays positive for the first 25 months.

Visualizing Profit Accumulation

Exponential Decay in Business

Scenario: Sales of a product decline exponentially after its peak:

\[S(t) = 10000 \cdot e^{-0.2t} \text{ units per month}\]

Question: What are the total sales from \(t = 0\) to \(t = 6\) months?

Solution:

\[\int_0^6 10000e^{-0.2t} \, dt = 10000 \cdot \frac{1}{-0.2}e^{-0.2t}\Big|_0^6\]

\[= -50000(e^{-1.2} - e^0) = -50000(0.301 - 1) = 34,950 \text{ units}\]

Collaborative Problem-Solving - 30 Minutes

Group Challenge: Market Analysis

Scenario: An e-commerce company tracks its daily revenue rate:

\[R'(t) = 5000 + 200t - 5t^2 \text{ euros per day}\]

where \(t\) is days since a marketing campaign started.

The campaign runs for 30 days.

Group Tasks

Work in groups of 3-4

1. Graph \(R'(t)\) for the 30-day period. When is the revenue rate highest?

2. Calculate the total revenue for the first 10 days.

3. Calculate the total revenue for the entire 30-day campaign.

4. On which day does the revenue rate first drop below €4,000/day?

5. Find the average daily revenue rate over the 30-day campaign.

6. If the campaign costs €80,000, what is the net profit?

Wrap-Up & Key Takeaways

Today’s Essential Concepts

• Area under curve when \(f(x) \geq 0\): Use \(\int_a^b f(x) \, dx\) directly
• Total area: Split at zeros and sum absolute values
• Exponential integrals: \(\int e^{ax} \, dx = \frac{1}{a}e^{ax} + C\)
• Logarithmic integral: \(\int \frac{1}{x} \, dx = \ln|x| + C\)
• Business applications: Total quantities from rate functions
• Average value: \(\frac{1}{b-a}\int_a^b f(x) \, dx\)

Next session: Area between TWO curves and economic surplus!

Final Assessment - 5 Minutes

Quick Check

Work individually, then compare

1. Find the total area between \(f(x) = x - 2\) and the x-axis from \(x = 0\) to \(x = 4\).

2. Evaluate \(\int_0^3 2e^{-x} \, dx\).

3. A company’s revenue rate is \(R'(t) = 100 + 20t\) thousand euros per month. Find total revenue for months 1-5.

Next Session Preview

Coming Up: Area Between Curves

• Finding intersection points of two functions
• Determining which function is “on top”
• Setting up \(\int_a^b [f(x) - g(x)] \, dx\)
• Handling multiple regions
• Consumer and producer surplus introduction

Complete Tasks 06-03

• Practice area calculations with sign changes
• Work with exponential and logarithmic integrals
• Focus on business rate-to-total problems