Session 05-02 - The Derivative as Rate of Change
Section 05: Differential Calculus
Entry Quiz - 10 Minutes
Quick Review from Session 05-01
Test your understanding of limits and continuity
Evaluate: \(\lim_{x \to 3} \frac{x^2 - 9}{x - 3}\)
For \(f(x) = \begin{cases} x^2 & \text{if } x < 2 \\ 4 & \text{if } x = 2 \\ 2x & \text{if } x > 2 \end{cases}\), is \(f\) continuous at \(x = 2\)?
A taxi charges €5 for trips up to 5km, then €8 for trips over 5km. Is the cost function continuous at 5km?
If \(\lim_{x \to a} f(x) = L\), must \(f(a) = L\)? Explain.
Homework Discussion - 15 Minutes
Your questions from Session 05-01
What questions do you have regarding the tasks?
Learning Objectives
What You’ll Master Today
- Understand rate of change as slope between points
- Develop the derivative from average to instantaneous rates
- Master derivative notation and terminology
- Apply marginal analysis to business decisions
- Interpret derivatives in economic contexts
Today’s Big Idea
The derivative measures how things change right now, the instantaneous rate of change. This is the foundation of all calculus!
Part A: Average Rate of Change
Slope Review
Remember from linear functions: slope measures rate of change.
- Formula: \(m = \frac{\text{rise}}{\text{run}} = \frac{y_2 - y_1}{x_2 - x_1}\)
- Interpretation: How much \(y\) changes per unit change in \(x\)
- Business meaning: Rate of growth, cost per unit, etc.
Question:If revenue increases from €1000 to €1500 when production goes from 10 to 15 units, by how much does revenue increase per additional unit?
Revenue increases by €100 per additional unit.
Average Rate of Change
For ANY function (not just linear), we can measure average change:
Average Rate of Change from \(a\) to \(b\): \[\text{ARC} = \frac{f(b) - f(a)}{b - a}\]
- This is the slope of the secant line through \((a, f(a))\) and \((b, f(b))\)
- Tells us the average change over an interval
- For linear functions, ARC is constant
- For nonlinear functions, ARC varies by interval
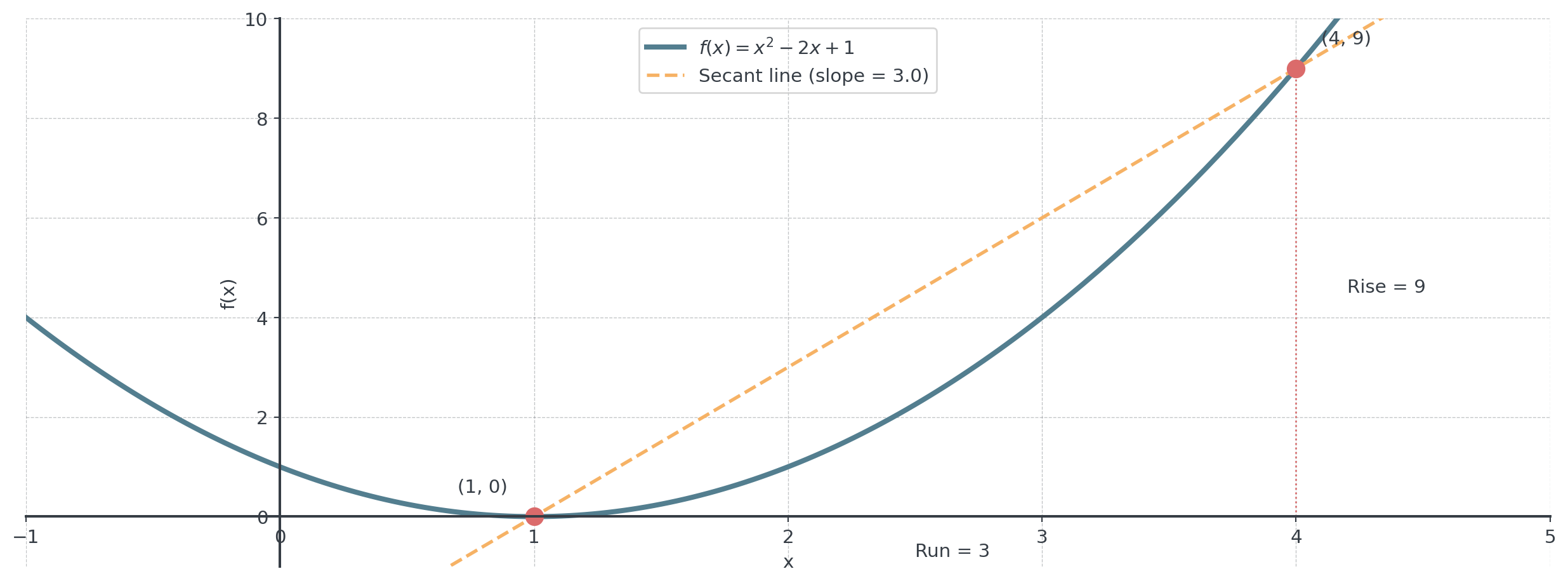
Visual: Secant Line
Average rate of change from \(x=1\) to \(x=4\) is 3 (the slope of the secant line).
Business Example: Revenue Growth
A company’s monthly revenue (in €1000s): \(R(t) = 2t^2 + 5t + 10\).
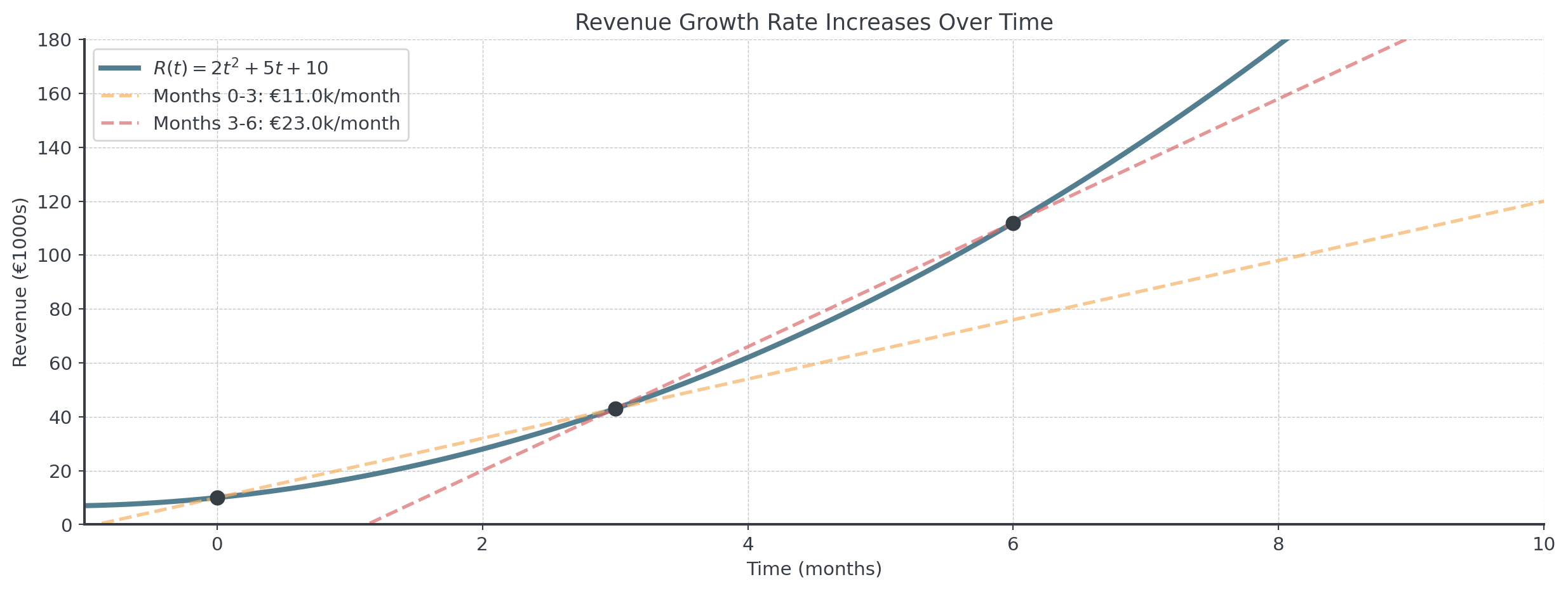
Notice: Revenue grows faster in later months (steeper secant line)!
Quick Practice - 10 Minutes
Calculate Average Rates
Work individually for 5 minutes
For \(f(x) = x^2 + 3x\):
Find the average rate of change from \(x = 1\) to \(x = 3\)
Find the average rate of change from \(x = 1\) to \(x = 2\)
Find the average rate of change from \(x = 1\) to \(x = 1.5\)
What pattern do you notice as the interval gets smaller?
Break - 10 Minutes
Part B: Instantaneous Rate of Change
The Limit Process
What if we want the rate of change at a single point?
- Average rate needs TWO points
- At ONE point, there’s no interval to measure over
- Solution: Make the interval infinitesimally small!
- Use limits to let the second point approach the first
Instantaneous Rate of Change at \(x = a\): \(\lim_{h \to 0} \frac{f(a + h) - f(a)}{h}\)
This limit (if it exists) is called the derivative of \(f\) at \(a\).
Visual: Secant Becoming Tangent
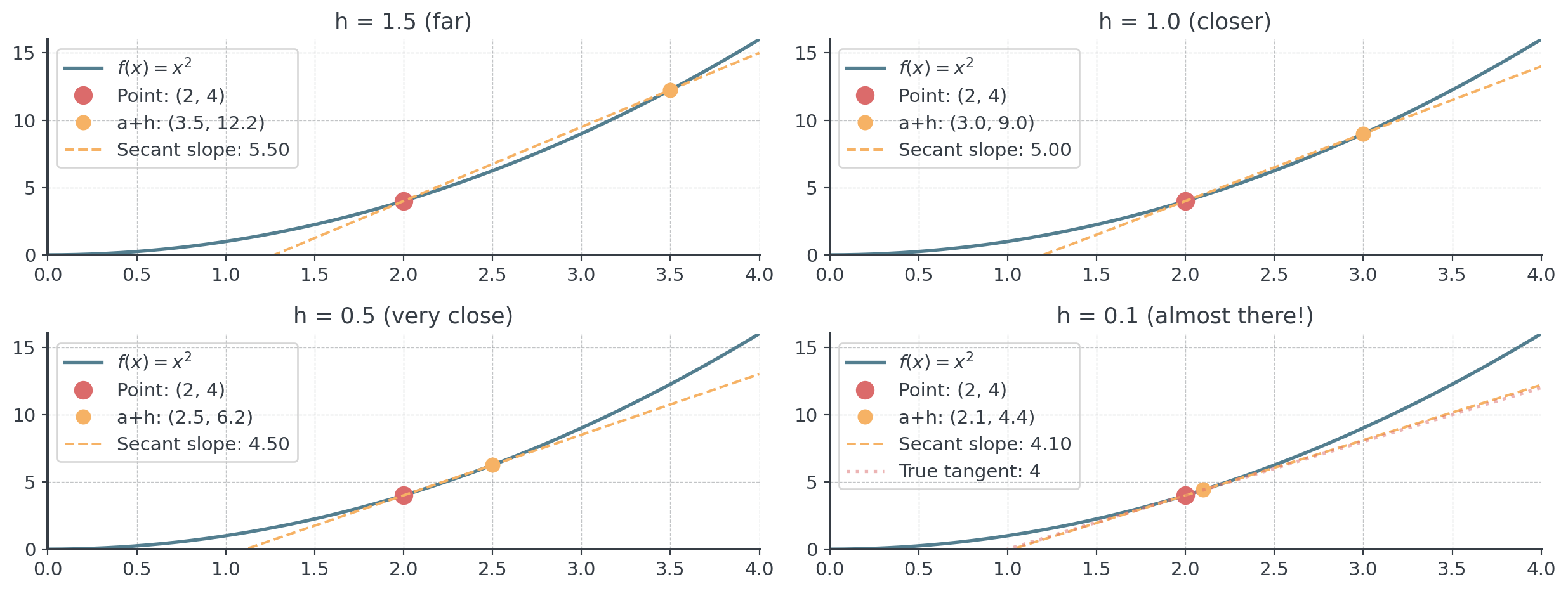
As \(h \to 0\), the secant line approaches the tangent line!
The Derivative Definition
The derivative of \(f\) at \(x = a\) is: \[f'(a) = \lim_{h \to 0} \frac{f(a + h) - f(a)}{h}\]
- Geometric meaning: Slope of the tangent line at \((a, f(a))\)
- Physical meaning: Instantaneous rate of change
- Verbal: “f prime of a” or “the derivative of f at a”
The derivative is the LIMIT of average rates of change, not just “a very small” average rate!
Computing Derivative from Definition
Example: Find \(f'(2)\) if \(f(x) = x^2\).
Definition: \(f'(2) = \lim_{h \to 0} \frac{f(2 + h) - f(2)}{h}\)
Substitute: \(= \lim_{h \to 0} \frac{(2+h)^2 - 4}{h}\)
Expand & factor: \(= \lim_{h \to 0} \frac{4h + h^2}{h} = \lim_{h \to 0}(4 + h)\)
Evaluate: \(= 4\) → The tangent slope at \(x = 2\) is 4
Not too complicated, right?
Part C: Derivative Notation & Terminology
The Derivative as a Function
When \(f'(x)\) (not \(f'(a)\)), we mean the derivative at ANY point \(x\):
\[f'(x) = \lim_{h \to 0} \frac{f(x + h) - f(x)}{h}\]
- This defines a NEW function \(f'\) from the original function \(f\)
- \(f'(x)\) gives the slope of the tangent at each \(x\)
Example: If \(f(x) = x^2\), then \(f'(x) = 2x\) (we’ll prove this soon!)
- At \(x = 1\): slope is \(2(1) = 2\) and at \(x = 3\): slope is \(2(3) = 6\)
- The function gets steeper as \(x\) increases
Multiple Notations
There are several ways to write “the derivative of \(f\) at \(x\)”:
| Notation | Read as | Context |
|---|---|---|
| \(f'(x)\) | “f prime of x” | Function notation |
| \(\frac{df}{dx}\) | “derivative of f with respect to x” | Leibniz notation |
| \(\frac{dy}{dx}\) | “dy dx” | When y = f(x) |
| \(\frac{d}{dx}[f(x)]\) | “d dx of f of x” | Operator notation |
We’ll primarily use \(f'(x)\) for general work and \(\frac{dy}{dx}\) when emphasizing the variables.
Differentiability vs Continuity
Not every function has a derivative everywhere!
- If \(f'(a)\) exists, we say \(f\) is differentiable at \(a\)
- Theorem: If \(f\) is differentiable at \(a\), then \(f\) is continuous at \(a\)
- Converse is false: Continuous functions may not be differentiable
Question: Ever hear the word Theorem before?
A Theorem is basically a statement that has been proven to be true.
Continuous but not differentiable
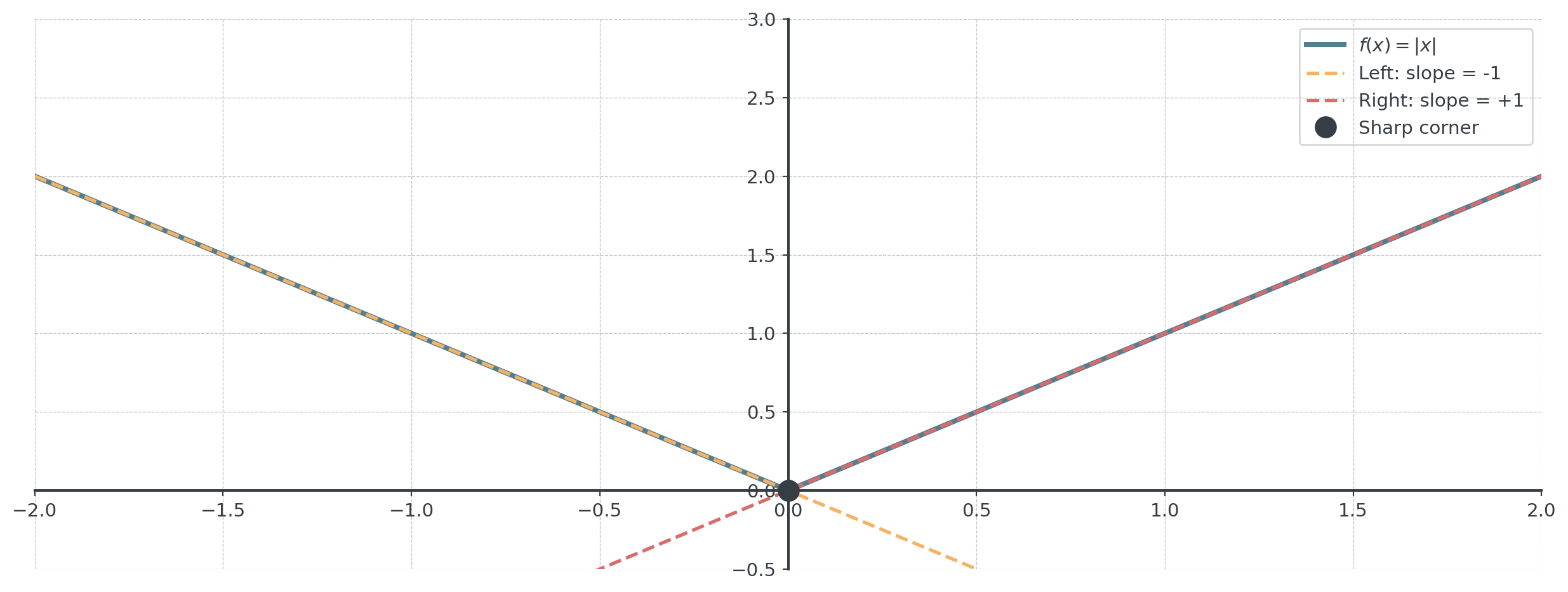
At \(x = 0\), the limit doesn’t exist (left and right slopes differ).
Practice: Derivatives from Definition
Work in pairs for 15 minutes
Use the limit definition to find \(f'(a)\) at the given point:
\(f(x) = 3x + 2\) at \(a = 1\)
\(f(x) = x^2 - 4x\) at \(a = 3\)
\(f(x) = \frac{1}{x}\) at \(a = 2\)
Interpret each derivative: what does the value tell you?
Coffee Break - 15 Minutes
Part D: Marginal Analysis in Economics
The Marginal Concept
In economics, “marginal” means “the next one”:
- Marginal cost: Cost of producing one more unit
- Marginal revenue: Revenue from selling one more unit
- Marginal profit: Profit from one more unit
Question: How can we apply this now with what we’ve learned?
The derivative tells us the instantaneous rate of increase in cost per unit of production.
Why Derivatives Give Marginal Values
True marginal cost at \(x = 100\) units: \[MC(100) = C(101) - C(100)\]
But this is approximately: \[C'(100) = \lim_{h \to 0} \frac{C(100 + h) - C(100)}{h}\]
When \(h = 1\) (one more unit), the approximation is very good: \[C'(100) \approx \frac{C(101) - C(100)}{1} = C(101) - C(100)\]
Example: Marginal Cost
A factory’s total cost function is: \(C(x) = 1000 + 5x + 0.01x^2\).
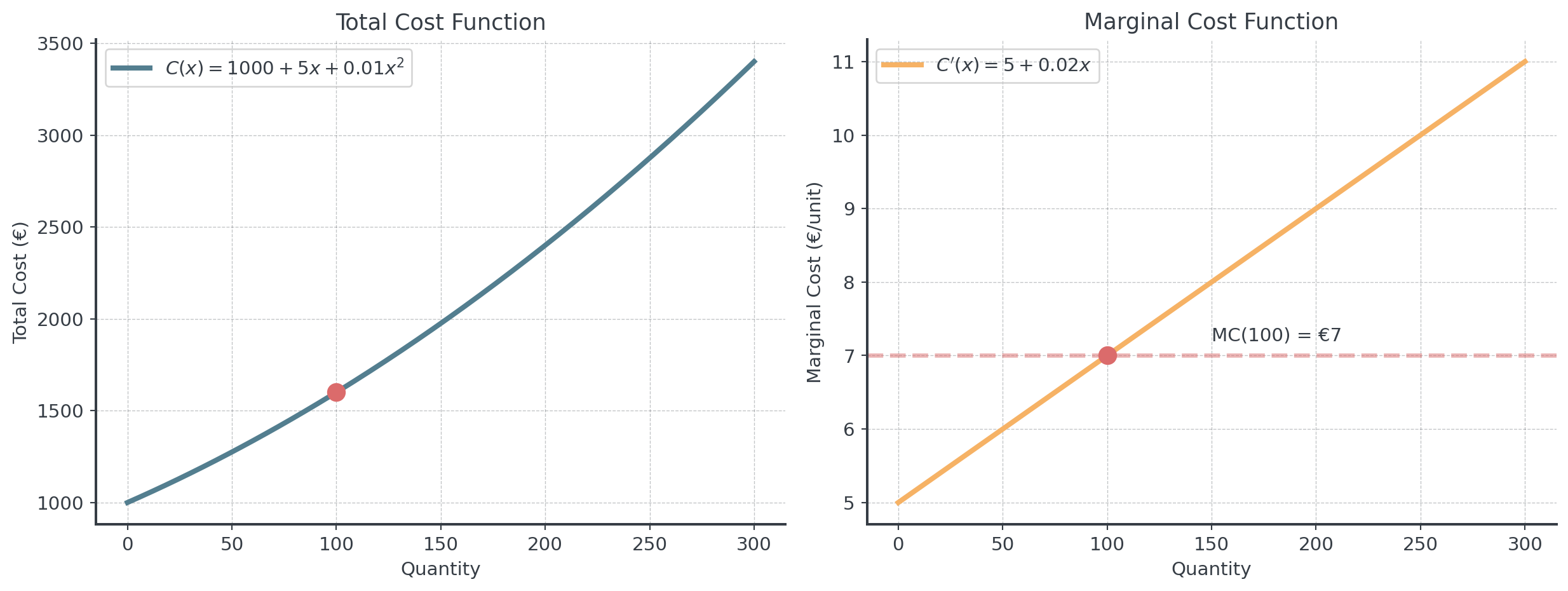
\(MC(100) = C'(100) = 5 + 0.02(100) = €7\) per unit
Marginal Revenue
Revenue: \(R(x) = x \cdot p = x(100 - 0.5x) = 100x - 0.5x^2\)
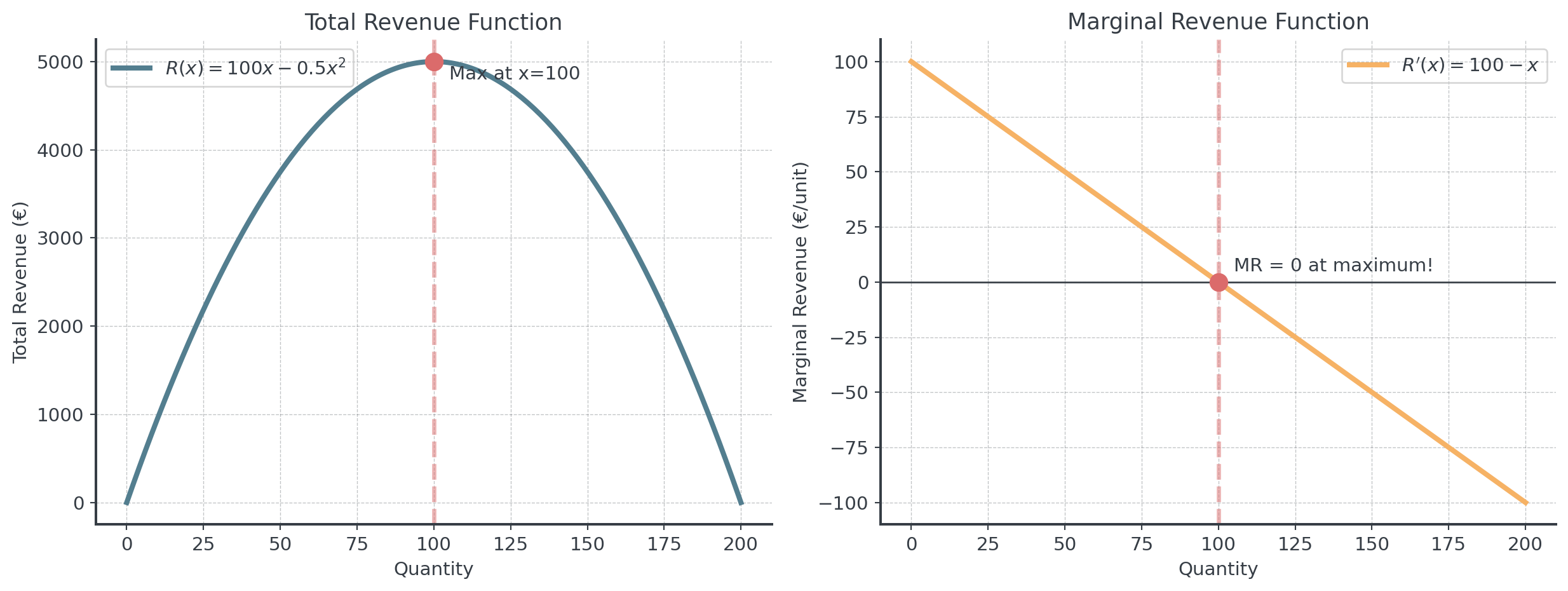
Revenue is maximized when \(MR = 0\)!
Marginal Profit
Since \(P(x) = R(x) - C(x)\), we have:
\[P'(x) = R'(x) - C'(x)\]
Interpretation: Marginal profit = Marginal revenue − Marginal cost
- Produce more if \(MR > MC\) (next unit adds more revenue than cost)
- Produce less if \(MR < MC\) (next unit costs more than it earns)
- Optimal: \(MR = MC\) (marginal revenue equals marginal cost)
Makes sense, right? Profit is maximized when \(MR = MC\)!
Practice Set: Marginal Analysis I
Work for 5 minutes
Use the given derivatives to answer each question:
- Cost function \(C(x) = 500 + 3x + 0.02x^2\)
- Given: \(C'(x) = 3 + 0.04x\)
- Calculate \(C'(50)\) and interpret what it means for the business
- Revenue function \(R(x) = 80x - 0.5x^2\)
- Given: \(R'(x) = 80 - x\)
- At what quantity does \(R'(x) = 0\)? What does this mean?
Practice Set: Marginal Analysis II
Work for 5 minutes
Use the given derivatives to answer each question:
- Given: \(P'(x) = R'(x) - C'(x) = 77 - 1.04x\)
- What production level maximizes profit (set \(P'(x) = 0\))?
- Interpretation: If \(C'(100) = 7\) and \(R'(100) = 5\), should the company increase or decrease production?
Collaborative Problem-Solving
Coffee Shop Economics
A coffee shop’s daily profit depends on the number of drinks sold: \[P(x) = -0.02x^2 + 8x - 200\]
where \(x\) is the number of drinks and \(P\) is profit in euros.
Find the average rate of change of profit from 100 to 150 drinks.
Estimate \(P'(150)\) by computing \(\frac{P(151) - P(150)}{1}\).
Interpret: What does \(P'(150)\) tell the shop owner?
Determine: Should they try to sell more than 150 drinks?
Find where \(P'(x) = 0\) by solving \(8 - 0.04x = 0\).
Explain the business significance of the point where \(P'(x) = 0\).
Think-Pair-Share
Conceptual Question
Think → Discuss → Share
Question: A company finds that \(C'(500) = 12\) and \(R'(500) = 15\).
What should they do?
- Increase production
- Decrease production
- Keep production at 500 units
Explain your reasoning using marginal analysis.
Wrap-Up & Key Takeaways
Today’s Essential Concepts
- Average rate of change is the slope of a secant line
- Instantaneous rate is the limit as the interval shrinks to zero
- The derivative \(f'(a) = \lim_{h \to 0} \frac{f(a+h) - f(a)}{h}\)
- Marginal analysis: Derivatives give marginal cost, revenue, profit
- Optimization: Maximize profit where \(MR = MC\) (where \(P'(x) = 0\))
The derivative is THE fundamental tool in calculus. It measures instantaneous rate of change. It tells us how things are changing right now!
Final Assessment
Quick Check
Work individually, then we discuss
If \(f(3) = 7\) and \(f(3.1) = 7.5\), estimate \(f'(3)\).
A cost function has \(C'(200) = 8\). What does this tell you?
For profit maximization, we set _______ = _______.
True or False: If a function is continuous at \(x = a\), it must be differentiable at \(x = a\).
Next Session Preview
Coming Up
Differentiation Rules
- Power rule, sum rule, constant multiple rule
- Product and quotient rules
- Finding equations of tangent lines
- More business applications
- NO MORE tedious limit calculations!
Complete Tasks 05-02!
Session 05-02 - The Derivative as Rate of Change | Dr. Nikolai Heinrichs & Dr. Tobias Vlćek | Home